Аксиома эскобара что это такое

Bredor — Lurkmore

Журналистка: — Всё, да? Перед вами группа Bredor. Представьтесь. Влад: — Я Влад. Журналистка: — На чём ты играешь? Влад: — (долго пытается вспомнить) Играю на бас-гитаре. Эскобар: — Я Эскобар. Журналистка: — (неразборчиво) Да можно и ничего больше. Валера: — (кокетливым голосом) М-м-м, а я Валера. Коля: — А я Коля, на барабанах. Эскобар: (что-то говорит про кокаин). Журналистка: — Ребят, а как давно вы образовались, и почему именно Бредор? (длительная пауза) Эскобар: — Шо? Журналистка: — Почему группа называется именно Бредор? Эскобар: — А ну хер его знает, ну Бредор, мля, ну Бредор… Валера: — Да, Бредор — это короче как бы… Это, так сказать, своё мировоззрение. (обращаясь к Эскобару) — Заголи им, покажи, блядь. Печать. (усмехается) Эскобар: — Печать. У меня на члене в-о-о-т такая печать. Я те, если хочешь, могу потом после интервью показать, индивидуально. (смеётся) Журналистка: — Ну хорошо, тогда скажи мне, пожалуйста, как давно ты в себе обнаружил такой вокальный… такие вокальные данные? Эскобар: (указывая на татуировку на плече) — Это он, он обнаружил, он обнаружил. В семи вокалах, мля… пою, нехуй делать. Могу и так, знаешь, и сяк. Вообще, чё вы всё у меня вопросы задаёте, вы спра… Журналистка: — Ну ты как лидер, я тебе и задаю вопросы… (запись прерывается белым шумом) Эскобар: — …ского подсознания. Журналистка: — А кто пишет тексты песен? Эскобар: — Пишет техсты нам нихто. Техсты у нас чисто сугубо психологические и возникают спонтанно. Ну это… это не есть, то есть сказать, музыка, это данный этап, так называемая эйфория. Ну, поддерживаемая наркотическими веществами там. Ну самое лучшее — это использовать морфина гидрохлорид пятипроцентный раствор. Потому что он как бы тонизирует человеческий организм, подстёгивает его психо… психику. Ну и дело в том что, видите, оно даже когда, например, выступаешь в таких, пронизанных сплошь и рядом, таким, опиумным дурмано́м молодых лиц, то оно, например, видно сразу, шо там чем отличается от чего. Валера: — Это на ... (неразборчиво) Журналистка: — А чувствуется разница между «Бомбером» и, допустим, этим концертом? Эскобар: — Шо то хуйня, шо это хуйня. Вот это обе хуйни такие, шо я, бля, ебал её маму у рот. Это можете вырезать полностью, блядь, этот камера нахуй. То шо, бля… Журналистка: — Спасибо… (собирается уйти, но Эскобар ее останавливает) Эскобар: — Не, я ещё пару слов. То... то, шо вот это вот, вот это, я вообще охеревший, шо это, блядь, такое, нахуй? В натуре! У на... у нас на репетиции вот так чуваки приходят поугорать, блядь. О, блядь! Ум-да, бля, ум-да, (изображая игру на гитаре) ти-ри-ри-ри-ри-ри… зироу хироу, зиро хиро…

Теорема или Аксиома Эскобара- что это?

Теорема Эскобара (она же аксиома Эскобара) – популярный в сети мем, обычно используемый в различных спорах участником, который не хочет принимать ни одну из сторон.
В чем суть аксиомы Эскобара? Выражение означает ситуацию, когда человеку предложен выбор между двумя крайностями – в этом случае, по мнению автора оригинальной фразы, оба варианта не стоят внимания.
Практически аксиому Эскобара иногда применяют в опросах, добавляя к двум вариантам ответа третий – “Эскобар”.
Распространение в интернете аксиома Эскобара получила после публикации статьи на эту тему на Лурке, ныне закрытом для просмотра Роспотребнадзором.

Теоремой Эскобара можно назвать фразу, которая была взята из репортажа о лидере украинской рок-музыкальной группы «Bredor» во главе Эскобара.

Примерно в 90х годах зародилась группа бредор, которая в скором времени обрела свою популярность за счёт скандальных жанров музыки. Они пели от психодилеческих песен до грайндкора и брутала. Чуть позже они начали уже организовывать свои выступления и после небольшого концерта им предложили записать интервью, что и сделало их популярными. Интервью сразу же попало в интернет, где получило тонну смешных комментариев в их адрес.
Данные люди не зря писали в психоделическом формате, т.к были любителями употреблять различные наркотики, которые, к слову, из их интервью «тонизировали и помогали написать музыку». Всё это звучит конечно странно, но данный случай был очень весёлым. Даже когда у них брали интервью, то некоторые участники группы пребывали не совсем адекватном состоянии и просто не могли вести диалог, вероятнее всего из-за наркотических веществ, которые они часто употребляли перед концертами. Теорема попала в интернет в 2007 году, хотя, из данного интервью было и много других моментов. Вот сама фраза: при безальтернативном выборе противоположных сущностней обе будут являть собой исключительную х***ю.

Копирование информации с сайта greednews.su разрешено только при использовании активной гипер ссылки на новость, спасибо за то что цените н

«АКСИОМА ЭСКОБАРА» КАК ОСНОВА СОВРЕМЕННОГО УКРАИНСКОГО ПОЛИТИЧЕСКОГО ДИСКУРСА

В цензурном варианте эта аксиома звучит так: «При безальтернативном выборе из двух противоположных сущностей обе будут являть собой исключительную херню».

В нецензурном – звучит еще более правдиво и отлично ложится на ситуацию с выборами-2019: насчет власти и оппозиции.

Однако же, в некотором смысле эта безальтернативность может облегчить нам жизнь. По крайней мере, на метафизическом уровне. Попытаюсь объяснить.

Я не раз писала, что счастье свидомых в том, что они тупые.
А у нас – классическое «горе от ума».

Мы критически осмысливаем реальность, стараясь читать умные книжки, помнить уроки историю, устанавливать причинно-следственные связи, искать логическое обоснование, анализировать разные точки зрения, пытаться предвидеть последствия… И все у нас отлично получается на уровне «потрындеть в фейсбучике».

А в реальной жизни каждый свидомый имеет полное право задать нам вопрос «Ну, и шо цэ тоби дало?» И у нас нет на него ответа.

И сейчас в ходе предвыборной гонки вся лента в информации о том, что голосовать не за кого, оппозиция бутафорская, Мураев слишком мутный, Вилкул слишком прозрачный, Добкин какой-то несерьезный, Новинский – слишком серьезный, Медведчук – слишком темная лошадка, а Бойко – слишком светлая. И тагдалие.

И все-то мы анализируем, и все то мы про них помним, и все-то мы про них понимаем. Мы умные и нас не проведешь!

А у свидомых все просто – кандыдат у вышыванцыи? Всьо, голосует!

Остальное неважно.

Обещает уже завтра жизнь как в Швейцарии? Всьо, бежит, только шаровары мелькают. И даже парализованную бабушку тащит на избирательный участок.

Потому, что в их тупости их счастье.

И их сила.

А мы же пытаемся играть в шахматы с голубем, тщательно продумывая ходы и рокировки.

Они не зморачиваются чтением политических биографий кандидатов, их экономических программ, не анализируют, что было выполнено из предыдущих предвыборных обещаний, не связывают в одну логическую цепочку нынешнюю власть и теперешнее тотальное обнищание, не видят никаких минусов, если кандидат – «патриот» и красиво обещает. Иногда мне кажется, что если кто-то нассыт свидомому на лицо, но при этом будет украиноязычным и в вышыванке, то он и в этом случае найдет оправдание ссавшему. Этим и объясняется, что после стольких лет пустых надежд, свидомые все еще продолжают голосовать за «патриотив». Но это так, к слову.

На самом же деле, то, что в течение последних 5 лет помогало нам сохранить здравый смысл, сейчас, как это не странно, работает против нас. Мы видим все минусы, все слабые места, все косяки оппозиции, но главная проблема в том, что альтернативы им нет. Вот просто нет, и все. Аксиома Эскобара.

Поэтому, ребята, ау! Нет на горизонте никакого Че Гевары. И в обозримом будущем не предвидится.

И никто из нынешних политиков за счастье трудового народа и офисной интеллигенции сражаться не собирается. Это капитализм, детка.

Выбор сегодня на Украине стоит всего лишь между «жить очень херово» и «жить просто херово». Но и этот выбор хорошо бы не прое... не прощелкать. И сейчас, и на парламентских выборах.

В ходе прыжков на майдане мы отпрыгнули настолько далеко от цивилизации, что ни следующая власть, ни последующая не сможет преодолеть эту пропасть.

Максимум, повторяю – максимум! – это слегка затормозить падение, если не в экономической, то хотя бы в идеологической сфере. И для этого сгодится любой условный мураевовилкуломедведчук. Это с одной стороны.

А с другой – даже колония грибов или мух дрозофил сможет лучше управлять Украиной, чем те политики, которые сейчас у нас при власти. Хотя бы поэтому надо дать оппозиции шанс.

Да, есть риск, что выбранные нами политики не оправдают оказанного им доверия. Здесь, как в анекдоте про блондинку и динозавра – 50 на 50. Или оправдают или нет. А вот нынешняя власть 100% будет продолжать эту убийственную для страны и народа политику узаконенного экономического геноцида и эскалации гражданского противостояния.

Поэтому лично для меня безальтернативность выбора означает лишь одно: надо идти и голосовать за оппозицию. За ту, которая есть. За ту, которая единственно возможна в ситуации тотальной зачистки инакомыслящих. За ту, которая дает хоть какой-то призрачный шанс.

По большому счету, наш голос – не столько « за», сколько «против».

Против нынешней власти.

А грядущие выборы не столько выборы, сколько перепись нормальных людей. И очень хочется узнать, сколько же нас на самом деле.

Бэлла Розенфельд (Марина Соловьева)

Аксиома выбора — Википедия

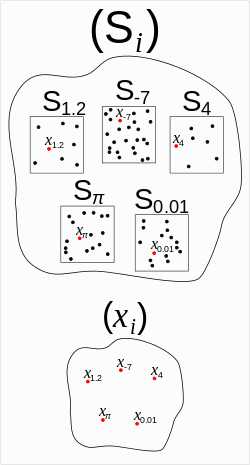Где (S_i) семейство непустых множеств, проиндексированных множеством действительных чисел R. То есть для каждого действительного числа i существует множество S_i. На рисунке приведен пример выбора элементов множеств. Каждое такое множество S_i непусто, а возможно и бесконечно. Аксиома выбора позволяет нам произвольно выбирать один элемент из каждого множества, формируя соответствующее семейство элементов (x_i), также проиндексированных множеством действительных чисел R, где x_i выбраны из S_i.

Аксиомой выбора, англ. аббр. AC (от axiom of choice) называется следующее высказывание теории множеств:

Для всякого семейства^[1]X{\displaystyle X} непустых множеств существует функция f{\displaystyle f}, которая каждому множеству семейства сопоставляет один из элементов этого множества^[2]. Функция f{\displaystyle f} называется функцией выбора для заданного семейства.

На формальном языке:

∀X[∅∉X⇒∃f:X→⋃X∀A∈X(f(A)∈A)].{\displaystyle \forall X\left[\emptyset \notin X\Rightarrow \exists f\colon X\rightarrow \bigcup X\quad \forall A\in X\,(f(A)\in A)\right]\,.}

Если мы ограничимся рассмотрением только конечных семейств множеств, то утверждение аксиомы выбора может быть доказано исходя из других аксиом теории множеств^[2] и не требует постулирования в качестве отдельной аксиомы. Оно также может быть доказано для некоторых бесконечных семейств, однако в общем случае для бесконечных семейств аксиома выбора не следует из других аксиом и является независимым утверждением.

Аксиома выбора была сформулирована и опубликована Эрнстом Цермело в 1904 году (хотя впервые её отметил Беппо Леви на 2 года раньше). Новая аксиома вызвала бурную полемику и до сих пор не все математики принимают её безоговорочно^[3]. Высказывались мнения, что доказательства, полученные с её привлечением, имеют «иную познавательную ценность», чем доказательства, не зависящие от неё^[3]^[4]. Появление аксиомы выбора вызвало также дискуссию о том, что означает в математике понятие «существование» — в частности, о том, можно ли считать существующим множество, ни один элемент которого не известен.^{[источник не указан 30 дней]}

Неприятие аксиомы выбора некоторыми} математиками обосновано, прежде всего, тем, что в ней лишь утверждается существование множества d{\displaystyle d}, но не дается никакого способа его определения; такое мнение высказывали, например, Бореля и Лебега^[4]. Противоположного мнения придерживались, например, Гильберт, Хаусдорф и Френкель, которые принимали аксиому выбора без всяких оговорок, признавая за ней ту же степень «очевидности», что и за другими аксиомами теории множеств: аксиома объёмности, аксиома существования пустого множества, аксиома пары, аксиома суммы, аксиома степени, аксиома бесконечности.^{[источник не указан 30 дней]}

Более того, среди следствий аксиомы выбора есть много довольно парадоксальных, вызывающих интуитивный протест части математиков. Например, появляется возможность доказать парадокс удвоения шара, который вряд ли могут счесть «очевидным» все исследователи (см. также Квадратура круга Тарского). Подробный анализ многочисленных доказательств, использующих аксиому выбора, провел Вацлав Серпинский. Однако, без сомнения, многие важные математические открытия нельзя было бы сделать без аксиомы выбора^[5].

Бертран Рассел так отозвался об аксиоме выбора: «Сначала она кажется очевидной; но чем больше вдумываешься, тем более странными кажутся выводы из этой аксиомы; под конец же вообще перестаешь понимать, что же она означает»^[6].

Независимость аксиомы выбора от остальных аксиом Цермело — Френкеля доказал Пол Коэн^[7]^[8].

Существует множество других, эквивалентных формулировок аксиомы выбора.

Функция выбора — функция на множестве множеств X{\displaystyle X} такая, что для каждого множества s{\displaystyle s} в X{\displaystyle X}, f(s){\displaystyle f(s)} является элементом из s{\displaystyle s}. С использованием понятия функции выбора аксиома утверждает:

Для любого семейства непустых множеств X{\displaystyle X} существует функция выбора f{\displaystyle f}, определённая на X{\displaystyle X}.

Или наиболее сжато:

Каждое множество непустых множеств имеет функцию выбора.

Вторая версия аксиомы выбора утверждает:

Для данного произвольного множества попарно непересекающихся непустых множеств существует по крайней мере одно множество, которое содержит точно один элемент, общий с каждым из непустых множеств.

Некоторые авторы используют другую версию, которая эффективно утверждает:

Для любого множества A{\displaystyle A}, его булеан за вычетом пустого подмножества P(A)∖{∅}{\displaystyle {\mathcal {P}}(A)\setminus \{\varnothing \}} имеет функцию выбора.

Авторы, которые используют эту формулировку, часто также говорят о «функции выбора на A{\displaystyle A}», но оговаривают, что имеют в виду немного другое понятие функции выбора. Её область определения — булеан (минус пустое подмножество), тогда как в других местах этой статьи, область определения функции выбора — «множество множеств». С этим дополнительным понятием функции выбора, аксиома выбора может быть сжато сформулирована так:

Каждое множество имеет функцию выбора.

До конца XIX века аксиома выбора использовалась безоговорочно. Например, после определения множества X{\displaystyle X}, содержащего непустое множество, математик мог сказать: «Пусть F(s){\displaystyle F(s)} будет определено для каждого s{\displaystyle s} из X{\displaystyle X}». Без аксиомы выбора в общем случае невозможно доказать, что F{\displaystyle F} существует, но это, кажется, оставалось без внимания до Цермело.

Не во всех случаях требуется аксиома выбора. Для конечного набора X{\displaystyle X} аксиома выбора следует из других аксиом теории множеств. В этом случае это то же самое, что говорить, если мы имеем несколько (конечное число) коробок, каждая из которых содержит в себе по одной одинаковой вещи, тогда мы можем выбрать ровно одну вещь из каждой коробки. Ясно, что мы можем сделать это: мы начнём с первой коробки, выберем вещь; отправимся ко второй коробке, выберем вещь; и т. д. Так как есть конечное число коробок, то действуя нашей процедурой выбора, мы придём к концу. Результатом будет функция явного выбора: функция, которая первой коробке сопоставляет первый элемент, который мы выбрали, второй коробке — второй элемент и т. д. (Для получения формального доказательства для всех конечных множеств следует воспользоваться принципом математической индукции.)

В случае с бесконечным множеством X{\displaystyle X} иногда также можно обойти аксиому выбора. Например, если элементы X{\displaystyle X} — множества натуральных чисел. Каждый непустой набор натуральных чисел имеет наименьший элемент, таким образом, определяя нашу функцию выбора, мы можем просто сказать, что каждому множеству сопоставляется наименьший элемент набора. Это позволяет нам сделать выбор элемента из каждого множества, поэтому мы можем записать явное выражение, которое говорит нам, какое значение наша функция выбора принимает. Если возможно таким образом определить функцию выбора, в аксиоме выбора нет необходимости.

Сложности появляются в случае, если невозможно осуществить естественный выбор элементов из каждого множества. Если мы не можем сделать явный выбор, то почему уверены, что такой выбор можно совершить в принципе? Например, пусть X{\displaystyle X} — это множество непустых подмножеств действительных чисел. Во-первых, мы могли бы попробовать поступить как в случае, если бы X{\displaystyle X} было конечным. Если мы попробуем выбрать элемент из каждого множества, тогда, так как X{\displaystyle X} бесконечно, наша процедура выбора никогда не придёт к концу, и вследствие этого мы никогда не получим функции выбора для всего X{\displaystyle X}. Так что это не срабатывает. Далее, мы можем попробовать определить наименьший элемент из каждого множества. Но некоторые подмножества действительных чисел не содержат наименьший элемент. Например, таким подмножеством является открытый интервал (0,1){\displaystyle (0,\;1)}. Если x{\displaystyle x} принадлежит (0,1){\displaystyle (0,\;1)}, то x/2{\displaystyle x/2} также принадлежит ему, причем меньше, чем x{\displaystyle x}. Итак, выбор наименьшего элемента тоже не работает.

Причина, которая позволяет выбрать нам наименьший элемент из подмножества натуральных чисел — это факт, что натуральные числа обладают свойством вполнеупорядоченности. Каждое подмножество натуральных чисел имеет единственный наименьший элемент в силу естественной упорядоченности. Может быть, если бы мы были умнее, то могли бы сказать: «Возможно, если обычный порядок для действительных чисел не позволяет найти особое (наименьшее) число в каждом подмножестве, мы могли бы ввести другой порядок, который давал бы свойство вполнеупорядоченности. Тогда наша функция сможет выбрать наименьший элемент из каждого множества в силу нашего необычного упорядочивания». Проблема тогда возникает в этом построении вполнеупорядоченности, которая для своего решения требует наличия аксиомы выбора. Иными словами, каждое множество может быть вполне упорядочено тогда и только тогда, когда аксиома выбора справедлива.

Доказательства, требующие аксиомы выбора, всегда неконструктивны: даже если доказательство создаёт объект, невозможно сказать, что же именно это за объект. Следовательно, хоть аксиома выбора позволяет вполне упорядочить множество действительных чисел, это не даёт нам никакой наглядности и конструктивизма в целом. Сама причина, по которой наш вышеуказанный выбор вполне упорядочения действительных чисел был таким для каждого множества X{\displaystyle X}, мы могли явно выбрать элемент из такого множества. Если мы не можем указать, что мы используем вполне упорядоченность, тогда наш выбор не вполне явный. Это одна из причин, почему некоторые математики не любят аксиому выбора (см. также Кризис оснований математики). Например, конструктивистская установка что все существующие доказательства должны быть полностью явными; должно быть возможным построение чего бы то ни было что существует. Они отвергают аксиому выбора потому, что она заявляет существование объекта без описания. С другой стороны, факт — что для доказательства существования используется аксиома выбора — не означает, что мы не сможем совершить построение другим способом.

Принцип вполне упорядочивания (теорема Цермело)[править | править код]

Очень распространённая и удобная формулировка использует понятие вполне упорядоченного множества. Нам потребуется несколько определений, и мы начнём со строгого определения линейного порядка, выражающего знакомую нам идею на языке теории множеств. Напомним, что упорядоченная пара элементов обозначается (x,y){\displaystyle (x,\;y)}, и что декартово произведение множеств X×Y{\displaystyle X\times Y} состоит из всех возможных упорядоченных пар (x,y){\displaystyle (x,\;y)}, где x∈X,y∈Y{\displaystyle x\in X,\;y\in Y}.

Линейным порядком на множестве A{\displaystyle A} называется подмножество декартова произведения R⊆A×A{\displaystyle R\subseteq A\times A}, обладающее следующим свойствами:

Полное: ∀x,y∈A((x,y)∈R∨(y,x)∈R){\displaystyle \forall x,\;y\in A\;((x,\;y)\in R\lor (y,\;x)\in R)}.

Антисимметричное: ∀x,y∈A((x,y)∈R∧(y,x)∈R→y=x){\displaystyle \forall x,\;y\in A\;((x,\;y)\in R\wedge (y,\;x)\in R\to y=x)}.

Транзитивное: ∀x,y,z∈A((x,y)∈R∧(y,z)∈R→(x,z)∈R){\displaystyle \forall x,\;y,\;z\in A\;((x,\;y)\in R\wedge (y,\;z)\in R\to (x,\;z)\in R)}.
Полным порядком на множестве A{\displaystyle A} называется такой линейный порядок, что каждое непустое подмножество X⊆A{\displaystyle X\subseteq A} имеет наименьший элемент.

Принцип полного порядка заключается в том, что любое множество может быть вполне упорядочено.

Например, множество натуральных чисел может быть вполне упорядоченно обычным отношением «меньше или равно чем». С тем же отношением множество целых чисел не имеет наименьшего элемента. В этом случае мы можем собрать целые числа в последовательность (0,−1,1,−2,2,…,−n,n,…){\displaystyle (0,\;-1,\;1,\;-2,\;2,\;\ldots ,\;-n,\;n,\;\ldots )} и сказать, что младшие члены меньше, чем старшие. Очевидно, такое отношение будет полным порядком на целых числах.

Гораздо менее очевидно, что действительные числа, формирующие несчётное множество, могут быть вполне упорядочены.

Лемма Цорна[править | править код]

Если в частично упорядоченном множестве любая цепь (то есть линейно упорядоченное подмножество) имеет верхнюю грань, то всё множество имеет хотя бы один максимальный элемент.

Более формально:

Пусть (P,⩽){\displaystyle (P,\;\leqslant )} — частично упорядоченное множество, то есть, отношение ⩽{\displaystyle \leqslant } — рефлексивно, антисимметрично и транзитивно:

∀x∈Px⩽x;{\displaystyle \forall x\in P\quad x\leqslant x;}

∀x,y∈Px⩽y∧y⩽x→x=y;{\displaystyle \forall x,\;y\in P\;x\leqslant y\land y\leqslant x\to x=y;}

∀x,y,z∈Px⩽y∧y⩽z→x⩽z.{\displaystyle \forall x,\;y,\;z\in P\;x\leqslant y\land y\leqslant z\to x\leqslant z.}
Подмножество S⊂P{\displaystyle S\subset P} называется линейно упорядоченным, если ∀x,y∈Sx⩽y∨y⩽x{\displaystyle \forall x,\;y\in S\;x\leqslant y\lor y\leqslant x}. Элемент u∈P{\displaystyle u\in P} называется верхней гранью, если ∀x∈Sx⩽u{\displaystyle \forall x\in S\;x\leqslant u}.
Допустим, что любое линейно упорядоченное подмножество множества P{\displaystyle P} имеет верхнюю грань. Тогда ∃m∈P∄x∈Px>m{\displaystyle \exists m\in P\;\nexists x\in P\;x>m}, то есть m{\displaystyle m} — максимальный элемент.

Принцип максимума Хаусдорфа[править | править код]

Если ограничить применение аксиомы выбора только конечными и счётными семействами множеств, получается «аксиома счётного выбора». Она вполне достаточна для обоснования большинства теорем анализа и не создаёт указанных выше парадоксов. Однако её недостаточно для обоснования многих положений теории множеств. Ещё один, несколько более сильный вариант — Аксиома зависимого выбора^[en], но и она не подходит для нужд теории множеств.

В 1962 году польские математики Ян Мычельский и Гуго Штейнгауз предложили взамен аксиомы выбора так называемую «аксиому детерминированности»^[10]. В отличие от аксиомы выбора, которая имеет интуитивно понятную формулировку и противоречащие интуиции следствия, аксиома детерминированности, наоборот, имеет неочевидную формулировку, однако её следствия куда лучше согласуются с интуицией. Из аксиомы детерминированности вытекает аксиома счётного выбора, но не полная аксиома выбора^[8].

Следствия аксиомы детерминированности в ряде ситуаций противоречат следствиям аксиомы выбора — например, из аксиомы детерминированности следует, что все множества вещественных чисел измеримы по Лебегу, в то время как из аксиомы выбора следует существование неизмеримого по Лебегу множества вещественных чисел. Используя аксиому детерминированности, можно строго доказать, что между счётной мощностью и мощностью континуума нет промежуточных мощностей, в то время как это утверждение независимо от аксиомы выбора^[11].

↑ семейство в математике — множество множеств.
↑ ¹ ² Выбора аксиома // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1.
↑ ¹ ² Куратовский К., Мостовский А. Теория множеств / Перевод с английского М. И. Кратко под редакцией А. Д. Тайманова. — М.: Мир, 1970. — С. 61. — 416 с.
↑ ¹ ² John L. Bell. The Axiom of Choice (неопр.). Stanford Encyclopedia of Philosophy. Дата обращения 17 марта 2020.
↑ Элементы: Пределы доказуемости
↑ Виленкин Н. Я. Рассказы о множествах. — 3-е изд. — М.: МЦНМО, 2005. — С. 95. — 150 с. — ISBN 5-94057-036-4.
↑ П. Дж. Коэн. Теория множеств и континуум-гипотеза. — Москва: Мир, 1969.
↑ ¹ ² Казимиров Н. И. Введение в аксиоматическую теорию множеств. Учебное пособие. — Петрозаводск, 2000. — 104 с. — § 2.4.
↑ Евгений Вечтомов. Математика: основные математические структуры 2-е изд. Учебное пособие для академического бакалавриата. — Litres, 2018. — С. 26. — 297 с.
↑ Mycielski, Jan; Steinhaus, H. (1962). A mathematical axiom contradicting the axiom of choice. Bulletin de l'Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques 10: 1–3. ISSN 0001-4117. MR 0140430.
↑ Кановей В. Г., 1984, с. 4, 37.

Выбор из противположностей Пабло Эскобара: аксиома или требует доказательств?

Вы слышали высказывание Пабло Эскобара, которое часто называют "аксиома Эскобара"? Не столь важно, кто он таков, но его слова очень четко отображают проблему выбора между двумя неугодными нам альтернативами.

Кто такой Пабло Эскобар?

Чаще всего теоремы или аксиомы принадлежат уму и деятельности математиков или физиков, между тем дело с теоремой Эскобара обстоит несколько иначе. Пабло Эмилио Эскобар - это наркобарон из Колумбии, который был застрелен в 1993 году. При жизни он в силу своей профессии изъяснялся в основном нецензурно и не делал открытий в математике или физике. Между тем его авторству принадлежит достаточно известная фраза, которая иллюстрирует безальтернативный выбор. В переводе на русский и в цензурном виде она звучит так: "Если вы выбираете из двух противоположностей в безальтернативной ситуации, оба варианта будут представлять собой ерунду". Данная аксиома стала известной достаточно случайно, после публикации на портале "Луркмор". Сейчас данный ресурс зарыт, но "теорема" разлетелась по Сети и стала достаточно известной.

Это теорема или аксиома? Теорема нуждается в подтверждении, в то время как аксиома - это постулат, истина, не требующая доказательств. Высказывание Пабло Эскобара на самом деле не нуждается в аргументах "за", поэтому правильнее называть его "аксиомой".

Синонимы к высказыванию Эскобара

Аксиома наркобарона не первая в истории достаточно четко отображает ситуацию, когда перед нами как выбор встают два неудобных варианта. Вспомните поговорку "из двух зол выбирают меньшее", смысл который близок к словам Эскобара. Аксиома в данном случае такова: если оба варианта вам не по душе, а альтернативы нет, просчитайте, при выборе какого вы потеряете меньше.

Между Сциллой и Харибдой

Еще одно синонимичное высказывание относится к крылатым выражениям греческой мифологии и звучит как "между Сциллой и Харибдой". Когда Одиссей находился в плавании, ему пришлось на корабле проходить опасное место, расположенное между двумя скалами. В одной скале, под названием Харибда, была пещера, обитель страшного монстра. А на горе Сцилле жила злая морская богиня. Миновать скалы, просто обойти их было нельзя, и потому Одиссей решил проплыть мимо Сциллы. Как просчитал Одиссей, чудовище погубило бы максимум половину команды, в то время как морская богиня убила бы всю команду и самого Одиссея. Так и поступив, знаменитый мореплаватель спас большую часть команды.

Также в русском языке есть высказывания "из огня да в полымя", "между молотом и наковальней", которые значат все то же самое - в случае двух безальтернативных возможностей все равно придется что-то выбирать, но нас этот выбор не обрадует.

Выбор в современных реалиях

Как теорема Эскобара выглядит в реальной жизни? Мы постоянно сталкиваемся с ситуациями, когда нужно выбирать между альтернативами совершенно безрадостными. Представьте, что вам нужна ваша работа из-за зарплаты, на которую вы содержите вашу семью. В то же время ваш начальник вам говорит, что придется оставаться в течение месяца до поздна, иначе он вас уволит. Вы понимаете, что если вас уволят, то найти подходящую работу будет очень непросто. И что выбрать? Вы работаете ради своих близких, но вам придется отказаться на время от них, чтобы добывать средства на жизнь. Если же вы выберете родных, то не факт, что вы в ближайшее время найдете деньги на их содержание. И тот, и другой вариант вам не нравятся, но вы выберете меньшее из зол.

Выбор есть всегда

Теорема Эскобара предполагает наличие всего двух вариантов, каждый из которых нам не нравится. Но между тем реальность предполагает, как правило, куда больше возможностей. Столкнулись с безальтернативной ситуацией? Взгляните на нее под другим углом, может быть, вы не учли всех возможностей. Очень часто мы "зашториваемся" и закрываемся от выбора, который лежит в иной плоскости. Чтобы не стать жертвой теоремы Пабло Эскобара, аксиома следующая - позвольте себе посмотреть на проблему другими глазами. Дайте себе время, станьте безучастным равнодушным наблюдателем, попросите совета у близких или родных. Наряду с "двумя злами" есть и другое высказывание - "выбор есть всегда". И поверьте, что дело кроется не только в "Сцилле и Харибде", есть возможность повернуть назад или избрать совершенно иной путь. Господина Эскобара аксиома - спорное утверждение. Очень редко жизнь нам предоставляет всего два варианта развития событий.

Аксиома Эскобара — Абсурдопедия

Каждый дождевой червяк выбирает для себя сам: либо мокнуть под дождём на оживлённом тротуаре, либо прятаться возле пруда с лягушками.

~ Чарльз Дарвин про действие аксиомы Эскобара на дождевых червей во время дождя.

Жизнерадостная и гламурная вывеска бара «Эско» — всегда красится либо в чёрный либо в белый цвет

Аксиома Эскобара — частный случай теории множеств, могущий быть описанный следующей фразой:

При безальтернативном выборе из двух противоположных сущностей обе будут являть собой исключительную хрень.

Изначальный вариант аксиомы.

История фразы восходит к завсегдатаям университетского бара «Эско» Эдинбурга, в котором на выбор подавали всего два алкогольных напитка — разбавленное водой пиво и очищенный технический спирт. При отсутствии возможности заказать что либо другое. Например, при попытке заказать красное вино или глинтвейн, математики получали неизменный отказ. Ситуация получила переложение на строгий научный язык. Впоследствии оказалось, что это не просто эмпирическое наблюдение, но настоящая аксиома, успешно подходящая для описания жизненных ситуаций в условиях геометрической несвободы индивидуума.

Пабло Эскобара выгоняют из пивбара по приказу неженатой продавщицы пива сисястой барменши Натальи так как поставки кокаина мешают продажам пива и копанию в трусах

Начинать надо с сотворения мира Великим Апчхибудьздравием, когда выбор состоял из двух возможностей — либо ничего не будет, либо будет Большой Взрыв со столкновениями галактик, взрывами сверхновых звёзд, падением астероидов, борьбой за существование, геноцидом, суицидом и восстанием роботов с последующим экстерминатусом биологических форм жизни и тепловой гибелью вселенной. Такая вот нелепая картинка — либо ты пустое место, либо ты место полное страданий с бесславным концом. Конечно, доброхоты, типа вирусов или Гаутамы Будды, попытались избавить от страданий тех, кому эти страдания небезразличны, но в целом аксиома Эскобара оттопталась по этим существам как могла. Хотя, по мнению иных, не всё так плохо, можно просто прийти после изнурительного рабочего дня домой, выпить чайку, принять ароматную ванну с солью под расслабляющую музыку и полюбоваться закатом.

Кстати, о работе. Когда владелец шарашкиной конторы, производящей блестящие штуковины, предлагает вам поработать круглосуточно либо получать зарплату ниже прожиточного минимума независимо от реальной выделки блестящих штуковин, то стоит либо смириться с аксиомой Эскобара, либо отправиться к буржуину из другой шарашкиной конторы, производящей мохнатые фиговины. И этот, новый, буржуин предложит вам то же самое. Таким образом, согласно всё той же вездесущей аксиоме, остаётся либо стать работодателем самому и испортить себе лазурно-чистую совесть, требуя от своих работников безальтернативного выбора, либо уйти в хикки-затвор. Вариант с хэнсином и превращения в девочку-волшебницу опять же подразумевает как минимум то, что вы — девочка. А даже если так, то будете привлекать к себе внимание вредных девочек-колдуний, которые будут вас как минимум дразнить и ходить по пятам, чтобы отбить мальчиков.

Легче всего переносят действие аксиомы Эскобара мазохисты и любители экзотических рептилий, которые, будучи актёрами в дешёвом историческом кино про расхитителей гробниц, и, согласно сюжету, выбирая по требованию очень плохих дикарей между ямой с крокодилами и гнездом с птеродактилями, буквально разрываются от желания потрепать за мордочку крокодильчика и не менее сильного желания погладить птенца птеродактиля на глазах его разозлённой мамаши.