Энтропия что это такое простыми

Энтропия? Это просто! / Habr

Этот пост является вольным переводом ответа, который Mark Eichenlaub дал на вопрос What's an intuitive way to understand entropy?, заданный на сайте Quora

Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.

Если в двух словах, то

Энтропия — это то, как много информации вам не известно о системе

Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна. Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации.

Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём).

Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).

А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.

Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.

Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:

S = log Ω

Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B.

Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть опеделённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.

Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.

Классической системой, которую рассматривают в физике, является газ, находящийся в сосуде под поршнем. Микросостояние газа — это положение и импульс (скорость) каждой его молекулы. Это эквивалентно тому, что вы знаете значение, выпавшее на каждой кости в рассмотренном раньше примере. Макросостояние газа описывается такими величинами как давление, плотность, объём, химический состав. Это как сумма значений, выпавших на костях.

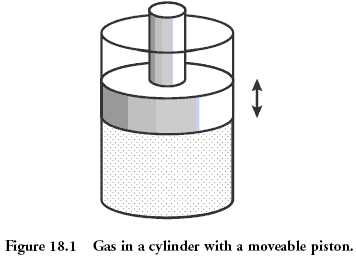
Величины, описывающие макросостояние, могут быть связаны друг с другом через так называемое «уравнение состояния». Именно наличие этой связи позволяет, не зная микросостояний, предсказывать, что будет с нашей системой, если начать её нагревать или перемещать поршень. Для идеального газа уравнение состояния имеет простой вид:

p = ρT

хотя вы, скорее всего, лучше знакомы с уравнением Клапейрона — Менделеева pV = νRT — это то же самое уравнение, только с добавлением пары констант, чтобы вас запутать. Чем больше микросостояний отвечают данному макросостоянию, то есть чем больше частиц входят в состав нашей системы, тем лучше уравнение состояния её описывают. Для газа характерные значения числа частиц равны числу Авогадро, то есть составляют порядка 10²³.

Величины типа давления, температуры и плотности называются усреднёнными, поскольку являются усреднённым проявлением постоянно сменяющих друг друга микросостояний, отвечающих данному макросостоянию (или, вернее, близким к нему макросостояниям). Чтобы узнать в каком микросостоянии находится система, нам надо очень много информации — мы должны знать положение и скорость каждой частицы. Количество этой информации и называется энтропией.

Как меняется энтропия с изменением макросостояния? Это легко понять. Например, если мы немного нагреем газ, то скорость его частиц возрастёт, следовательно, возрастёт и степень нашего незнания об этой скорости, то есть энтропия вырастет. Или, если мы увеличим объём газа, отведя поршень, увеличится степень нашего незнания положения частиц, и энтропия также вырастет.

Если мы рассмотрим вместо газа какое-нибудь твёрдое тело, особенно с упорядоченной структурой, как в кристаллах, например, кусок металла, то его энтропия будет невелика. Почему? Потому что зная положение одного атома в такой структуре, вы знаете и положение всех остальных (они же выстроены в правильную кристаллическую структуру), скорости же атомов невелики, потому что они не могут улететь далеко от своего положения и лишь немного колеблются вокруг положения равновесия.

Если кусок металла находится в поле тяготения (например, поднят над поверхностью Земли), то потенциальная энергия каждого атома в металле приблизительно равна потенциальной энергии других атомов, и связанная с этой энергией энтропия низка. Это отличает потенциальную энергию от кинетической, которая для теплового движения может сильно меняться от атома к атому.

Если кусок металла, поднятый на некоторую высоту, отпустить, то его потенциальная энергия будет переходить в кинетическую энергию, но энтропия возрастать практически не будет, потому что все атомы будут двигаться приблизительно одинаково. Но когда кусок упадёт на землю, во время удара атомы металла получат случайное направление движения, и энтропия резко увеличится. Кинетическая энергия направленного движения перейдёт в кинетическую энергию теплового движения. Перед ударом мы приблизительно знали, как движется каждый атом, теперь мы эту информацию потеряли.

Второй закон термодинамики утверждает, что энтропия (замкнутой системы) никогда не уменьшается. Мы теперь можем понять, почему: потому что невозможно внезапно получить больше информации о микросостояниях. Как только вы потеряли некую информацию о микросостоянии (как во время удара куска металла об землю), вы не можете вернуть её назад.

Давайте вернёмся обратно к игральным костям. Вспомним, что макросостояние с суммой 59 имеет очень низкую энтропию, но и получить его не так-то просто. Если бросать кости раз за разом, то будут выпадать те суммы (макросостояния), которым отвечает большее количество микросостояний, то есть будут реализовываться макросостояния с большой энтропией. Самой большой энтропией обладает сумма 35, и именно она и будет выпадать чаще других. Именно об этом и говорит второй закон термодинамики. Любое случайное (неконтролируемое) взаимодействие приводит к росту энтропии, по крайней мере до тех пор, пока она не достигнет своего максимума.
И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.

Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).

Ну и напоследок рассмотрим решение в рамках нашей парадигмы знаменитого парадокса демона Максвелла. Напомню, что он заключается в следующем. Пусть у нас есть перемешанные газы из синих и красных молекул. Поставим обратно перегородку, проделав в ней небольшое отверстие, в которое посадим воображаемого демона. Его задача — пропускать слева направо только красных, и справа налево только синих. Очевидно, что через некоторое время газы снова будут разделены: все синие молекулы окажутся слева от перегородки, а все красные — справа.

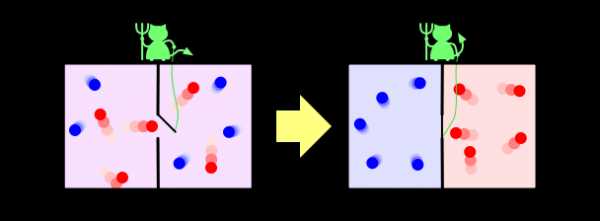
Получается, что наш демон понизил энтропию системы. С демоном ничего не случилось, то есть его энтропия не изменилась, а система у нас была закрытой. Получается, что мы нашли пример, когда второй закон термодинамики не выполняется! Как такое оказалось возможно?

Решается этот парадокс, однако, очень просто. Ведь энтропия — это свойство не системы, а нашего знания об этой системе. Мы с вами знаем о системе мало, поэтому нам и кажется, что её энтропия уменьшается. Но наш демон знает о системе очень много — чтобы разделять молекулы, он должен знать положение и скорость каждой из них (по крайней мере на подлёте к нему). Если он знает о молекулах всё, то с его точки зрения энтропия системы, фактически, равна нулю — у него просто нет недостающей информации о ней. В этом случае энтропия системы как была равна нулю, так и осталась равной нулю, и второй закон термодинамики нигде не нарушился.

Но даже если демон не знает всей информации о микросостоянии системы, ему, как минимум, надо знать цвет подлетающей к нему молекулы, чтобы понять, пропускать её или нет. И если общее число молекул равно N, то демон должен обладать N бит информации о системе — но именно столько информации мы и потеряли, когда открыли перегородку. То есть количество потерянной информации в точности равно количеству информации, которую необходимо получить о системе, чтобы вернуть её в исходное состояние — и это звучит вполне логично, и опять же не противоречит второму закону термодинамики.

Энтропия - что это такое: объяснение простыми словами, значение термина в разных областях науки, примеры

Что такое энтропия? Этим словом можно охарактеризовать и объяснить почти все процессы в жизни человека (физические и химические процессы, а также социальные явления). Но не все люди понимают значение этого термина и уж тем более не все могут объяснить, что это слово значит. Теория сложна для восприятия, но если добавить в неё простые и понятные примеры из жизни, то разобраться с определением этого многогранного термина будет легче. Но обо всём по порядку.

Энтропия: определение и история появления термина

История появления термина

Энтропия как определение состояния системы была введена в 1865 году немецким физиком Рудольфом Клаузиусом, чтобы описать способность теплоты превращаться в другие формы энергии, главным образом в механическую. С помощью этого понятия в термодинамике описывают состояние термодинамических систем. Приращение этой величины связано с поступлением тепла в систему и с температурой, при которой это поступление происходит.

Определение термина из Википедии

Этот термин долгое время использовался только в механической теории тепла (термодинамике), для которой оно вводилось. Но со временем это определение перешло в другие области и теории. Существует несколько определений термина «энтропия».

Википедия даёт краткое определение для нескольких областей, в которых этот термин используется:«Энтропия (от др.-греч. ἐντροπία «поворот»,«превращение») — часто употребляемый в естественных и точных науках термин. В статистической физике характеризует вероятность осуществления какого-либо макроскопического состояния. Помимо физики, этот термин широко используется в математике: теории информации и математической статистике».

Виды энтропий

Этот термин используется в термодинамике, экономике, теории информации и даже в социологии. Что же он определяет в этих областях?

В физической химии (термодинамике)

Основной постулат термодинамики о равновесии: любая изолированная термодинамическая система приходит в равновесное состояние с течением времени и не может из него выйти самопроизвольно. То есть каждая система стремится в равновесное для неё состояние. И если говорить совсем простыми словами, то такое состояние характеризуется беспорядком.

Энтропия — это мера беспорядка. Как определить беспорядок? Один из способов — приписать каждому состоянию число вариантов, которыми это состояние можно реализовать. И чем больше таких способов реализации, тем больше значение энтропии. Чем больше организованно вещество (его структура), тем ниже его неопределённость (хаотичность).

Абсолютное значение энтропии (S абс.) равно изменению имеющейся у вещества или системы энергии во время теплопередачи при данной температуре. Его математическая величина определяется из значения теплопередачи (Q), разделённого на абсолютную температуру (T), при которой происходит процесс: S абс. = Q / T. Это означает, что при передаче большого количества теплоты показатель S абс. увеличится. Тот же эффект будет наблюдаться при теплопередаче в условиях низких температур.

В экономике

В экономике используется такое понятие, как коэффициент энтропии. С помощью этого коэффициента исследуют изменение концентрации рынка и её уровень. Чем выше значение коэффициента, тем выше экономическая неопределённость и, следовательно, вероятность появления монополии снижается. Коэффициент помогает косвенно оценить выгоды, приобретённые фирмой в результате возможной монопольной деятельности или при изменении концентрации рынка.

В статистической физике или теории информации

Информационная энтропия (неопределённость)— это мера непредсказуемости или неопределённости некоторой системы. Эта величина помогает определить степень беспорядочности проводимого эксперимента или события. Чем больше количество состояний, в которых может находиться система, тем больше значение неопределённости. Все процессы упорядочивания системы приводят к появлению информации и снижению информационной неопределённости.

С помощью информационной непредсказуемости можно выявить такую пропускную способность канала, которая обеспечит надёжную передачу информации (в системе закодированных символов). А также можно частично предсказывать ход опыта или события, деля их на составные части и высчитывая значение неопределённости для каждой из них. Такой метод статистической физики помогает выявить вероятность события. С его помощью можно расшифровать закодированный текст, анализируя вероятность появления символов и их показатель энтропии.

Существует такое понятие, как абсолютная энтропия языка. Эта величина выражает максимальное количество информации, которое можно передать в единице этого языка. За единицу в этом случае принимают символ алфавита языка (бит).

В социологии

Здесь энтропия (информационная неопределённость) является характеристикой отклонения социума (системы) или его звеньев от принятого (эталонного) состояния, а проявляется это в снижении эффективности развития и функционирования системы, ухудшении самоорганизации. Простой пример: сотрудники фирмы так сильно загружены работой (выполнением большого количества отчётов), что не успевают заниматься своей основной деятельностью (выполнением проверок). В этом примере мерой нецелесообразного использования руководством рабочих ресурсов будет являться информационная неопределённость.

Энтропия: тезисно и на примерах

Чем больше способов реализации, тем больше информационная неопределённость.

Пример 1. Программа Т9. Если в слове будет небольшое количество опечаток, то программа легко распознает слово и предложит его замену. Чем больше опечаток, тем меньше информации о вводимом слове будет у программы. Следовательно, увеличение беспорядка приведёт к увеличению информационной неопределённости и наоборот, чем больше информации, тем меньше неопределённость.

Пример 2. Игральные кости. Выкинуть комбинацию 12 или 2 можно только одним способом: 1 плюс 1 или 6 плюс 6. А максимальным числом способов реализуется число 7 (имеет 6 возможных комбинаций). Непредсказуемость реализации числа семь самая большая в этом случае.

В общем смысле энтропию (S) можно понимать как меру распределения энергии. При низком значении S энергия сконцентрирована, а при высоком — распределена хаотично.

Пример. Н2О (всем известная вода) в своём жидком агрегатном состоянии будет обладать большей энтропией, чем в твёрдом (лёд). Потому что в кристаллическом твёрдом теле каждый атом занимает определённое положение в кристаллической решётке (порядок), а в жидком состоянии у атомов определённых закреплённых положений нет (беспорядок). То есть тело с более жёсткой упорядоченностью атомов имеет более низкое значение энтропии (S). Белый алмаз без примесей обладает самым низким значением S по сравнению с другими кристаллами.

Связь между информацией и неопределённостью.

Пример 1. Молекула находится в сосуде, который имеет левую и правую часть. Если неизвестно, в какой части сосуда находится молекула, то энтропия (S) будет определяться по формуле S = S max = k * lgW, где k -число способов реализации, W- количество частей сосуда. Информация в этом случае будет равна нулю I = I min =0. Если же точно известно, в какой части сосуда находится молекула, то S = S min =k*ln1=0, а I = I max= log 2 W. Следовательно, чем больше информации, тем ниже значение информационной неопределённости.

Пример 2. Чем выше порядок на рабочем столе, тем больше информации можно узнать о вещах, которые на нём находятся. В этом случае упорядоченность предметов снижает энтропию системы «рабочий стол».

Пример 3. Информация о классе больше на уроке, чем на перемене. Энтропия на уроке ниже, так как ученики сидят упорядочено (больше информации о местоположении каждого ученика). А на перемене расположение учеников меняется хаотично, что повышает их энтропию.

Химические реакции и изменение энтропии.

Пример. При реакции щелочного металла с водой выделяется водород. Водород-это газ. Так как молекулы газа движутся хаотично и имеют высокую энтропию, то рассматриваемая реакция происходит с увеличением её значения. То есть энтропия химической системы станет выше.

В заключение

Если объединить всё вышесказанное, то получится, что энтропия является мерой беспорядка или неопределённости системы и её частей. Интересен тот факт, что всё в природе стремится к максимуму энтропии, а человек — к максимуму информации. И все рассмотренные выше теории направлены на установление баланса между стремлением человека и естественными природными процессами.

Энтропия в классической термодинамике — Википедия

Термодинамическая энтропия S{\displaystyle S}, часто именуемая просто энтропией, — физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин. Энтропия является функцией состояния и широко используется в термодинамике, в том числе технической (анализ работы тепловых машин и холодильных установок) и химической (расчёт равновесий химических реакций).

Утверждение о существовании энтропии и перечисление её свойств составляют содержание второго и третьего начал термодинамики. Значимость данной величины для физики обусловлена тем, что наряду с температурой её используют для описания термических явлений и термических свойств макроскопических объектов. Качественные представления о термическом состоянии системы связаны с тепловыми ощущениями, выражаемыми понятиями «теплее», «холоднее», «нагрев», «охлаждение», «степень нагретости». К термическим относят свойства, характеризующие поведение вещества при его нагреве или охлаждении: термические коэффициенты, теплоёмкость и другие калорические коэффициенты, постоянную Кюри, показатели термостойкости, пределы огнестойкости и т. д.; примерами термических явлений служат термическое расширение, пироэлектричество, электрокалорический эффект, теплопроводность, изменение агрегатного состояния — кристаллизация и замерзание, плавление и таяние, испарение, кипение, сублимация (возгонка), конденсация и другие процессы.

Понятие энтропии, её обозначение и название были введены Р. Клаузиусом (1865). Абстрактность этого понятия — одного из краеугольных камней термодинамики — и разнообразие подходов к обоснованию существования энтропии как термодинамической величины привели к появлению аксиоматики термодинамики.

Термодинамическая дефиниция энтропии[править | править код]

В термодинамике энтропию вводят, обосновывая её существование, перечисляя её свойства и строя для неё шкалу измерения на основании первого, второго и третьего начал термодинамики.

В термодинамических формализмах Клаузиуса^[1] и Каратеодори^[2] энтропию вводят одновременно с абсолютной термодинамической температурой. Математический аппарат термодинамики Гиббса^[3] основан на использовании энтропии в качестве независимой термодинамической переменной, тогда как температура — естественный кандидат на эту роль, вводится как функция внутренней энергии и энтропии. Наконец, в рациональной термодинамике энтропию выражают через внутреннюю энергию и температуру, которые рассматривают как основные неопределяемые переменные теории.

Энтропия простой системы[править | править код]

Первое начало (закон) термодинамики устанавливает связь между внутренней энергией, работой и теплотой: одна из этих физических величин задаётся с помощью двух других, которые, будучи исходными объектами теории, в рамках самой этой теории определены быть не могут просто потому, что не существует понятий более общих, под которые их можно было бы подвести^[4]. Термодинамика заимствует понятия энергии и работы из других разделов физики^[5]^[6], тогда как определение количеству теплоты, наоборот, даётся только и именно в термодинамике. Согласно Клаузиусу теплоту Q{\displaystyle Q} определяют через внутреннюю энергию U{\displaystyle U} и работу W{\displaystyle W}^[7]^[8]. При использовании термодинамического правила знаков^[9] математическое выражение для первого начала термодинамики в формулировке Клаузиуса имеет вид^[10]:

Q≡ΔU−W.{\displaystyle Q\equiv \Delta U-W.}

(Дефиниция теплоты по Клаузиусу)

Первое начало в этой формулировке вводит теплоту как физическую характеристику процесса, поведение которой определяется законом сохранения энергии, но не определяет её как математический объект. Детализировать дефиницию теплоты проще всего для равновесного процесса, когда работу, а следовательно и теплоту, можно выразить через переменные состояния. Для бесконечно малого^[11]равновесного процесса в простой системе^[12] возможен единственный вид работы — работа расширения/сжатия Wv{\displaystyle W_{v}}:

δWv=−PdV,{\displaystyle \delta W_{v}=-PdV,}

(Работа расширения/сжатия для равновесного процесса в простой системе)

где P{\displaystyle P} — давление, V{\displaystyle V} — объём; символ δ{\displaystyle \delta } означает, что соответствующая величина относится к бесконечно малому процессу. Таким образом, для первого начала термодинамики в формулировке Клаузиуса получаем^[13]^[14]:

δQ=dU+PdV,{\displaystyle \delta Q=dU+PdV,}

(Первое начало для равновесного процесса в простой системе)

где δQ{\displaystyle \delta Q} — элементарная (бесконечно малая) теплота процесса.

Это выражение, определяющее элементарную теплоту как математический объект, есть линейная дифференциальная форма (форма Пфаффа) для двух независимых переменных. Для данной пфаффовой формы условие интегрируемости Эйлера не выполняется, то есть δQ{\displaystyle \delta Q} есть функционал^[15], а не полный дифференциал несуществующей функции Q(U,V){\displaystyle Q(U,V)}^[14]. Из теории дифференциальных форм известно, однако, что если выполняется условие Фробениуса^[16], то пфаффова форма имеет интегрирующий множитель/делитель, превращающий эту форму в полный дифференциал и представляющий из себя функцию тех же независимых переменных, которые входят в форму Пфаффа^[17]. Пфаффовы формы, имеющие интегрирующий множитель/делитель называют голономными; пфаффова форма двух переменных всегда голономна (теорема Коши)^[18]^[19]. Поэтому для простых равновесных систем существует функция состояния S(U,V){\displaystyle S(U,V)}, полный дифференциал которой равен

dS ≡ δQT = 1TdU + PTdV,{\displaystyle dS~\equiv ~{\frac {\delta Q}{T}}~=~{\frac {1}{T}}dU~+~{\frac {P}{T}}dV,}

(Дефиниция энтропии простой равновесной системы)

где

T=T(U,V){\displaystyle T=T(U,V)}

есть интегрирующий делитель для формы Пфаффа. Клаузиус назвал функцию состояния S{\displaystyle S} энтропией (от греческого ἐντροπία — изменение, превращение, преобразование). Второе начало термодинамики утверждает, что энтропия существует для любых равновесных систем, а не только простых, и что интегрирующий делитель T{\displaystyle T} есть абсолютная термодинамическая температура^[20]^[21]^[22]^[19]. Неравновесная термодинамика распространяет представление о локальной энтропии и локальной температуре на любые термодинамические системы.

Интегрирование уравнения для энтропии приводит к появлению в выражении для функции S(U,V){\displaystyle S(U,V)} произвольной постоянной, зависящей от выбора начальной точки отсчёта энтропии. Произвол в выборе начального состояния для энтропии устраняет третий закон термодинамики.

Энтропия закрытой системы в термодинамике Клаузиуса — Каратеодори[править | править код]

Традиционный подход к построению термодинамики (аксиоматика Клаузиуса — Каратеодори) основан на использовании представления о внутренней энергии как базовом понятии теории, заимствовании формул для вычисления термодинамической работы из механики и электродинамики сплошных сред, и первом начале термодинамики в формулировке Клаузиуса.

Помимо работы расширения/сжатия система может одновременно выполнять другие виды работ, например работу изменению площади поверхности раздела фаз, работу перемещения в поле тяготения, работу поляризации диэлектрика в электрическом поле и т. д. Объединяет все эти виды работ формальная структурная идентичность расчётных формул друг с другом и с выражением для работы расширения/сжатия^[23]^[24]^[25]:

δWi=Xidxi,{\displaystyle \delta W_{i}=X_{i}dx_{i},}

где δWi{\displaystyle \delta W_{i}} — элементарная работа i{\displaystyle i}-го типа, xi{\displaystyle x_{i}} — обобщённая координата, сопряжённая с обобщённой силой Xi.{\displaystyle X_{i}.} Каждой обобщённой координате соответствует своя обобщённая сила; физические переменные, соответствующие обобщённым координатам и силам, конкретизируют применительно к решаемой задаче^[26]^[27].

Если однородная система одновременно совершает несколько различных видов работ, то они суммируются и полная работа системы δW{\displaystyle \delta W} равна^[23]^[28]^[29]

δW=∑iXidxi,{\displaystyle \delta W=\sum _{i}X_{i}dx_{i},}

(Суммарная работа для равновесного процесса в однородной системе)

а для первого начала термодинамики получаем соотношение^[30]^[31]:

δQ=dU−∑iXidxi,{\displaystyle \delta Q=dU-\sum _{i}X_{i}dx_{i},}

(Первое начало для равновесного процесса в однородной системе)

которое как и в случае простой системы представляет собой форму Пфаффа. Следствием второго начала термодинамики в любой его формулировке является вывод о том, что пфаффова форма δQ{\displaystyle \delta Q} при любом числе переменных всегда голономна^[21] и, следовательно, для любой закрытой термодинамической системы существуют энтропия

S=S(U,{xi}){\displaystyle S=S(U,\{x_{i}\})}

(Энтропия однородной закрытой системы)

и абсолютная термодинамическая температура

T=T(U,{xi}).{\displaystyle T=T(U,\{x_{i}\}).}

Выражение {xi}{\displaystyle \{x_{i}\}} есть сокращение для перечисления x1,x2,...,xi,...{\displaystyle x_{1},x_{2},...,x_{i},...} переменных определённого типа, в данном случае — обобщённых координат.

Энтропия открытой системы[править | править код]

Принимая, что теплота и работа являются двумя единственно возможными формами передачи энергии^[32]^[33]^[34], а изменение энергии, связанное с переносом вещества в открытой системе, есть составная часть общей работы, называемая химической работой (работой перераспределения масс веществ^[35]), в случае однородной открытой системы дифференциальную форму δQ{\displaystyle \delta Q} для закрытой системы следует дополнить слагаемым, учитывающим элементарную химическую работу δZ{\displaystyle \delta Z}^[36]^[37]^[38]^[39]^[40]:

δZ=∑jμjdmj,{\displaystyle \delta Z=\sum _{j}\mu _{j}dm_{j},}

(Химическая работа для равновесного процесса в открытой однородной системе)

где mj{\displaystyle m_{j}} — масса j{\displaystyle j}-го компонента^[41], μj{\displaystyle \mu _{j}} — химический потенциал этого компонента.

Пфаффова форма δQ{\displaystyle \delta Q} для открытой однородной системы равна^[29]

δQ=dU−∑iXidxi−∑jμjdmj.{\displaystyle \delta Q=dU-\sum _{i}X_{i}dx_{i}-\sum _{j}\mu _{j}dm_{j}.}

(Первое начало для равновесного процесса в открытой однородной системе)

Дальнейшие рассуждения о существовании энтропии

S=S(U,{xi},{mj}){\displaystyle S=S(U,\{x_{i}\},\{m_{j}\})}

и абсолютной термодинамической температуры

T=T(U,{xi},{mj}){\displaystyle T=T(U,\{x_{i}\},\{m_{j}\})}

для открытой системы ничем не отличаются от соображений, высказанных при рассмотрении закрытой системы, поэтому ниже перечислены причины, по которым открытые системы потребовали отдельного рассмотрения.

Первая из этих причин состоит в том, что использование в понятийном аппарате термодинамики химической работы как части общей работы делает неэквивалентными представления об адиабатной изоляции как накладывающей запрет на обмен веществом (то есть любая адиабатно изолированная система есть система закрытая или, говоря иначе, масса есть адиабатически заторможенная величина)^[42]^[43]^[44]^[45], и адиабатной изоляции как допускающей обмен энергией только в форме работы^[46]^[47]. Восстановить эквивалентность приведённых выше формулировок об адиабатной изоляции удаётся, если модифицировать дефиницию теплоты по Клаузиусу, добавив к теплоте и работе третью форму передачи энергии — энергию переноса массы Z{\displaystyle Z}^[48]^[49]:

Q≡ΔU−W−Z,{\displaystyle Q\equiv \Delta U-W-Z,}

(Модифицированная дефиниция теплоты для открытой системы)

где δZ{\displaystyle \delta Z} задаётся выражением для химической работы.

Вторая причина отдельного рассмотрения вопроса об энтропии открытых систем заключается в следующем. За исключением химического потенциала все входящие в пфаффову форму δQ{\displaystyle \delta Q} для открытой системы переменные в рамках термодинамического формализма представляют собой неопределяемые величины, заимствуемые из других разделов физики, что подразумевает необязательность их описания в самой термодинамике. Химический потенциал вводится в термодинамике и либо должен быть отнесён к базовым неопределяемым понятиям, для которых возможно только пояснительное описание, либо же от термодинамики требуется точная дефиниция химического потенциала. Как неопределяемую величину химический потенциал можно вводить одновременно с температурой и энтропией (более, того П. А. Жилин^[50] считает такой подход единственно правильным^[51]), но традиционно химический потенциал предпочитают вводить в рассмотрение как вторичную переменную на основе предварительно сформированного представления об энтропии открытой системы. Для этого вслед за У. Гиббсом^[52]^[45] без доказательства принимают утверждение о существовании энтропии открытой системы^[53]^[54]^[55]

S=S(U,{xi},{mj}){\displaystyle S=S(U,\{x_{i}\},\{m_{j}\})}

(Энтропия открытой однородной системы по Гиббсу; фундаментальное уравнение Гиббса в энтропийном выражении)

как функции состояния, при неизменности масс компонентов совпадающей с энтропией однородной закрытой системы. Из фундаментального уравнения Гиббса в дифференциальной форме^[55]

dS=1TdU−1T∑iXidxi−1T∑jμjdmj{\displaystyle dS={\frac {1}{T}}dU-{\frac {1}{T}}\sum _{i}X_{i}dx_{i}-{\frac {1}{T}}\sum _{j}\mu _{j}dm_{j}}

(Дифференциальная форма фундаментального уравнения Гиббса для энтропии)

находим значения частных производных энтропии:

(∂S∂U){xi},{mj}=1T,{\displaystyle \left({\frac {\partial S}{\partial U}}\right)_{\{x_{i}\},\{m_{j}\}}={\frac {1}{T}},}

(∂S∂xr)U,{xi≠r},{mj}=−XrT,{\displaystyle \left({\frac {\partial S}{\partial x_{r}}}\right)_{U,\{x_{i\neq r}\},\{m_{j}\}}=-{\frac {X_{r}}{T}},}

(∂S∂V)xi≠V,{mj}=PT.{\displaystyle \left({\frac {\partial S}{\partial V}}\right)_{x_{i}\neq V,\{m_{j}\}}={\frac {P}{T}}.}

Химический потенциал k{\displaystyle k}-го компонента выразим через частную производную энтропии по массе этого компонента^[56]:

μk≡−T(∂S∂mk)U,{xi},{mj≠k}.{\displaystyle \mu _{k}\equiv -T\left({\frac {\partial S}{\partial m_{k}}}\right)_{U,\{x_{i}\},\{m_{j\neq k}\}}.}

(Дефиниция химического потенциала компонента)

Построение теории на основе постулирования существования энтропии как функции состояния, в состав независимых переменных которой входят массы компонентов, составляет главное содержание термодинамики Гиббса^[57], а способ, каким выполнено распространение термодинамики Клаузиуса на открытые системы, позволяет говорить об аксиоматике Гиббса^[52]^[45]. В термодинамике Гиббса вводят понятия компонента системы, фазы и многофазной гетерогенной системы, постулируют существование внутренней энергии U{\displaystyle U} и энтропии S{\displaystyle S} как аддитивных переменных состояния, постулируют связь этих величин с независимыми переменными состояния в виде фундаментальных уравнений Гиббса в энергетическом и энтропийном выражениях, постулируют аддитивность входящих в эти фундаментальные уравнения независимых переменных, постулируют, что T{\displaystyle T} есть термодинамическая температура, вводят химический потенциал μ{\displaystyle \mu } и постулируют общее условие термодинамического равновесия в системе^[58], рассматриваемое далее в числе свойств энтропии.

Обратите внимание, что содержательную дефиницию температуры по Гиббсу^[59]^[60]^[61]

Что такое Энтропия - Узнай Что Такое

Определение энтропии

Энтропия (от др. греч. entropia — "поворот к" / "трансформация") — это мера хаоса, беспорядка или неопределённости в какой-то системе. Существует теория, что всё в мире идёт от порядка в сторону беспорядка, и энтропия измеряет эти изменения.

Пример энтропии — таяние льда в воде. В это время будет увеличиваться энтропия — это происходит когда идёт изменение от сформированного состояния к свободному, т. е. от упорядоченного к неупорядоченному.

Единица измерения энтропии называется энтропийной единицей — Дж/К, ккал/К.

Формула энтропии

Существует несколько вариантов формулы энтропии. Одна из них:

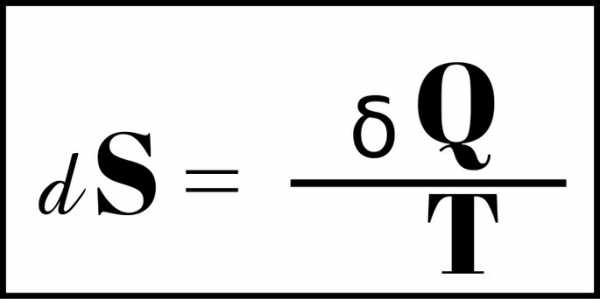"S" — мера энтропии;
"Q" — мера тепла;
"Т" — температура системы (в градусах Кельвина).

Энтропия в физике

Простыми словами энтропия — это мера распределения энергии. Когда энтропия высокая — энергия распределена, когда низкая — энергия сконцентрирована.

Энтропия в термодинамике

Энтропия — это термодинамическое количество, которое показывает сколько энергии в системе, которая уже не доступна для выполнения механической работы.

Энтропия Вселенной

Во втором законе термодинамики говорится, что в спонтанном процессе общая энтропия Вселенной постоянно увеличивается; это означает, что она становится более неупорядоченной, хаотичной.

Энтропия идеального газа

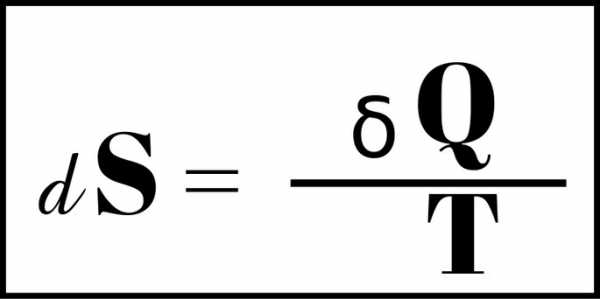
Энтропия системы

Энтропия — это мера случайной активности в системе, мера тепловой энергии системы на единицу температуры, которая недоступна для выполнения полезной работы.

Количество энтропии — это ещё и мера молекулярного беспорядка или случайности системы.

Эту концепцию открыл немецкий физик Рудольф Юлиус Эмануэль Клаузиус в 1850 году.

Энтропия в химии

Энтропия — функция состояния каждого вещества. Энтропия веществ меняется когда происходит химическая реакция. Это изменение энтропии веществ (ΔS) называется "энтропия реакции" или "изменение энтропии в процессе".

Это включает все вещества в реакции, и указывает на состояние системы, а то, как это состояние было достигнуто игнорируется.

Чем выше степень неупорядоченности системы, тем выше энтропия системы.

Разница между энтальпией и энтропией

Простыми словами, энтропия — это мера количества случайности или беспорядка в системе, т. е. мера случайной активности в системе. В то время как энтальпия — это мера общего количества энергии в системе.

Смотрите также, что такое Полимер.

Дата обновления 20/01/2020.

Другие значения и понятия, которые могут вас заинтересовать

Энтропия: что это такое простыми словами

Русский язык, как и любой другой, постоянно изменяется под прессом постоянного технологического заимствования и сотрудничества с другими государствами. Благодаря этому, наш язык богат на различные иноязычные заимствования. Одним из относительно новых слов в русском языке стало слово «энтропия», которое встречалось многим из нас, но далеко не каждый понимает, что же оно на самом деле значит. Данная статья призвана помочь вам разобраться, что же такое энтропия, откуда она «есть-пошла» и в каких сферах жизни используется.

Что такое энтропия простыми словами

Чаще всего слово «энтропия» встречается, конечно же, в классической физике. Это одно из самых сложных понятий данной науки, поэтому даже студенты физических вузов нередко сталкиваются с проблемами при восприятии данного термина. Это, безусловно, физический показатель, однако важно понять один факт – энтропия не похожа на привычные нам понятия объема, массы или давления, потому что энтропия является именно свойством определенной рассматриваемой нами материи.

Говоря простым языком, энтропия – показатель того, насколько много информации об определенном предмете нам неизвестно. Ну, например, на вопрос, где я живу, я отвечу вам – в Москве. Это вполне конкретная координата – столица Российской Федерации – однако, Москва город немаленький, поэтому вам всё еще остается неизвестной точная информация о моем местоположении. А вот когда я назову вам свой, например, почтовый индекс, то энтропия обо мне, как предмете, понизится.

Это не совсем точная аналогия, поэтому для уточнения приведем ещё один пример. Допустим, мы с вами возьмем десять игральных шестигранных кубиков. Бросим их все по очереди, а затем я сообщу вам сумму выпавших показателей – тридцать. Исходя из суммы всех результатов, вы не сможете точно сказать, какая цифра и на каком кубике выпала – вам банально не хватает для этого данных. В нашем случае каждая выпавшая цифра на языке физиков будет называться микросостоянием, а сумма, равная тридцати, на всё том же физическом наречии будет именоваться макросостоянием. Если мы посчитаем, сколько возможных микросостояний могут нам в сумме дать три десятка, то придем к выводу, что их количество достигает почти трёх миллионов значений. Используя специальную формулу, мы можем посчитать и показатель энтропии в данном вероятностном эксперименте – шесть с половиной. Откуда взялась половина, возможно, спросите вы? Эта дробная часть появляется из-за того, что при нумерации в седьмом порядке мы можем оперировать лишь тремя числами – 0, 1 и 2.

Современное слово «энтропия» имеет греческие корни, поэтому из-за перевода её нередко называют «мерой хаоса». Допустим, вы решили устроить у себя в квартире застолье по поводу дня рождения маленькой дочери. Убрали всю квартиру, перемыли полы и окна, вымыли дочиста посуду, а затем красиво и элегантно разложили всю посуду на столе. Изначальный бытовой хаос вашей квартиры значительно уменьшился, следовательно, ваш дом стал системой с маленькой энтропией.

Энтропия во Вселенной

По прогнозам астрофизиков, один из вариантов развития Вселенной – это тепловая смерть. Наша вселенная представляет собой (представьте, насколько прозорливыми были в этом плане древние греки) сущий хаос, в котором постоянно что-нибудь происходит: рождаются и умирают звезды, образуются новые галактики, короче, красота! В один прекрасный момент энтропия Вселенной достигнет максимума и происходить в ней станет попросту нечему. Вот вам и смерть от безделья.

Хаосом пронизан весь космос, вся наша природа, вплоть до атомов и элементарных частиц. Всё находится в постоянном движении и взаимодействии, словно прекрасно сработанный механизм. А управляют всеми этими процессами законы, которые мы, жалкие людишки, можем выразить не менее прекрасным математическим языком. Но как же при таком уровне энтропии (то есть, хаоса) во Вселенной вообще могло что-либо возникнуть?

Ответ на этот вопрос крайне прост. Вся материя передает уровень своей энтропии своему же окружению, всему, до чего могут дотянуться. Например, для регуляции уровня энтропии на Земле – звезда по имени Солнце постоянно снабжает нас энергией, которую производит за счет непрекращающейся термоядерной реакции на ее поверхности. Если бы наша планета была замкнутой системой, то, согласно второму закону термодинамики, энтропия внутри неё могла бы лишь увеличиваться, но, как вы уже поняли, Солнце позволяет нам держать уровень энтропии Земли в норме.

Энтропией и хаосом пропитано всё, что нас окружает и даже то, что находится внутри нас. В газах и жидкостях энтропия играет ключевые роли, даже наши сиюминутные желания и порывы на самом деле являются ничем иным, как порождением всеобщего вселенского хаоса. Не сложно прийти в очередной раз к красивейшему выводу: Вселенная, сколько огромна бы она ни была, представляет собой совокупность бесконечного количества частичек самой разнообразной величины и не менее разнообразных свойств. Всё в ней от элементарного бозона до Альфа Центавры и целых галактик связано незаметными нитями.

Подобные открытия физиков поражают не только своей сложностью, но и красотой. Казалось бы, обычные математические и физические формулы на досках небритых задумчивых мужчин в очках являются ключевыми факторами для нашего познания самих и себя и нашего места в огромной Вселенной. Надеемся, что данная статья помогла вам прояснить, чем же на самом деле является энтропия, в каких случаях данное слово используется, а также к чему открытие данного показателя привело ученых и философов.

Кто знает, быть может прочтение этой статьи вдохновит вас на целенаправленное изучение этой прекрасной науки – физики. Так или иначе, интересоваться наукой современному человеку просто жизненно необходимо, хотя бы для собственного развития.

Как энтропия управляет нашей жизнью

Представьте, что вы взяли коробку с пазлом и высыпали все кусочки мозаики на стол. В теории кусочки могут упасть на свои места так, что картинка сразу сложится целиком. Но в жизни так никогда не бывает. Почему?

Потому что шансы на это ничтожно малы, ведь каждый кусочек пазла должен упасть только одним определённым образом, чтобы картина сложилась. С точки зрения математики, вероятность, что это произойдёт случайно, минимальна.

Что такое энтропия

jamesclear.com

Энтропия — это мера неупорядоченности. И она всегда увеличивается со временем. Всё естественным образом стремится к беспорядку. Здания разрушаются. Машины ржавеют. Люди стареют. Даже горы постепенно рассыпаются.

Это правило, известное как второе начало термодинамики, — один из фундаментальных законов нашей Вселенной. Оно гласит, что в изолированной системе энтропия остаётся неизменной или увеличивается (но никогда не уменьшается).

Но не стоит впадать в панику, есть и хорошие новости. Мы можем сопротивляться силам энтропии. Мы можем собрать рассыпавшийся пазл. Прополоть заросший сад. Убраться в захламлённой комнате. Организовать разрозненных людей в сплочённую команду.

Так как Вселенная стремится к беспорядку, нам приходится затрачивать энергию, чтобы создать в своей жизни стабильность и упорядоченность.

Чтобы отношения были успешными, нужны забота и внимание. Чтобы дом был в хорошем состоянии, его нужно ремонтировать и содержать в чистоте. Для успеха команды необходимы общение и сотрудничество. Если не прилагать усилий, всё будет стремиться к распаду.

Этот вывод — что беспорядок со временем всегда увеличивается, и мы можем противостоять этому, затрачивая энергию, — открывает главную цель жизни. Мы должны прилагать усилия, чтобы создавать порядок, который сможет устоять перед неумолимым напором энтропии.

Как энтропия проявляется в нашей жизни

С помощью энтропии можно объяснить многие непонятные и удивительные факты, например:

Почему наша жизнь так необыкновенна

Представьте человеческий организм. Атомы, из которых состоит тело, могли бы сложиться практически в бесконечное количество вариантов и не создать никакой формы жизни. C точки зрения математики, вероятность нашего существования очень мала. И всё-таки мы существуем.

Во Вселенной, где всем заправляет энтропия, наличие жизни с такой чёткой устойчивой организацией поразительно.

Почему нам нравятся искусство и красота

С помощью энтропии можно объяснить, почему искусство и красота кажутся нам такими эстетически привлекательными. Художник создаёт особую форму порядка и симметрии, какую Вселенная, скорее всего, никогда не породила бы самостоятельно. Число красивых комбинаций гораздо меньше общего количества всех комбинаций. Красота — редкость во Вселенной, полной беспорядка. Поэтому симметричное лицо редко и красиво, ведь несимметричных вариантов несравнимо больше.

Почему идеальные для себя условия нужно не найти, а создать

У каждого из нас свои таланты, навыки и интересы. Но общество и культура, в которых мы живём, не создавались специально под нас. Помня об энтропии, подумайте, каковы шансы, что условия, в которых вы выросли, идеальны для раскрытия ваших талантов?

Крайне маловероятно, что жизнь создаст для вас ситуацию, идеально подходящую под ваши способности. Скорее всего, вы окажетесь в положении, не совсем соответствующем вашим навыкам и потребностям.

Мы обычно описываем такое состояние, как «не в своей тарелке», «не в своей стихии». Естественно, в таких условиях гораздо сложнее добиться успеха, принести пользу, победить. Зная это, мы должны сами создавать для себя идеальные условия жизни.

Сложности в жизни возникают не потому, что планеты так выстроились, и не потому, что какие-то высшие силы сговорились против вас. Это просто действует закон энтропии. Состояний беспорядка гораздо больше, чем упорядоченных. Учитывая всё это, удивительно не то, что в жизни есть проблемы, а то, что мы можем их разрешать.

Энтропия что это такое простыми словами

Простыми словами про энтропию можно сказать так:энтропия-это беспорядок,хаос.Но это очень грубо,просто неграмотно.Поэтому надо всё-таки надо поднапрячься и разобраться посеръёзней.

Обратимся ко второму началу термодинамики.Оно утверждает:

В изолированной системе самопроизвольно могут протекать только такие процессы,которые ведут к увеличению неупорядоченности системы,т.е.к росту энтропии.

И это подтверждает,что энтропия-хаос.Но есть нюансы.Совершенно строго энтропия была введена в термодинамике как функция состояния системы S,изменение которой определяется отношением количества теплоты Q,полученной (или отданной) системой при температуре T, к этой температуре:

S=Q/T

Если изолированная система получает некоторое количество теплоты при постоянной температуре,то вся теплота идёт на увеличение беспорядочного,хаотичного движения частиц,то есть на увеличение энтропии.Так происходит при плавлении вещества или при его испарении,например при кипении(лёд плавится и вода и кипит при постоянной температуре).Наоборот,порядок увеличивается,например при кристаллизации(замерзании) жидкости,энтропия системы уменьшается и выделяется скрытая теплота плавления.

В газе,где частицы движутся независимо,неупорядоченность гораздо больше,чем в кристалле.Жидкость занимает промежуточное положение.Соответственно,и энтропия вещества в газообразном состоянии больше,чем в жидком,а в жидком больше,чем в твердом.

При обсуждении химических проблем удобно пользоваться определением энтропии,данном Больцманом.

Энтропия ( S ) пропорциональна логарифму термодинамической вероятности ( W ) состояния системы: S = k lnW,

где k — постоянная Больцмана,а термодинамическая вероятность W определяется числом микросостояний,которыми может осуществляться рассматриваемое (макро)состояние.

Вот простой пример соотношения макро- и микросостояния системы.Система-кинозал с 10 рядами по 10 кресел и 100 зрителей.Для наилучшего обзора экрана зрители должны быть рассажены строго по росту с первого по 100 место.Это единственное микросостояние.Если рассадить зрителей по росту в только колонках,то число микросостояний будет равно числу сочетаний из 100 по 10,что составляет 10¹³

Но если зрители будут рассаживаться произвольно,число микростояний будет равно 100! и это будет самая неупорядоченная система.

В химии же системы такие,что число частиц очень велико.Например,один моль составляет 6·10²³

частиц и число микросостояний становится невообразимо большим.

Увеличение энтропии означает возможность самопроизвольного протекания таких процессов,как диффузия газов и жидкостей,любой процесс растворения,осмос.

Второе начало термодинамики говорит только о направлении изменения энтропии в процессе,но ничего не говорит об абсолютном значении энтропии.В 19 столетии путем экспериментов были установлены температурные зависимости энтропии для газов и жидкостей при фазовых переходах.При понижении температуры энтропия медленно уменьшается,а при конденсации газа и при кристаллизации жидкости уменьшается резко, скачком.

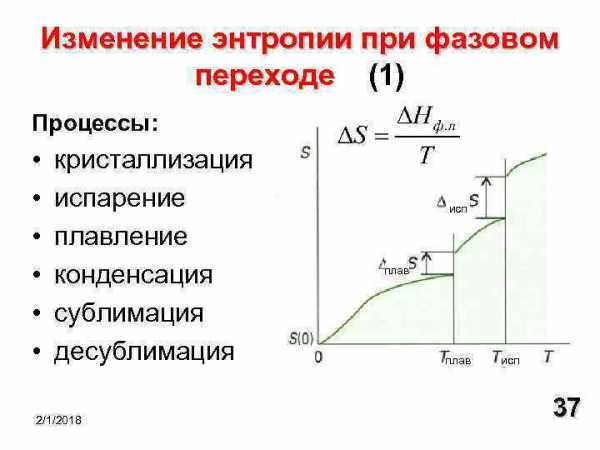
В 1911 году М.Планк постулировал:

Для идеального кристалла при стремлении температуры к абсолютному нулю,энтропия также стремится к нулю.

Третье начало термодинамики гласит:

Энтропия идеального кристалла при 0 K равна нулю.

Таким образом,значения энтропии отсчитываются от нуля и могут быть найдены для любого состояния вещества и любых условий.

Энтропия измеряется в единицах Дж/K и относится к определённому количеству вещества,обычно к 1 моль.Для веществ в одинаковых состояниях энтропия увеличивается с ростом молярной массы.

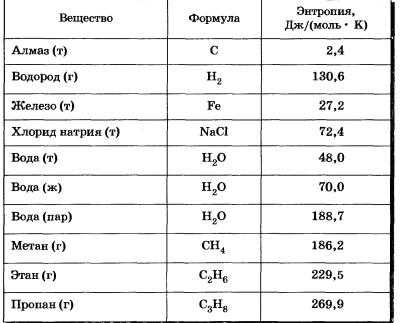Значения энтропии для некоторых веществ при обычной температуре.

Таким образом,появилась ещё одна характеристика химической реакции-изменение энтропии и ещё один критерий-стремление системы к максимуму энтропии.

Итак,ещё раз,энтропия простыми словами-это функция состояния системы (системой может быть простое вещество).

Информационная энтропия — Википедия

Информацио́нная энтропи́я — мера неопределённости некоторой системы (в статистической физике или теории информации), в частности непредсказуемость появления какого-либо символа первичного алфавита. В последнем случае при отсутствии информационных потерь энтропия численно равна количеству информации на символ передаваемого сообщения.

Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределённость появления для некоторых букв меньше, чем для других. Если же учесть, что некоторые сочетания букв (в этом случае говорят об энтропии n{\displaystyle n}-го порядка, см. ниже) встречаются очень редко, то неопределённость уменьшается еще сильнее.

Информационная двоичная энтропия для независимых случайных событий x{\displaystyle x} с n{\displaystyle n} возможными состояниями, распределённых с вероятностями pi{\displaystyle p_{i}} (i=1,...,n{\displaystyle i=1,...,n}), рассчитывается по формуле

H(x)=−∑i=1npilog2⁡pi.{\displaystyle H(x)=-\sum _{i=1}^{n}p_{i}\log _{2}p_{i}.}

Эта величина также называется средней энтропией сообщения. Величина Hi=−log2⁡pi{\displaystyle H_{i}=-\log _{2}{p_{i}}} называется частной энтропией, характеризующей только i{\displaystyle i}-e состояние. В общем случае основание логарифма в определении энтропии может быть любым, большим 1; его выбор определяет единицу измерения энтропии. Так, зачастую (например, в задачах математической статистики) более удобным может оказаться применение натурального логарифма.

Таким образом, энтропия системы x{\displaystyle x} является суммой с противоположным знаком всех относительных частот появления состояния (события) с номером i{\displaystyle i}, умноженных на их же двоичные логарифмы^[1]. Это определение для дискретных случайных событий можно формально расширить для непрерывных распределений, заданных плотностью распределения вероятностей, однако полученный функционал будет обладать несколько иными свойствами (см. дифференциальная энтропия).

Определение по Шеннону[править | править код]

Клод Шеннон предположил, что прирост информации равен утраченной неопределённости, и задал требования к её измерению:

мера должна быть непрерывной; то есть изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение функции;
в случае, когда все варианты (буквы в приведённом примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать значение функции;
должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых значение функции конечного результата должно являться суммой функций промежуточных результатов.^{[прояснить]}

Поэтому функция энтропии H{\displaystyle H} должна удовлетворять условиям

H(p1,…,pn){\displaystyle H(p_{1},\;\ldots ,\;p_{n})} определена и непрерывна для всех p1,…,pn{\displaystyle p_{1},\;\ldots ,\;p_{n}}, где pi∈[0,1]{\displaystyle p_{i}\in [0,\;1]} для всех i=1,…,n{\displaystyle i=1,\;\ldots ,\;n} и p1+…+pn=1{\displaystyle p_{1}+\ldots +p_{n}=1}. (Нетрудно видеть, что эта функция зависит только от распределения вероятностей, но не от алфавита.)
Для целых положительных n{\displaystyle n}, должно выполняться следующее неравенство:
H(1n,…,1n)⏟n<H(1n+1,…,1n+1)⏟n+1.{\displaystyle H\underbrace {\left({\frac {1}{n}},\;\ldots ,\;{\frac {1}{n}}\right)} _{n}<H\underbrace {\left({\frac {1}{n+1}},\;\ldots ,\;{\frac {1}{n+1}}\right)} _{n+1}.}
Для целых положительных bi{\displaystyle b_{i}}, где b1+…+bk=n{\displaystyle b_{1}+\ldots +b_{k}=n}, должно выполняться равенство
H(1n,…,1n)⏟n=H(b1n,…,bkn)+∑i=1kbinH(1bi,…,1bi)⏟bi.{\displaystyle H\underbrace {\left({\frac {1}{n}},\;\ldots ,\;{\frac {1}{n}}\right)} _{n}=H\left({\frac {b_{1}}{n}},\;\ldots ,\;{\frac {b_{k}}{n}}\right)+\sum _{i=1}^{k}{\frac {b_{i}}{n}}H\underbrace {\left({\frac {1}{b_{i}}},\;\ldots ,\;{\frac {1}{b_{i}}}\right)} _{b_{i}}.}

Шеннон показал,^[2] что единственная функция, удовлетворяющая этим требованиям, имеет вид

−K∑i=1np(i)log2⁡p(i),{\displaystyle -K\sum _{i=1}^{n}p(i)\log _{2}p(i),}

где K{\displaystyle K} — положительная константа (и в действительности нужна только для выбора единицы измерения энтропии; изменение этой константы равносильно изменению основания логарифма).

Шеннон определил, что измерение энтропии (H=−p1log2⁡p1−…−pnlog2⁡pn{\displaystyle H=-p_{1}\log _{2}p_{1}-\ldots -p_{n}\log _{2}p_{n}}), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надёжной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислить математическое ожидание «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т. д. (см. цепи Маркова).

Определение энтропии Шеннона связано с понятием термодинамической энтропии. Больцман и Гиббс проделали большую работу по статистической термодинамике, которая способствовала принятию слова «энтропия» в информационную теорию. Существует связь между термодинамической и информационной энтропией. Например, демон Максвелла также противопоставляет термодинамическую энтропию информации, и получение какого-либо количества информации равно потерянной энтропии.

Определение с помощью собственной информации[править | править код]

Также можно определить энтропию случайной величины, введя предварительно понятия распределения случайной величины X{\displaystyle X}, имеющей конечное число значений:^[3]

PX(xi)=pi,pi⩾0,i=1,2,…,n{\displaystyle P_{X}(x_{i})=p_{i},\quad p_{i}\geqslant 0,\;i=1,\;2,\;\ldots ,\;n}

∑i=1npi=1{\displaystyle \sum _{i=1}^{n}p_{i}=1}

и собственной информации:

I(X)=−log⁡PX(X).{\displaystyle I(X)=-\log P_{X}(X).}

Тогда энтропия определяется как:

H(X)=E(I(X))=−∑i=1np(i)log⁡p(i).{\displaystyle H(X)=E(I(X))=-\sum _{i=1}^{n}p(i)\log p(i).}

Единицы измерения информационной энтропии[править | править код]

От основания логарифма зависит единица измерения количества информации и энтропии: бит, нат, трит или хартли.

Энтропия является количеством, определённым в контексте вероятностной модели для источника данных. Например, кидание монеты имеет энтропию:

−2(12log2⁡12)=−log2⁡12=log2⁡2=1{\displaystyle -2\left({\frac {1}{2}}\log _{2}{\frac {1}{2}}\right)=-\log _{2}{\frac {1}{2}}=\log _{2}2=1} бит на одно кидание (при условии его независимости), а количество возможных состояний равно:21=2{\displaystyle 2^{1}=2} возможных состояния (значения) ("орёл" и "решка").

У источника, который генерирует строку, состоящую только из букв «А», энтропия равна нулю: −∑i=1∞log2⁡1=0{\displaystyle -\sum _{i=1}^{\infty }\log _{2}1=0}, а количество возможных состояний равно:20=1{\displaystyle 2^{0}=1} возможное состояние (значение) («А») и от основания логарифма не зависит.
Это тоже информация, которую тоже надо учитывать. Примером запоминающих устройств в которых используются разряды с энтропией равной нулю, но с количеством информации равным 1 возможному состоянию, т.е. не равным нулю, являются разряды данных записанных в ПЗУ, в которых каждый разряд имеет только одно возможное состояние.

Так, например, опытным путём можно установить, что энтропия английского текста равна 1,5 бит на символ, что конечно будет варьироваться для разных текстов. Степень энтропии источника данных означает среднее число битов на элемент данных, требуемых для её зашифровки без потери информации, при оптимальном кодировании.

Некоторые биты данных могут не нести информации. Например, структуры данных часто хранят избыточную информацию, или имеют идентичные секции независимо от информации в структуре данных.
Количество энтропии не всегда выражается целым числом битов.

Математические свойства[править | править код]

Неотрицательность: H(X)⩾0{\displaystyle H(X)\geqslant 0}.
Ограниченность: H(X)=−E(log2⁡pi)=∑i=1npilog2⁡1pi=∑i=1npif(gi)⩽f(∑i=1npigi)=log2⁡n{\displaystyle H(X)=-E(\log _{2}p_{i})=\sum _{i=1}^{n}p_{i}\log _{2}{\frac {1}{p_{i}}}=\sum _{i=1}^{n}p_{i}f(g_{i})\leqslant f\left(\sum _{i=1}^{n}p_{i}g_{i}\right)=\log _{2}n}, что вытекает из неравенства Йенсена для вогнутой функции f(gi)=log2⁡gi{\displaystyle f(g_{i})=\log _{2}g_{i}} и gi=1pi{\displaystyle g_{i}={\frac {1}{p_{i}}}}. Если все n{\displaystyle n} элементов из X{\displaystyle X} равновероятны, H(X)=log2⁡n{\displaystyle H(X)=\log _{2}n}.
Если X,Y{\displaystyle X,\;Y} независимы, то H(X⋅Y)=H(X)+H(Y){\displaystyle H(X\cdot Y)=H(X)+H(Y)}.
Энтропия — выпуклая вверх функция распределения вероятностей элементов.
Если X,Y{\displaystyle X,\;Y} имеют одинаковое распределение вероятностей элементов, то H(X)=H(Y){\displaystyle H(X)=H(Y)}.

Эффективность[править | править код]

Алфавит может иметь вероятностное распределение далекое от равномерного. Если исходный алфавит содержит n{\displaystyle n} символов, тогда его можно сравнить с «оптимизированным алфавитом», вероятностное распределение которого равномерное. Соотношение энтропии исходного и оптимизированного алфавита — это эффективность исходного алфавита, которая может быть выражена в процентах. Эффективность исходного алфавита с n{\displaystyle n} символами может быть также определена как его n{\displaystyle n}-арная энтропия.

Энтропия ограничивает максимально возможное сжатие без потерь (или почти без потерь), которое может быть реализовано при использовании теоретически — типичного набора или, на практике, — кодирования Хаффмана, кодирования Лемпеля — Зива — Велча или арифметического кодирования.

b-арная энтропия[править | править код]

В общем случае b-арная энтропия (где b равно 2, 3, …) источника S=(S,P){\displaystyle {\mathcal {S}}=(S,\;P)} с исходным алфавитом S={a1,…,an}{\displaystyle S=\{a_{1},\;\ldots ,\;a_{n}\}} и дискретным распределением вероятности P={p1,…,pn},{\displaystyle P=\{p_{1},\;\ldots ,\;p_{n}\},} где pi{\displaystyle p_{i}} является вероятностью ai{\displaystyle a_{i}} (pi=p(ai){\displaystyle p_{i}=p(a_{i})}), определяется формулой:

Hb(S)=−∑i=1npilogb⁡pi.{\displaystyle H_{b}({\mathcal {S}})=-\sum _{i=1}^{n}p_{i}\log _{b}p_{i}.}

В частности, при b=2{\displaystyle b=2}, мы получаем обычную двоичную энтропию, измеряемую в битах. При b=3{\displaystyle b=3}, мы получаем тринарную энтропию, измеряемую в тритах (один трит имеет источник информации с тремя равновероятными состояниями). При b=e{\displaystyle b=e}, мы получаем информацию измеряемую в натах.

Условная энтропия[править | править код]

Если следование символов алфавита не независимо (например, во французском языке после буквы «q» почти всегда следует «u», а после слова «передовик» в советских газетах обычно следовало слово «производства» или «труда»), количество информации, которую несёт последовательность таких символов (а, следовательно, и энтропия), очевидно, меньше. Для учёта таких фактов используется условная энтропия.

Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (то есть, вероятности двухбуквенных сочетаний):

h2(S)=−∑ipi∑jpi(j)log2⁡pi(j),{\displaystyle H_{1}({\mathcal {S}})=-\sum _{i}p_{i}\sum _{j}p_{i}(j)\log _{2}p_{i}(j),}

где i{\displaystyle i} — это состояние, зависящее от предшествующего символа, и pi(j){\displaystyle p_{i}(j)} — это вероятность j{\displaystyle j} при условии, что i{\displaystyle i} был предыдущим символом.

Например, для русского языка без буквы «ё» H0=5,h2=4,358,h3=3,52,h4=3,01{\displaystyle H_{0}=5,\;H_{1}=4{,}358,\;H_{2}=3{,}52,\;H_{3}=3{,}01}^[4].

Через частную и общую условные энтропии полностью описываются информационные потери при передаче данных в канале с помехами. Для этого применяются так называемые канальные матрицы. Для описания потерь со стороны источника (то есть известен посланный сигнал) рассматривают условную вероятность p(bj∣ai){\displaystyle p(b_{j}\mid a_{i})} получения приёмником символа bj{\displaystyle b_{j}} при условии, что был отправлен символ ai{\displaystyle a_{i}}. При этом канальная матрица имеет следующий вид:

	b1{\displaystyle b_{1}}	b2{\displaystyle b_{2}}	…	bj{\displaystyle b_{j}}	…	bm{\displaystyle b_{m}}

что это такое простыми словами

Что называют «энтропией» на простом языке?

«Entropia«, в переводе с греческого поворот, превращение. Это слово можно определить, как меру беспорядка, стремление к хаосу. Для точного определения энтропии используются математические расчеты. Лучше всего ее эффект показывают примеры термодинамики, в которых процесс перехода тепла в механическую работу не является абсолютным. Часть его будет преобразована в другие виды энергии.

Совсем простой пример энтропии

Представим подготовку квартиры или офиса к праздничному мероприятию. Все вымыто, аккуратно разложено, столы накрыты, стулья расставлены. Получилась маленькая энтропия. Праздник идет по полной программе. Танцы, хлопушки, фейерверки! Гости расходятся. В квартире полный хаос. Вы получаете систему с большим показателем энтропии. Надо приводить помещение в порядок. Вы тратите на уборку свои силы, энергию. Через время величина энтропии в системе снижается. Порядок восстановлен. И все в соответствии со вторым законом термодинамики. Была добавлена энергия извне. И система теперь не может считаться изолированной.

Рудольф Клаузиус и Людвиг Больцман об энтропии

Термин entropia, впервые введенный немецким ученым Рудольфом Клаузисом в 1865-ом г., применялся для объяснения невозможности передачи теплоты из холодного в более теплое тело. Смысл термина определял «уход в себя” или “вовнутрь”. Идея “ухода в себя” в свою очередь заинтересовала учёного из Австрии Людвига Больцмана. Он провел ряд исследовательских работ и дал следующее разъяснение процесса энтропии.

Возьмем за основу любую систему. Например, газ в сосуде. Он имеет ряд характеристик, которые показывают его макросостояние:

температура;
давление;
объем.

Все эти показатели будут неразрывно связаны с микросостоянием системы:

расположение частиц;
скорость движения частиц.

Состояние системы непрерывно меняется. Это стремление к неорганизованности, к увеличению энтропии. И, одновременно, происходит поиск системой своего самого возможного состояния — равновесия. Следовательно, когда мы говорим о росте энтропии, это означает, что эта система пытается прийти к равновесию.

Вне зависимости от того, насколько хаотично будет происходить движение частиц в сосуде, скорость их движения всегда будет приближена к средней величине. В этом случае, энтропия будет максимальной.

Таким образом, считает Больцман, значение энтропии определяет вероятность микросостояния тела.

Энтропия и «демон Максвелла”

Классический пример “демона” рассматривался неоднократно в различных научных работах и трудах. Есть простое и ясное описание его сути данное «отцом кибернетики” Нобертом Винером. Рассмотрим резервуар, наполненный газом. Температура внутри его будет одинаковая. Скорость движения некоторого числа молекул газа больше, чем остальных.

Добавим в конструкцию тепловой двигатель и две трубы. Соединим резервуар и тепловой двигатель трубой. Вторая труба соединит выходное отверстие двигателя и газовую камеру. Входы из резервуара в двигатель и из двигателя в камеру снабдим маленькими дверцами, возле которых будут сидеть маленькие «демоны”. Их задача открыть или закрыть дверцу в зависимости от того как будут двигаться молекулы.

Первый демон будет открывать дверь только молекулам, имеющим большую скорость. Второй пропустит только самые медленные частицы. Итог работы — температура в резервуаре возле первого демона повысится, возле второго — понизится. Получаем источник абсолютно полезной энергии из случайного движения.

Связь между энтропией и информацией

“Демоны” смогли понизить уровень энтропии. Хотя по законам физики, она должна возрастать. С этим парадоксом справился уже венгерский физик Л. Сциллард. Его работа завершила исследование Максвелла.
Во время своей работы демон использует дополнительные силы, которые он тратит на усилия открыть или закрыть дверь. Демон снижает энтропию, но рассчитывается за процесс информации — можно ли пропустить данную частицу, своей энергией.
Мы получаем доказательство, что информация и энтропия неразрывно связаны между собой. Соответственно информация имеет обратную зависимость от энтропии. С помощью информации мы определяем направление движения частиц, определяем их скорость, производим оценку их движения. Под это правило подойдет любая другая категория. Например: разный смысл букв или символов.

На основании этих выводов, К Шеннон стал создателем формулы энтропии, применяемой для учета информации, где первая является мерой хаоса, вторая же несет в себе упорядоченность.

Понятие «энтропии» в настоящее время применяется в математике, информатике, биологии, химии, физике, психоанализе и социологии. Его применяют в случаях, когда надо проследить способность системы к потерям внутренней энергии и распаду, описать направление процесса.

Энтропия – что это такое простыми словами в химии, физике и каков ее коэффициент

Понятие энтропии используется в различных науках: физике, химии, математике, биологии, социологии. Само слово произошло от греческого и обозначает «превращение, изменение». Что это такое простыми словами? Можно сказать, что это мера беспорядка, хаотичности в любой системе. Чем меньше порядка, тем больше ее значение. Если книги стоят на полке, неупорядоченность у них меньше, чем если они лежат кучей.

Что означает термин

Определение данного термина зависит от сферы его применения. В общих словах можно сказать, что это мера беспорядка и необратимого рассеяния энергии. Чем более упорядочена какая-то система, тем энергия более сконцентрирована. Например, если мы поместим горячий предмет в холодную воду, постепенно он остынет, а вода нагреется. Во втором случае энтропия больше.

Важно! Энтропия характеризует беспорядок. Чем она больше, тем меньше система упорядочена.

В качестве системы может выступать что угодно. В физике или химии это обычно газ, жидкость, твердое тело, набор определенного числа частиц. В информатике это может быть текст, в социологии группа людей.

Термин энтропия

В физике

Этот термин используется в таких разделах физики, как термодинамика и статистическая физика. Термодинамика изучает способы передачи и превращения энергии. Она имеет дело с процессами, в которых можно использовать понятие температуры. Именно в термодинамике впервые начали использовать это понятие. Ввел его немецкий ученый Рудольф Клаузиус. Статистическая механика изучает поведение систем из конечного количества частиц, используя для этого методы теории вероятности.

В разных разделах физики этот термин означает несколько разные вещи. В термодинамике это характеристика необратимого рассеяния энергии. В статистической физике эта величина показывает вероятность какого-то состояния.

Это интересно! В чем заключается принцип теории Гюйгенса Френеля

В термодинамике

Энтропия — единственная величина, показывающая направление физических процессов. Что это значит?

В изолированной системе, то есть той, которая не обменивается ни веществом, ни энергией с окружающими предметами, процессы всегда идут так, что неупорядоченность увеличивается. Достигнув максимума, она остается постоянной. В этом суть второго начала термодинамики.
Обратимые процессы не меняют неупорядоченность.
Необратимые процессы всегда идут так, что беспорядок увеличивается.
В открытой системе эта величина может возрастать или оставаться постоянной, возможны и такие процессы, при которых беспорядок уменьшается. То есть вмешательством извне мы можем уменьшить неупорядоченность.

Всякая система, находящаяся в неизменных внешних условиях, со временем приходит в состояние равновесия и не может самостоятельно из него выйти. При этом все ее части будут иметь одинаковую температуру. Это нулевое начало термодинамики.

В равновесии беспорядок больше всего. Например, есть сосуд, разделенный перегородкой. С одной стороны находится один газ, с другой — другой. Если убрать перегородку, постепенно газы смешаются и самостоятельно уже не разделятся снова. Такое состояние будет более беспорядочным, чем состояние, когда газы были разделены.

В физике эта величина — функция состояния системы. Это значит, что она зависит от параметров системы:

температуры,
давления,
объема,
внутренней энергии.

Это интересно! Формула закона полного отражения и преломления света

В статистической механике

В статистической механике это понятие связано с вероятностью получить определенное состояние. Например, для нескольких предметов или частиц она зависит от числа способов их расположить.

Есть несколько определений этой величины. Наиболее простое определение Больцамана. Она равна логарифму вероятности состояния, умноженному на постоянную Больцмана: S=k*ln(W).

Полезное видео: что такое энтропия

Абсолютное значение

Энтропия — величина неотрицательная (больше или равна нулю). Чем ближе температура к абсолютному нулю, тем она тоже ближе к нулю. Это третье начало термодинамики. В первоначальном виде его сформулировал Макс Планк в 1911 году.

Также третье начало термодинамики называют принципом недостижимости абсолютного нуля. Это значит, что при любых процессах, связанных с изменением неупорядоченности, невозможно достигнуть абсолютного нуля (0К, или -273,15 С). Можно только бесконечно приближаться к этой температуре. Ученые договорились, что при 0 К неупорядоченность равна 0.

Важно! Абсолютное значение неупорядоченности можно посчитать как изменение энергии при данной температуре.

В термодинамике обычно не имеет значения абсолютная величина, важно только ее изменение. Однако можно найти и абсолютное значение. Оно вычисляется по разным формулам для твердого, жидкого и газообразного состояния вещества. Эта величина измеряется в Дж/К или Дж/градус, то есть в тех же единицах, что и теплоемкость. Удобно поделить эту величину на массу или количество моль вещества. Поэтому используют единицы Дж/(моль*К) или Дж/(моль*градус) в зависимости от того, в чем измеряется температура — в кельвинах или градусах.

Это интересно! Формулировки законов Исаака Ньютона: кратко и понятно

В химии

Что такое, к примеру, энтропия в химии? Это понятие применяется в химической термодинамике. Здесь важно изменение этой величины. Если оно положительно, то и система становится менее упорядоченной. Знать это важно для определения направления химических реакций и изменения химического равновесия. Этот термин связан с понятием энтальпии — энергии, которую можно превратить в тепло при определенном постоянном давлении.

По изменению неупорядоченности можно определить, может ли реакция протекать самопроизвольно. Этого нельзя сделать только по изменению энергии, так как существуют и реакции, протекающие с поглощением тепла, и реакции, протекающие с его выделением. Согласно второму началу термодинамики, состояние с наибольшей неупорядоченностью — это наиболее устойчивое состояние замкнутой системы. Также любая замкнутая система стремится к наименее упорядоченному состоянию. Поэтому при самопроизвольных процессах беспорядок возрастает.

Это интересно! Квантовые постулаты Нильса Бора: кратко об основных положениях

В теории информации

Информационная энтропия характеризует непредсказуемость какой-либо системы. Например, это может быть вероятность появления какого-то символа из алфавита в тексте. При этом эта функция равна количеству информации, которое приходится на один символ. Клод Шеннон — ученый, который ввел этот термин в теории информации, — даже сначала хотел называть эту величину информацией.

Шеннон предположил, что, увеличивая количество информации, мы уменьшаем неопределенность. Упорядочивая систему, мы также уменьшаем неопределенность.

Важно! Чем более предсказуемо какое-то событие, тем оно менее информативно, и тем меньше беспорядок.

С помощью этой неопределенности можно предсказывать события, например, исход какого-то эксперимента. Для этого события делят на отдельные части и считают неопределенность для них.

Информационная энтропия связана с числом доступных состояний. Чем это число больше, тем она больше. Например, если мы будем играть в шахматы по правилам, для шахматной доски эта величина будет меньше, чем если переставлять фигуры хаотически. Неопределенность для монетки, которая может упасть только на одну или другую сторону, меньше, чем у игральной кости с 6 гранями, а у кости с 20 гранями эта величина еще больше.

Существует также энтропия языка. Это понятие обозначает количество информации на единицу текста на этом языке (одни символ) и измеряется в битах на букву. Для разных языков она разная.

В языке одни символы появляются чаще, другие реже, также есть определенные часто встречающиеся сочетания символов. Проводя анализ вероятности появления того или иного символа, можно декодировать зашифрованный текст. Информационная неупорядоченность также помогает устанавливать необходимую пропускную способность каналов для передачи зашифрованных сообщений.

Для анализа данных в самых разных сферах, от медицины до социологии, используется информационно-энтропийный анализ. Простыми словами можно сказать, что, анализируя увеличение или уменьшение беспорядка, можно установить связи между явлениями.

Понятие «информационная энтропия» используется также в математической статистике и статистической физике. Эти науки также имеют дело с вероятностью различных состояний и используют методы теории вероятности.

Это интересно! Какие бывают системы отсчета в физике и что это такое

В экономике

В экономике используется понятие «коэффициент энтропии». Он связан с концентрацией продавцов на рынке. Чем больше концентрация, тем меньше этот коэффициент, или индекс. Он зависит от распределения долей между фирмами на рынке, и чем больше разница в величине этих долей, тем больше и коэффициент энтропии.

Если поделить этот индекс на количество фирм на рынке, получится относительный показатель. Он обозначается буквой Е. Его значение находится между 0 и 1. Значение Е=0 соответствует монополии, а Е=1 — совершенной конкуренции.

Что говорит википедия

В википедии можно найти разные определения этого понятия. Самое общее — это мера необратимого рассеяния энергии, отклонения реального процесса от идеального. Также в википедии можно найти:

статьи об этом термине в классической термодинамике,
в биологической экологии,
энтропию Вселенной,
языка,
дифференциальную,
топологическую,
информационную.

Полезное видео: представление об энтропии

Заключение

Термин «энтропия» впервые был использован в термодинамике Рудольфом Клаузиусом. Из физики он пришел и в другие науки. Это понятие обозначает неупорядоченность, хаотичность, непредсказуемость и тесно связано с вероятностью. Энтропийный анализ помогает изучать данные и находить связи между явлениями, определять направления физических и химических процессов.

что это такое простыми словами

И физики, и лирики оперируют понятием «энтропия». В переводе с древнегреческого языка на русский слово «энтропия» связывают с поворотом, превращением.

Представители точных наук (математики и физики) ввели данный термин в научный обиход и распространили его на информатику, химию. Р. Клаузиус, и Л. Больцман, Э. Джейнс и К. Шеннон, К. Юнг и М.Планк определяли и исследовали названное выше явление.

В данной статье обобщаются, систематизируются основные подходы к определению энтропии в различных научных областях.

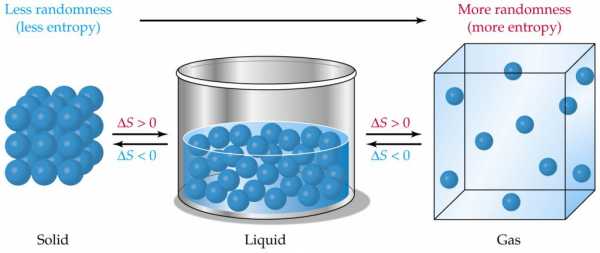
Энтропия в точных и естественных науках

Начиная с представителя точных наук Р.Клаузиса, термином «энтропия» обозначают меру:

необратимого рассеивания энергии в термодинамике;
вероятности осуществления какого-либо макроскопического процесса в статистической физике;
неопределенности какой-либо системы в математике;
информационной ёмкости системы в информатике.

Данная мера выражается формулами и графиками.

Энтропия, как гуманитарное понятие

К. Юнг ввел знакомое нам понятие в психоанализ, изучая динамику личности. Исследователи в области психологии, а затем и социологии выделяют и определяют энтропию личности или социальную энтропию как степень:

неопределенности состояния личности в психологии;
психической энергии, которую нельзя использовать при вложении её в объект исследования в психоанализе;
количества энергии, недоступной для социальных изменений, социального прогресса в социологии;
динамика энтропии личности.

Понятие энтропии оказалось востребованным, удобным в теориях, как естественнонаучных, так и гуманитарных. В целом энтропия тесно связана с мерой, степенью неопределенности, хаоса, беспорядка в любой системе.