Фибоначчи что это такое

Фибоначчи — Википедия

Леона́рдо Пиза́нский (лат. Leonardus Pisanus, итал. Leonardo Pisano, около 1170 года, Пиза — около 1250 года, там же) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи.

Отец Фибоначчи по торговым делам часто бывал в Алжире, и Леонардо изучал там математику у арабских учителей. Позже Фибоначчи посетил Египет, Сирию, Византию, Сицилию. Он ознакомился с достижениями античных и индийских математиков в арабском переводе. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки. Труд Леонардо Фибоначчи «Книга абака» способствовал распространению в Европе позиционной системы счисления, более удобной для вычислений, чем римская нотация; в этой книге были подробно исследованы возможности применения индийских цифр, ранее остававшиеся неясными, и даны примеры решения практических задач, в частности, связанных с торговым делом ^[1]. Позиционная система приобрела в Европе популярность в эпоху Возрождения^[2].

Сам Леонардо Пизанский никогда не называл себя «Фибоначчи». Первое известное нам упоминание «Леонардо Фибоначчи» (Lionardo Fibonacci) содержится в записях нотариуса Священной Римской империи Перизоло (Perizolo da Pisa, Notaro Imperiale) за 1506 год^[3][4]. Слово Fibonacci — сокращение от двух слов «filius Bonacci», появившихся на обложке «Книги абака»; они могли означать либо «сын Боначчо», либо, если интерпретировать слово Боначчи как фамилию, «сын Боначчи». Согласно третьей версии, само слово Боначчи нужно тоже понимать как прозвище, означавшее «удачливый». Сам он обычно подписывался Боначчи; иногда он использовал также имя Леонардо Биголло — слово bigollo на тосканском наречии значило «странник», а также «бездельник»^[5].

Фибоначчи родился в итальянском городе Пиза, предположительно в 1170-е годы (в некоторых источниках стоит 1180 год). Его отец, Гильермо, был торговцем. В 1192 году он был назначен представлять пизанскую торговую колонию в Северной Африке и часто бывал в Беджаи, Алжир. По желанию отца, который хотел, чтобы Леонардо стал хорошим торговцем, он переехал в Алжир и изучал там математику (искусство вычислений) у арабских учителей. Позже Фибоначчи посетил Египет, Сирию, Византию, Сицилию ^[6].

В 1200 году Леонардо вернулся в Пизу и принялся за написание своего первого труда «Книги абака»^[6]. В то время в Европе о позиционной системе счисления и арабских цифрах знали очень немногие. В своей книге Фибоначчи всячески поддерживал индийские приёмы вычисления и методы^[7]. По словам историка математики А. П. Юшкевича, «„Книга абака“ резко возвышается над европейской арифметико-алгебраической литературой XII—XIV веков разнообразием и силой методов, богатством задач, доказательностью изложения… Последующие математики широко черпали из неё как задачи, так и приёмы их решения». По первой книге многие поколения европейских математиков изучали индийскую позиционную систему счисления^[7].

Книга заинтересовала императора Фридриха II и его придворных, среди которых был астролог Майкл Скот(Michael Scotus), философ Теодорус Физикус (Theodorus Physicus) и Доминикус Хиспанус (Dominicus Hispanus). Последний предложил, чтобы Леонардо пригласили ко двору в одно из посещений императором Пизы около 1225 года, где ему задавал задачи Иоган Палермский, ещё один придворный философ Фридриха II. Некоторые из этих задач появились в последующих работах Фибоначчи ^[5][8]. Благодаря хорошему образованию Леонардо удалось обратить на себя внимание императора Фридриха II во время математических турниров. Впоследствии Леонардо пользовался покровительством императора^[9].

Несколько лет Фибоначчи жил при дворе императора. К этому времени относится его работа «Книга квадратов», написанная в 1225 году. Книга посвящена диофантовым уравнениям второй степени и ставит Фибоначчи в один ряд с такими учёными, развивавшими теорию чисел, как Диофант и Ферма^[8]. Единственное упоминание о Фибоначчи после 1228 года относится к 1240 году, когда ему в Пизанской республике была назначена пенсия за заслуги перед городом^[5].

Прижизненных портретов Фибоначчи не сохранилось, а существующие являются современными представлениями о нём. Леонардо Пизанский не оставил практически никаких автобиографических сведений; единственным^[10] исключением является второй абзац «Книги абака», где Фибоначчи излагает причины, побудившие его написать книгу:

Когда отцу моему была назначена должность таможенного чиновника, заведовавшего в Беджайе делами стекавшихся к нему пизанских торговцев, он в отрочестве моём призвал меня к себе и предложил несколько дней учиться счётному искусству, сулившему немало удобств и выгод для моего будущего. Наученный благодаря мастерству учителей основам индийского счёта, я приобрёл большую любовь к этому искусству и заодно узнал, что кое-что об этом предмете известно среди египтян, сирийцев, греков, сицилийцев и провансальцев, развивших свои методы. Позже, во время торговых путешествий по всем этим краям, я посвятил много труда подробному изучению их методов и, кроме того, овладел искусством научного спора. Однако по сравнению с методом индийцев все построения этих людей, включая подход алгорисмиков и учение Пифагора, кажутся почти заблуждениями, а потому я решил, изучив как можно внимательнее индийский метод, изложить его в пятнадцати главах настолько понятно, насколько смогу, с добавлениями от собственного разума и с кое-какими полезными примечаниями из геометрии Евклида, вставленными по ходу сочинения. Дабы пытливый читатель мог изучить индийский счёт наиболее вдумчивым образом, я сопроводил почти каждое утверждение убедительным доказательством; рассчитываю, что латинский народ отныне не будет лишён самых точных сведений об искусстве вычислений. Если же, паче чаяния, я пропустил что-то более или менее важное, а может быть, необходимое, то молю о прощении, ибо нет среди людей никого, кто был бы безгрешен или обладал способностью всё предвидеть.

Оригинальный текст (лат.)

Cum genitor meus a patria publicus scriba in duana bugee pro pisanis mercatoribus ad eam confluentibus constitutus preesset, me in pueritia mea ad se venire faciens, inspecta utilitate et commoditate futura, ibi me studio abbaci per aliquot dies stare voluit et doceri. Vbi ex mirabili magisterio in arte per novem figuras indorum introductus, scientia artis in tantum mihi pre ceteris placuit, et intellexi ad illam quod quicquid studebatur ex ea apud egyptum, syriam, greciam, siliciam, et provinciam cum suis variis modis, ad que loca negotiationis causa postea peragravi per multum studium et disputationis didici conflictum. Sed hoc totum etiam, et algorismum atque artem pictagore quasi errorem computavi respectu modi indorum. Quare, amplectens strictius ipsum modum indorum et attentius studems in eo, ex proprio sensu quedam addens et quedem etiam ex subtilitatibus euclidis geometrice artis apponens, summam huius libri, quam intelligibilius potui, in quindecim capitulis distinctam componere laboravi, fere omnia que inserui certa probatione ostendens, ut extra perfecto pre ceteris modo hanc scientiam appetentes instruantur, et gens latina de cetero, sicut hactenus, absque illa minime inveniatur. Si quid forte minus aut plus iusto vel necessario intermisi, mihi deprecor indulgeatur, cum nemo sit qui vitio careat et in omnibus undique sit circumspectus.

Однако точный смысл этого абзаца нельзя считать полностью известным, потому что его текст, как и весь латинский текст книги, дошёл до нас с ошибками, внесёнными переписчиками.^[11][12]

Значительную часть усвоенных им знаний он изложил в своей «Книге абака» (Liber abaci, 1202 год; до наших дней сохранилась только дополненная рукопись 1228 года)^[2]. Эта книга состоит из 15 глав и содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной. Первые пять глав книги посвящены арифметике целых чисел на основе десятичной нумерации. В VI и VII главе Леонардо излагает действия над обыкновенными дробями. В VIII—X главах изложены приёмы решения задач коммерческой арифметики, основанные на пропорциях. В XI главе рассмотрены задачи на смешение. В XII главе приводятся задачи на суммирование рядов — арифметической и геометрической прогрессий, ряда квадратов и, впервые в истории математики, возвратного ряда, приводящего к последовательности так называемых чисел Фибоначчи. В XIII главе излагается правило двух ложных положений и ряд других задач, приводимых к линейным уравнениям. В XIV главе Леонардо на числовых примерах разъясняет способы приближённого извлечения квадратного и кубического корней. Наконец, в XV главе собран ряд задач на применение теоремы Пифагора и большое число примеров на квадратные уравнения. Леонардо впервые в Европе использовал отрицательные числа, которые рассматривал как долг^[7]. Книга посвящена Майклу Скоту^[5].

Другая книга Фибоначчи, «Практика геометрии» (Practica geometriae, 1220 год), состоит из семи частей и содержит разнообразные теоремы с доказательствами, относящиеся к измерительным методам. Наряду с классическими результатами Фибоначчи приводит свои собственные — например, первое доказательство того, что три медианы треугольника пересекаются в одной точке (Архимеду этот факт был известен, но если его доказательство и существовало, до нас оно не дошло). Среди землемерных приёмов, которым посвящён последний раздел книги, — использование определённым образом размеченного квадрата для определения расстояний и высот. Для определения числа π{\displaystyle \pi } Фибоначчи использует периметры вписанного и описанного 96-угольника, что приводит его к значению 3,1418{\displaystyle 3,1418}^[7]. Книга была посвящена Доминикусу Хиспанусу^[5]. В 1915 году Р. С. Арчибальд занимался восстановлением утерянной работы Евклида о делении фигур, базируясь на «Практике геометрии» Фибоначчи и французском переводе арабской версии^[11].

В трактате «Цветок» (Flos, 1225 год) Фибоначчи исследовал кубическое уравнение x3+2x2+10x=20{\displaystyle x^{3}+2x^{2}+10x=20}, предложенное ему Иоанном Палермским на математическом состязании при дворе императора Фридриха II^[7]. Сам Иоанн Палермский почти наверняка заимствовал это уравнение из трактата Омара Хайяма «О доказательствах задач алгебры», где оно приводится как пример одного из видов в классификации кубических уравнений. Леонардо Пизанский исследовал это уравнение, показав, что его корень не может быть рациональным или же иметь вид одной из квадратичных иррациональностей, встречающихся в X книге Начал Евклида, а затем нашёл приближённое значение корня в шестидесятеричных дробях, равное 1;22,07,42,33,04,40^[8], не указывая, однако, способа своего решения^[5].

«Книга квадратов» (Liber quadratorum, 1225 год) содержит ряд задач на решение неопределённых квадратных уравнений. Фибоначчи работал над поиском чисел, которые, будучи добавленными к квадратному числу, вновь дадут квадратное число. Он отметил, что числа x2+y2{\displaystyle x^{2}+y^{2}} и x2−y2{\displaystyle x^{2}-y^{2}} не могут быть квадратными одновременно^[8], а также использовал для поиска квадратных чисел формулу x2+(2x+1)=(x+1)2{\displaystyle x^{2}+(2x+1)=(x+1)^{2}}^[5]. В одной из задач книги, также первоначально предложенной Иоанном Палермским, требовалось найти рациональное квадратное число, которое, будучи увеличено или уменьшено на 5, вновь даёт рациональные квадратные числа^[7].

Среди не дошедших до нас произведений Фибоначчи трактат Di minor guisa по коммерческой арифметике, а также комментарии к книге X «Начал» Евклида^[5].

Оставаясь верным математическим турнирам, основную роль в своих книгах Фибоначчи отводит задачам, их решениям и комментариям. Задачи на турниры предлагал как сам Фибоначчи, так и его соперник, придворный философ Фридриха II Иоган Палермский^[9]. Задачи Фибоначчи, как и их аналоги, продолжали использовать в различных математических учебниках несколько столетий. Их можно встретить в «Сумме арифметики» Пачиоли (1494), в «Приятных и занимательных задачах» Баше де Мизириака (1612), в «Арифметике» Магницкого (1703), в «Алгебре» Эйлера (1768)^[2].

Задача о размножении кроликов[править | править код]

В место, огороженное со всех сторон стеной, поместили пару кроликов, природа которых такова, что любая пара кроликов производит на свет другую пару каждый месяц, начиная со второго месяца своего существования. Сколько пар кроликов будет через год? (Ответ: 233 пары). Для поиска ответа используется рекуррентная числовая последовательность 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, … (по ней составлена последовательность A000045 в OEIS; отличие в том, что вторая последовательность начинается с нуля и единицы, а не с единицы и двойки), в которой каждое последующее число равно сумме двух предыдущих; ответом, в соответствии с условиями задачи, является тринадцатый член (завершение каждого месяца — это перескок к следующему члену последовательности; текущий член последовательности перед началом опыта — это первый; всего месяцев двенадцать). В честь учёного она носит название чисел Фибоначчи. Числа Фибоначчи нашли своё применение во многих областях математики. Одним из важных свойств последовательности является тот факт, что предел отношения an+1{\displaystyle a_{n+1}} к an{\displaystyle a_{n}} равен золотому сечению^[2]. Наглядно формирование последовательности можно показать следующим образом:

1: 1 + 1 = 2 2: 1 + 2 = 3 3: 2 + 3 = 5 4: 3 + 5 = 8 5: 5 + 8 = 13 6: 8 + 13 = 21 7: 13 + 21 = 34 8: 21 + 34 = 55 9: 34 + 55 = 89 ... и т. д. 

Задачи о гирях[править | править код]

Задача о выборе наилучшей системы гирь для взвешивания на рычажных весах^[13][14] впервые была сформулирована именно Фибоначчи. Леонардо Пизанский предлагает два варианта задачи:

• Простой вариант: требуется найти пять гирь, с помощью которых можно найти все веса меньше 30, при этом гири можно класть только на одну чашу весов (Ответ: 1, 2, 4, 8, 16). Решение строится в двоичной системе счисления^[2].
• Сложный вариант: требуется найти наименьшее число гирь, с помощью которого можно взвесить все веса меньше заданного (Ответ: 1, 3, 9, 27, 81,…). Решение строится в системе счисления по основанию три^[2] и в общем случае представляет собой последовательность A000244 в OEIS.

Задачи по теории чисел[править | править код]

Кроме задачи о кроликах, Фибоначчи предлагал ряд других задач по теории чисел^[11]:

• Найти число, которое делится на 7 и даёт в остатке единицу при делении на 2, 3, 4, 5 и 6; (Ответ: 301)
• Найти число, произведение которого с семёркой даёт остатки 1, 2, 3, 4, 5 при делении на 2, 3, 4, 5, 6, соответственно;
• Найти квадратное число (то есть число, равное квадрату целого числа), которое при увеличении или уменьшении на 5 давало бы квадратное число.

Некоторые другие задачи[править | править код]

• Найти число, 19/20 которого равно квадрату самого числа. (Ответ: 19/20)^[2].
• Сплав из 30 весовых частей состоит из трёх металлов: первый металл достоинством по три монеты на одну часть, второй металл по две монеты на одну часть, а у третьего металла каждые две части стоят по одной монете; стоимость всего сплава 30 монет. Сколько частей каждого металла содержит сплав? (Ответ: 3 части первого металла, 5 частей второго металла, 22 части третьего). В таких терминах Фибоначчи переформулировал известную задачу о птицах, в которой были использованы те же самые числа (30 птиц трёх разных видов стоят 30 монет, по заданным ценам найти количество птиц каждого вида)^[7].
• «Шуточная задача о семи старухах», которые шли в Рим, и у каждой было по семь мулов, на каждом из которых по семь мешков, в каждом из которых по семь хлебов, в каждом из которых по семь ножей, каждый из которых в семи ножнах. Нужно найти общее число предметов. Эта задача обошла много стран, первое известное упоминание о ней было ещё в Древнем Египте в папирусе Ахмеса. (Ответ: 137 256)^[2][7].

Памятник Фибоначчи в Пизе

В XIX веке в Пизе был поставлен памятник учёному. Ранее статуя стояла в Giardino Scotto, а после того, как в 1978 году Франк Джонсон нарисовал портрет Фибоначчи с этой статуи, она была перенесена на кладбище Кампосанто, расположенном в Пизе на Пьяцца деи Мираколи.

Именем Фибоначчи названы улицы в Пизе (Lungarno Fibonacci) и во Флоренции (Via Fibonacci). Кроме того, имя Фибоначчи носит ассоциация Fibonacci Association^[15] и издаваемый ею научный журнал Fibonacci Quarterly^[16], посвящённые числам Фибоначчи, проект Евросоюза в сфере образования^[17], а также другие программы^[11].

При покровительстве императора Леонардо Пизанский написал несколько книг^[18][5][9]:

• «Книга абака» (Liber abaci), 1202 год, дополнена в 1228 году;
• «Практика геометрии» (Practica geometriae), 1220 год;
• «Цветок» (Flos) 1225 год;
• «Книга квадратов» (Liber quadratorum), 1225 год;
• Di minor guisa, утеряно;
• Комментарии к книге X «Начал» Евклида, утеряно;
• Письмо Теодорусу, 1225 год.

1. ↑ N. Ambrosetti. L'eredità arabo-islamica nelle scienze e nelle arti del calcolo dell'Europa. — LED Edizioni Universitarie, 2008. — С. 220—221.
2. ↑ ^{1 2 3 4 5 6 7 8} Карпушина Н. «Liber abaci» Леонардо Фибоначчи, Математика в школе, № 4, 2008.
3. ↑ Drozdyuk, Andriy; Drozdyuk, Denys. Fibonacci, his numbers and his rabbits. — Toronto: Choven Pub, 2010. — С. 18. — xi, 129 с. — ISBN 978-0-9866300-1-9, 0-9866300-1-2.
4. ↑ Дроздюк А. В.; Дроздюк Д. В. Фибоначчи, его числа и кролики. Пер. с англ. — Торонто: Choven, 2010. — С. 20. — 145 с. — ISBN 978-0-9866300-0-2.
5. ↑ ^{1 2 3 4 5 6 7 8 9} Leonardo Pisano Fibonacci
6. ↑ ^{1 2} R.Knott, D.A.Quinney and PASS Maths The life and numbers of Fibonacci
7. ↑ ^{1 2 3 4 5 6 7 8} История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. I: С древнейших времён до начала Нового времени. — С. 260—267.
8. ↑ ^{1 2 3 4} Frances Carney Gies Leonardo Pisano//Энциклопедия Британника
9. ↑ ^{1 2 3} Яглом И. М. Итальянский купец Леонардо Фибоначчи и его кролики. // Квант, 1984. № 7. С. 15-17
10. ↑ [1] Treccani, l’Enciclopedia Italiana: Fibonacci, Leonardo (detto Leonardo Pisano)
11. ↑ ^{1 2 3 4} EIGHT HUNDRED YEARS YOUNG// A. F. HORADAM
12. ↑ RICHARD E.GRIMM//THE AUTOBIOGRAPHY OF LEONARDO PISANO
13. ↑ А. П. Стахов. Две знаменитые задачи Фибоначчи http://www.goldenmuseum.com/1001TwoProblems_rus.html Архивная копия от 16 декабря 2010 на Wayback Machine
14. ↑ Леонардо Пизано Фибоначчи http://www.xfibo.ru/fibonachi/leonardo-pisano-fibonacci.htm Архивная копия от 8 апреля 2014 на Wayback Machine
15. ↑ The Fibonacci Association Архивировано 8 июня 2007 года.
16. ↑ Fibonacci Quarterly
17. ↑ Fibonacci Project
18. ↑ A brief biographical sketch of Fibonacci, his life, times and mathematical achievements.

• Щетников А. И. К реконструкции итерационного метода решения кубических уравнений в средневековой математике. Труды третьих Колмогоровских чтений. Ярославль: Изд-во ЯГПУ, 2005, с. 332—340.
• Glushkov S. On approximation methods of Leonardo Fibonacci. Historia Mathematica, 3, 1976, p. 291—296.
• Sigler, L. E. Fibonacci’s Liber Abaci, Leonardo Pisano’s Book of Calculations" Springer. New York, 2002, ISBN 0-387-40737-5.

Число Бога, числа Фибоначчи, Золотое Сечение

Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать.

Первая тысяча знаков значения Φ

1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362

Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.

Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел.

Свидетельства использования древними мыслителями золотой пропорции приведены в книге Эвклида «Начала», написанной еще в 3 в. до н.э., который применял это правило для построения правильных 5-угольников. У пифагорейцев эта фигура считается священной, поскольку является одновременно симметричной и асимметричной. Пентаграмма символизировала жизнь и здоровье.

Числа Фибоначчи

Знаменитая книга Liber abaci математика из Италии Леонардо Пизанского, который в последующем стал известен, как Фибоначчи, увидела свет в 1202 г. В ней ученый впервые приводит закономерность чисел, в ряду которых каждое число является суммой 2-х предыдущих цифр. Последовательность чисел Фибоначчи заключается в следующем:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.

Также ученый привел ряд закономерностей:

Любое число из ряда, разделенное на последующее, будет равно значению, которое стремится к 0,618. Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным.

Если же поделить число из ряда на предыдущее, то результат устремится к 1,618.

Одно число, поделенное на следующее через одно, покажет значение, стремящееся к 0,382.

Применение связи и закономерностей золотого сечения, числа Фибоначчи (0,618) можно найти не только в математике, но и в природе, в истории, в архитектуре и строительстве и во многих других науках.

Для практических целей ограничиваются приблизительным значением Φ = 1,618 или Φ = 1,62. В процентном

Что такое числа Фибоначчи и почему их выделили в отдельную группу чисел?

Числа Фибоначчи в Европе популяризовал Леонардо Пизанский (по прозвищу Фибоначчи – сын Боначчи), в задаче о кроликах:

Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов (самку и самца) в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения.

Оказывается, число кроликов по месяцам описывается последовательностью

1, 2, 3, 5, 8, 13,…

В ней каждое число равно сумме двух предыдущих. Условия задачи все равно нереалистичны, так что можно не стесняться: предположить, что кролики бессмертны, и продолжить последовательность до бесконечности:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, ….

Есть свидетельства, что последовательность задолго до Леонардо была известна в Индии, и что в честь Фибоначчи ее назвал Эдуард Люка.

Про экспоненциальный рост

Как мы видим, последовательность очень быстро растет (экспоненциально, как последовательность степеней). Примерно как 1, 2, 4, 8, 16, 32, … или 1, 10, 100, 1000, … (тоже экспоненциальный рост.) Экспоненциальный рост вообще встречается в природе и в приложениях: так растут популяции, капиталы в банке, число радиоактивных атомов и число зерен на шахматной доске (Вы же помните легенду про жадного султана и бедного изобретателя шахмат ;))

В природе экспоненциальный рост имеет место лишь приблизительно и только в некоторых пределах.

Красивые фотографии

Последовательности в природе, напоминающие Фибоначчи, тоже похожи на Фибоначчи только приблизительно и в некоторых пределах. Широко известны примеры из мира растений: семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса. Видимо, здесь задействован один механизм (я скопировала первую попавшуюся картинку из интернета):

Отчасти популярность чисел Фибоначчи связана с такими красивыми картинками. В интернете их полным-полно.

А вот скажем, закон радиоактивного распада не менее поразителен, история его открытия драматична, человечество поставило его себе на службу… но он не так популярен в СМИ. Нет для него таких красивых картинок, да и описывается он дифференциальным уравнением, а любителей дифференциальных уравнений меньше, чем любителей красивых картинок.

В математике

В математике бывают объекты, которые задаются очень просто, но показывают удивительно сложные и многогранные связи между своими компонентами. Например: треугольник в планиметрии, конические сечения, треугольник Паскаля, простые числа, … Они завораживают нас как картинки в калейдоскопе. Чуть повернешь – и открываются новые узоры, новые свойства. Числа Фибоначчи –один из таких объектов. Каждый математик на пути в науку их обязательно встречал.

Чтобы перечислить все их удивительные свойства, нужна отдельная книга (и кстати, выходит журнал с таким названием, посвященный одним только числам Фибоначчи). Скажу только, что отношение каждого числа Фибоначчи к предыдущему приближает золотое сечение, и чем числа больше, тем приближение лучше.

Почему же математики выделили числа Фибоначчи в отдельную группу чисел

Потому что любят все классифицировать и раскладывать по полочкам. Раз есть объект – надо дать ему название. На сайте https://oeis.org/A000045 , где собраны большинство последовательностей чисел, встречающихся в математике, последовательность Фибоначчи идет под номером 45. Она вовсе не такая уж исключительная, кроме неё на этом сайте собрано около трети миллиона последовательностей. Каждая из них тоже представляет собой «отдельную группу чисел».

Специалист по теории чисел Леопольд Кронекер считал, что только одна из них создана Богом (и это вовсе не последовательность Фибоначчи, а другая, на сайте ее номер 27), а остальные – дело рук человеческих.

В целом журналисты несколько преувеличивают значимость чисел Фибоначчи: они, безусловно, прекрасны, но стоят в одном ряду с многими другими не менее прекрасными и полезными математическими объектами.

Фибоначчи повсюду! - Мастерок.жж.рф — LiveJournal

Итак, мы выяснили с вами Кто такой Фибоначчи, а теперь давайте рассмотрим вот такой феномен.

Оказывается Фибоначчи повсюду!

На самом деле эти числа были известны задолго до Фибоначчи ещё в древней Индии, где они использовались в метрическом стихосложении.

Леонардо Фибоначчи первым ввёл эту числовую последовательность в западноевропейской математической науке в своей важной книге «Liber Abaci» («Книга абака») в 1202 году. Он использовал эту последовательность чисел, когда пытался объяснить рост популяции кроликов.

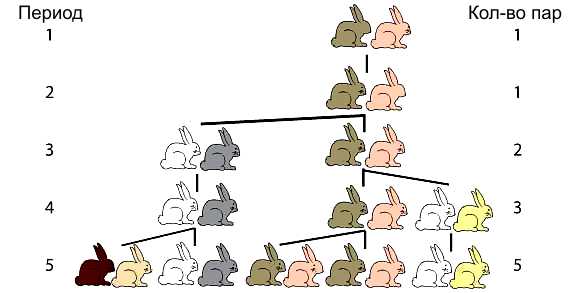
Фибоначчи рассматривает гипотетическую ситуацию, когда в поле появляется пара кроликов. Они спариваются в конце месяца и в конце второго месяца самка производит еще одну пару. Кролики никогда не умирают, спариваются ровно через месяц, и самки всегда производят пару (один самец, одна самка). Вопрос, который поставил Фибоначчи был следующим: сколько пар будет через один год? Если посчитать, то окажется, что количество пар в конце N-го месяца равно Fn или N-му числу Фибоначчи. Таким образом, количество пар кроликов через 12 месяцев будет F12 или 144.

Числа Фибоначчи и золотое сечение

Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».

Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.

Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.
Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.

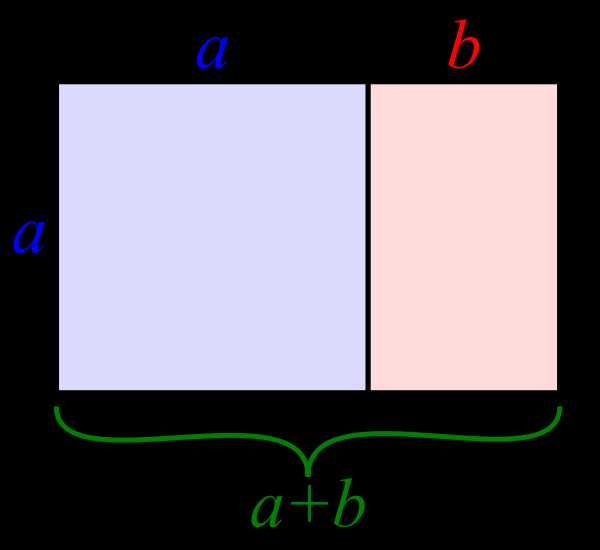
Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.

Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.

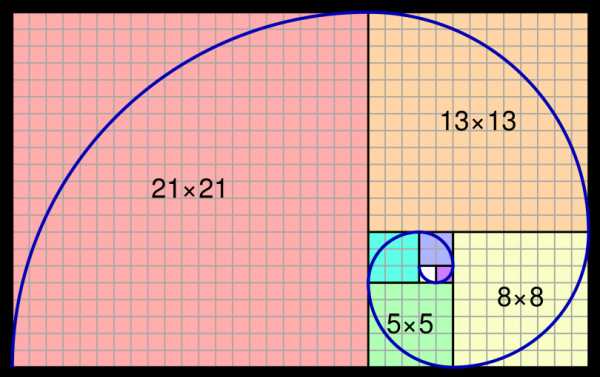
Почему эта последовательность настолько уникальна
Числа Фибоначчи описывают различные явления в искусстве, музыке и природе. Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи. Длины и ширины много прямоугольных предметов, таких как учетные карточки, окна, игральные карты и пр. соответствуют последовательным числам ряда Фибоначчи.

Числа Фибоначчи в природе

Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.

Последовательность Фибоначчи можно также увидеть в форме или разделении ветвей дерева. Основной ствол будет расти до тех пор, пока он не создаст ветвь, которая создает две точки роста. Затем один из новых стеблей разветвляется на два, в то время как другой находится в состоянии покоя. Такая картина ветвления повторяется для каждого из новых стеблей. Корневая система и даже водоросли также демонстрируют эту закономерность.

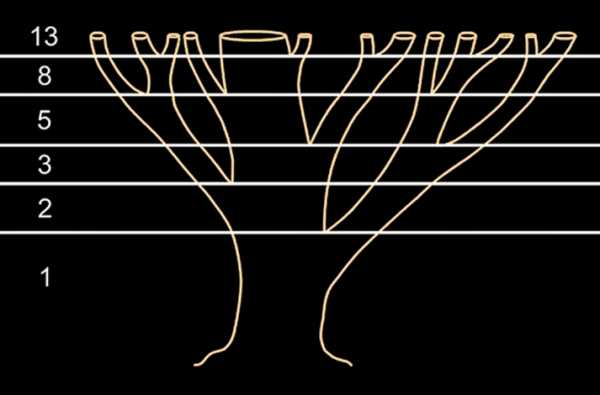
Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.

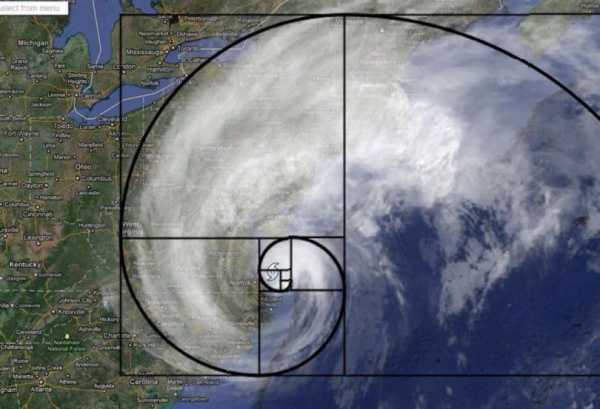
Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов.

Числа Фибоначчи в теле человека

Есть много примеров соотношений частей тела человека на основе последовательности Фибоначчи, например рука и, в частности, кости пальца.

Каждая кость указательного пальца, от кончика до основания запястья, больше предыдущей примерно на коэффициент Фибоначчи 1,618, что соответствует числам Фибоначчи 2, 3, 5 и 8.

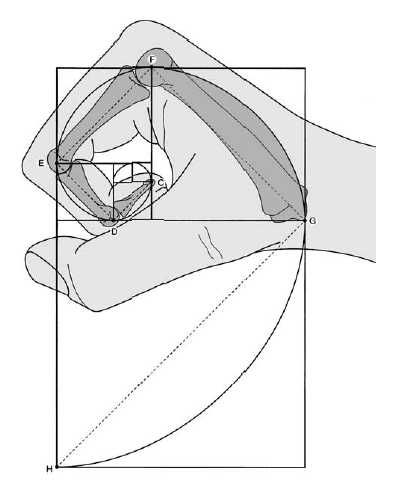
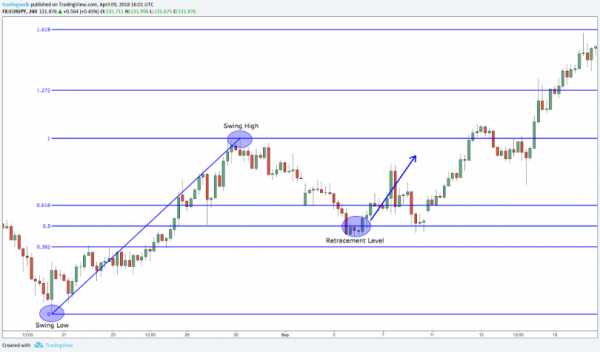
Числа Фибоначчи в биржевой торговле

Последовательность Фибоначчи является инструментом технического анализа, используемым профессиональными трейдерами в сочетании с другими инструментами для расчета прогноза потенциального конца коррекции, принимая процент от предыдущего движения.

Считается, что во время мощного рыночного движения, цены могут откатываться на 23,6% (это соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+3), 38,2% (соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+2) или 50% (половина). Эти уровни коррекции Фибоначчи считаются «нормальными». Если же цена падает на 61,2% (отношение двух соседних чисел ряда Фибоначчи — позиции N и N+1) и более, то это серьезный сигнал вероятного разворота тренда.

Числа Фибоначчи в фотографии и искусстве

В фотографии сетка фи (phi) является интерполяцией спирали Фибоначчи и в наши дни считается фундаментальным методом для создания приятной композиции в кадре. Цель состоит в том, чтобы выровнять объект по линиям, созданным спиралью, или использовать её в качестве разделителя для создания правильного ощущения кадра.

Сетка фи (красные линии) и спираль Фиббоначи в кадре.

Имеется много примеров, когда последовательность Фибоначчи появляется вокруг нас, и мы не обращаем внимания на это математическое чудо, которое кажется таинственным фактором, приносящим универсальную форму гармонии элементам математического музыкального искусства природы.

Может именно из-за этого Дональд Трамп был избран президентом? (шутка):

И еще немного фундаментального числа!

[источники]
Источники:
View story at Medium.com

Это копия статьи, находящейся по адресу http://masterokblog.ru/?p=47272.

Уровни Фибоначчи в трейдинге

Рыночная цена тяготеет к уровням — и это понятно, ведь именно на уровнях находится скопление рыночных ордеров. Поэтому есть несколько техник прогнозирования этих уровней, от простых п/с до чрезвычайно популярных чисел Фибоначчи, что встречаются буквально на каждом 3м графике. Существует колоссальное количество торговых систем на их основе, однако, все из них можно распределить по двум темам: коррекции (ретрейсменты) и расширения.

Леонардо Фибоначчи — древний итальянский кекс, что обнаружил простую числовую последовательность. Эта последовательность, как выяснилось, встречается повсеместно и является универсальной для множества природных явлений.

Выглядит она вот так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

Последовательность начинается с 0, затем 1, далее 0 + 1 = 1, третье число. К нему прибавляются второе и третье число последовательности (1 +1) = 2, четвертое число. К нему прибавляется третье и пошло-поехало.

Последовательность Фибоначчи — это сумма двух предыдущих чисел.

Далее, на основе двух чисел определяется любопытная пропорция. Если первое число в последовательности разделить на второе — следующее в ряду — получится 0.618. Скажем, если 55 разделить на 89 либо 21 разделить на 34. Всегда одна и та же пропорция, с округлением в бОльшую сторону. Всегда 0.618.

Если же делить числа через одно, будет всегда получится 0.382. Скажем, 13 / 34, либо 34 / 89 = 0.382. Магия и шаманство чисел.

Эти дроби считаются так называемым «золотым сечением» и оно встречается в природе повсеместно. Особенно любят в качестве примера показывать спирали, как в подсолнухе укладываются семечки и прочее. Эдакая вселенская дробь.

Теперь сразу к делу, чтобы долго эти дроби не мусолить.

Уровни коррекции (ретрейсемента) Фибоначчи выглядят вот так:

0.236, 0.382, 0.500, 0.618, 0.764

Уровни расширения Фибоначчи так:

0, 0.382, 0.618, 1.000, 1.382, 1.618

Хорошая новость — дроби вам считать не придется. Мало того, что есть калькуляторы, так и на живом графике они рисуются автоматически.

Зачем нужны уровни, основанные на их дробях? Многие трейдеры считают, что если семечки в подсолнухе идут по спирали, расстояние между ветвями которой вычисляется этими дробями, почему бы уровни ретрейсмента не использовать как поддержку или сопротивление? Вот трейдеры так их и используют. Эти уровни также применяются для открытия сделок или размещения стопов в форексе.

А вот уровни расширения используются в форексе для установки ордеров вроде «тейк-профит». Другими словами, по их мнению, цена частенько до этих уровней доходит, что и нужно принимать во внимание при анализе.

Фибоначчи на графике используется на основе свингов — это такие свечи, где слева и справа от них есть, как минимум, два верхних максимума либо верхних минимума. Сейчас покажем на примерах, ибо здесь легко запутаться.

Свечной свинговый паттерн выглядит вот так. Просто свечка и две свечи по бокам, что выше/ниже ее.

Уровни ретрейсмента (коррекции)

Сразу договоримся, уровни Фибоначчи — трендовый инструмент, для консолидации они не подходят. Суть в том, что когда тренд идет вверх, цена тяготеет к откатам от уровней сопротивления, построенных на дробях Фибоначчи. Аналогично для тренда вниз и поддержки.

Чтобы построить эти уровни, нам понадобятся свинги и сетка на живом графике. Нашли нижние свинги, затем верхние и протянули между ними сетку.

На живом графике выбрать ее можно вот так:

Фибоначчи в тренде вверх

Сетку мы протянули между этими двумя свечными моделями (свингами) и уровни ретрейсмента Фибоначчи показаны автоматически. Как видим, весь комплект присутствует.

Теперь возьмем дневной график AUD/USD и протянем нашу сетку между двумя свингами.

Основная задача — дождаться, пока цена не определится с уровнем поддержки от одного из ретрейсментов Фибоначчи. Выглядит это вот так.

В данном случае откат произошел от уровня 0.382 после того, как цена пробила первый уровень коррекции 0.236.

Фибоначчи в тренде вниз

Действуем точно также, протягиваем сетку между двумя свечными паттернами-свингами, но уже вниз. График EUR/USD, 4-часовой ТФ. Расчет на то, что раз цена откатывает вверх, то она столкнется с одним из уровней сопротивления Фибоначчи, поскольку общий тренд вниз очень сильный.

Смотрим, что случилось дальше.

Действительно пошел откат, рынок притормозил ниже уровня 0.382 – ранний намек на исчерпание сил быков. Наконец, на уровне 0.500 быки выдохлись и и уровень отработал как сопротивление. И вот эти два уровня — 0.382 и 0.500 частенько взаимодействуют друг с другом. Их основное предназначение — в роли временных поддержки и сопротивления.

Про п/с мы все уже знаем, так что не ждите, что цена, аки мячик, будет от этих уровней прыгать. Нет. Это, в первую очередь, зоны трейдерской заинтересованности. Поэтому цена на таких уровнях любить консолидироваться в микро-канальчики, прежде чем путешествовать дальше.

Когда уровни коррекции Фибоначчи не работают

Как вы прекрасно уже знаете, цена может пробить как поддержку, так и сопротивления. А значит, она аналогичным образом пробивает и уровни Фибоначчи.

Так что эти уровни — намек, но не железобетонная гарантия откатов и отскоков.

Вот, скажем, мы протянули сетку и все, вроде бы, у нас получается. Тренд нисходящий, цена застряла на уровне 0.500. Ну что ж, скажете вы, самое время входить на отскоке, верно? Сейчас отскочит и все девушки наши (или парни, если вы трейдер женского пола). А может, и печеньки в магазине.

Однако, посмотрим что произошло потом. О, вот тебе и номер. Цена и не думала разворачиваться от этого уровня — напротив, бодро пошла себе дальше.

Как выяснилось, здесь речь идет уже о долгосрочном развороте тренда, а ему уровень 0.500 оказался не указом.

Какие из этого можно сделать выводы? Уровни коррекции Фибоначчи, как и все в техническом анализе, требуют тщательной отработки и непрерывных уточнений, постоянной фильтрации. Весь технический анализ построен на вероятностях, а не гарантиях. Поэтому цена не всегда взаимодействует с этими уровнями так, как вам захочется.

Порой уровни пробиваются, иногда вместо 0.500 отскок происходит от 0.618 и масса других примеров. Иногда цене вообще эти уровни глубоко до лампочки. Цена, как таковая, перемещается от одних уровней к другим, и некоторые уровни для нее более значимы в определенный момент времени, а некоторые — менее.

Так что в использовании уровней Фибоначчи вам пригодятся все инструменты в вашем арсенале, о которых мы уже знаем. Инструменты, которыми мы фильтруем входы от уровней поддержки и сопротивления, не важно, Фибоначчи ли или обычные. Скажем, осцилляторы с их дивергенциями, паттерны прайс экшн и многое другое.

И вообще, давайте совместим уровни Фибоначчи с поддержкой и сопротивлением — хорошая мысль.

Уровни коррекции Фибоначчи и уровни поддержки/сопротивления

Мы уже поняли, что уровни Фибоначчи довольно-таки субъективны. И как и все в техническом анализе, просто так их использовать нельзя. Окей, не будем оставлять бедное золотое сечение с его подсолнухами в одиночестве и найдем ему помощь в основах технического анализа — обычных уровнях.

В данном случае, нам нужен усилитель уровней. Это когда обычная поддержка или сопротивления хорошо сочетается с каким-то уровнем или уровнями коррекции Фибоначчи.

Скажем, следующим образом.

Восходящий тренд, столько зеленых свечей.. все это очень мило, но где же входить? Тем более что цена явно пошла с низкой волатильностью. Сетку мы растянули и давайте добавим зеркальный уровень, где сопротивление стало поддержкой. Его видно очень хорошо. Заметьте, как он сочетается с уровнем 0.5.

Теперь нам надо дождаться взаимодействия цены с этим уровнем. Как видим, цена действительно всерьез восприняла этот уровень, он отработал как поддержка, не пустил цену дальше и она, вся такая разочарованная, рванула вверх.

Были там и напряженные моменты, скажем, когда цена длинной тенью устроила ложный пробой и всячески капризничала. Как вы уже понимаете, поддержка и сопротивление — в первую очередь, зоны интереса. Область, что вызывает у цены максимальную реакцию. Не в последнюю очередь по той причине, что все используют эти уровни. И, закономерно, чем больше институциональных трейдеров применяют уровни Фибоначчи, тем больше эти уровни влияют на поведение цены. Тут есть прямая зависимость. Именно по этой причине работают и простые уровни поддержки и сопротивления.

Гарантий, что эти уровни будут «пружинить» цену, конечно же нет, но нам гарантии и не нужны, а то мы не знаем, что их в трейдинге нет? Знаем прекрасно. Но вот зона, где за ценой нужно следить пристально — для этого уровни Фибоначчи подходят вполне себе.

Уровни Фибоначчи и линия тренда

Другой способ применения Фибоначчи — вместе с еще одним базовым инструментом технического анализа. А какой там инструмент у нас после поддержки и сопротивления идет? Правильно — линии тренда.

Именно в восходящем и нисходящем тренде многие трейдеры используют уровни коррекции Фибоначчи, так что совместить их с линиями тренда — то, что доктор прописал.

Взглянем на следующий график. Как видим, валютная пара идет в восходящем движении, линия тренда красивая и однозначная.

Надо покупать, раз такая пьянка, скажем, когда цена снова коснется линии тренда. Однако, давайте добавим уровни коррекции Фибоначчи и посмотрим, что получится. А получится более точная зона входа.

Используем два свинговых значения и наблюдаем за происходящем. Нас особенно интересуют уровни 0.500 и 0.618. Мы на них будем возлагать надежды, как на хорошие уровни поддержки. Наблюдаем.

Вот вам и пожалуйста — уровень 0.618 (61.8%) отработал как поддержка, причем в аккурат на линии тренда. Самое время входить на дальнейшее повышение тренда.

Два простых инструмента порой дают не менее простые результаты. Аналогично можно использовать уровни Фибоначчи с горизонтальными поддержкой и сопротивлением. В данном случае, Фибоначчи будет выступать как еще один способ фильтрации входов у уровней п/с.

Коррекция Фибоначчи и японские свечи

Мы уже соединяли уровни Фибоначчи с поддержкой и сопротивлением, а также с линиями тренда. Давайте не будем останавливаться и добавим в наше меню японские свечи.

Уровни Фибоначчи — они и в Африке уровни. По поведению японских свечей можно определять и характер движения цены у таких уровней.

Взглянем на такой вот пример:

Видим отчетливый нисходящий тренд вниз, правда цена явно притормозила. Этот тренд, он еще работает и если да — где в него входить? Воспользуемся уровнями коррекции и проверим.

Видим, как цена чешет себе вверх, вот дела, а где же нисходящий тренд, как-то не наблюдается. Последняя свеча вообще, полная бычья, у самого уровня 0.618. Не похоже, что он удержится. Наблюдаем дальше.

Сюрприз — цена не смогла пробить этот уровень. Мало того — мы видим образование красивейшей свечи доджи прямо у уровня 0.618. Вы и сами помните, что это и свеча сомнений и, в ряде случаев, свеча разворота. Вполне вероятно, что уровень устоял, а все трейдеры пожирают глазами этот доджи.

И хотя это не гарантия разворота, шансы — а в трейдинге все зависит от вероятностей — выглядят весьма недурно.

Как видим, кто воспользовался шансом, тот и молодец — цена обеспечила долгожданный разворот аж до нижней линии поддержки. Это один из примеров того, как уровни коррекции фибоначчи, вместе со свечами, дают необходимые намеки при торговле.

Работу от уровней нужно подтверждать, свечи для этого — первый кандидат. Добавим к ним паттерны price action – будет еще лучше. Другими словами, если при анализе свечных комбинаций у уровней фибоначчи расценивать их, как стандартные уровни поддержки и сопротивления, можно добиться весьма неплохих результатов.

Уровни расширения Фибоначчи

Теперь расширим наш Фибоначчи-инструментарий, для чего взглянем на восходящий тренд. Сначала мы, как обычно, протягиваем сетку обычных уровней коррекции. Как это делается, мы помним — от нижнего свинга к верхнему, где свинг — это свечной разворотный паттерн, указывающий на минимальные и максимальные значения цены.

Видим, что уровень 0.500 работает как сопротивление и, после трех неудачных попыток пробоя, цена отправляется в дальнейшее путешествие вверх, после чего пробивает наш самый верхний уровень от верхнего свинга.

А что дальше? Чтобы это выяснить, растягиваем сетку уровней расширения фибоначчи.

Дальше мы наблюдаем картину маслом:

• Цена дошла до уровня 0.618, что совпал с предыдущим верхним свингом.
• Откатилась до уровня 0.382, что отработал как поддержка.
• Пошла вверх и уткнулась в сопротивление на уровне 1.000.
• Спустя некоторое время сопротивлением стал уровень 1.618.

Как видим, уровни 0.618, 1.000 и 1.618 вполне себе отработали как поддержка и сопротивление, в нужных местах.

Теперь проделаем аналогичный трюк для нисходящего тренда. Используем тот же скриншот, что уже был немного раньше и делаем все точно также. Сначала уровни коррекции, далее уровни расширения.

Доджи от уровня 0.618, цена прошла до нижнего уровня коррекции фибоначчи, он же уровень сопротивления. Теперь тянем сетку расширения.

И вот что происходит:

• Цена столкнулась с поддержкой 0.382.
• Уровень 0.500 сначала отработал как поддержка и затем как сопротивление.
• Уровень 0.618 тоже был цене весьма интересен. Именно на нем цена задержалась перед движением вниз.

На этих примерах становится понятно, что уровни расширения фибоначчи являются логическим продолжением уровней коррекции и нередко (хотя и не всегда) формируют временные уровни поддержки и сопротивления.

Помните, что гарантированного способа определить, когда уровень фибоначчи отработает как сопротивление или поддержка нет. Однако, применяя все приемы технического анализа, которые мы уже изучили, вы существенно расширяете свои возможности по определению таких вот ситуаций.

Поэтому, уровни расширения и коррекции фибоначчи следует расценивать как вспомогательный, полезный в ряде случаев инструмент. Но не ждите, что цена будет там прыгать, как мячик. Сами понимаете, тогда и ваша бабушка могла бы торговать.

Уровни фибоначчи — зона вашего интереса. Если у этих уровней формируются какие-то свечные комбинации, если осцилляторы или другие инструменты показывают что-то любопытное — самое время насторожиться.

Использование уровней Фибоначчи

Фибоначчи — это технический инструмент, по сути, автоматического построения уровней поддержки и сопротивления. Их нужно дополнять:

• стандартными линиями поддержки и сопротивления;
• линиями тренда;
• японскими свечами;
• вспомогательными индикаторами.

И тогда они станут неплохим помощником в вашей работе. Именно так и создается торговая стратегия, на базе комбинируемых инструментов и изучения их особенностей в разных рыночных условиях.

Три самых важных уровня коррекции фибоначчи, это:

• 0.382 (38.2%)
• 0.5 (50.0%)
• 0.618 (61.8%)

Все остальные уровни, скажем, 0.236 или 0.764 являются вспомогательными.

А это важные уровни расширения:

• 1.00 (100%)
• 1.382 (138.2%)
• 1.618 (161.8%)

Использовать Фибоначчи нетрудно. Берутся свинги (верхний и нижний), как максимальные и минимальные значения цены. От них протягивается сетка, а ее линии используются как намеки на уровни поддержки и сопротивления.

Применять ли Фибоначчи в вашей работе — решать вам. Лично я привык чертить уровни руками, от зон, что выбираю сам. Но при этом вполне понимаю тех, кто использует такие дополнительные инструменты для обнаружения иных зон.

Как мы помним по концепции самоисполняющегося пророчества, чем больше трейдеров используют определенный инструмент, тем большую значимость они имеют. А Фибоначчи — очень популярный инструмент, что нередко проскакивает и на графиках профессиональных банковских трейдеров. Так что это пророчество, что сбывается достаточно часто.

Фибоначчи - последовательность чисел - азбука трейдинга

Леонардо Пизанский, он же Фибоначчи и его уникальная, в своём роде, последовательность чисел, так же как и понятия «золотого сечения», «спираль Фибоначчи» или «число Бога», имеет непосредственное отношение к трейдингу, как к живой среде. На основе последовательности чисел трейдеры выстраивают уровни коррекции, расширения и иные.

Леонардо собственной персоной.

Фибоначчи – кто это?

                Леонардо Пизанский, больше известен по прозвищу Фибоначчи. Один из первых крупных математиков в средневековой Европе. Изучал искусство счёта в Алжире, Индии, Византии, Египте и ещё во многих странах Евразии и Африки. Его посмертный статус провозглашается как: «Пропагандист десятичной системы счисления и использования арабских цифр». Но в первую очередь, в нашем времени Фибоначчи запомнился нам как искусный математик. Сам он родился в Италии, в Пизанской республике и прожил 80 лет. Умер на родине, не оставив о своей биографии абсолютно ничего (все даты лишь предположения историков), за исключением отрывка второго абзаца книги «Абака». Даже портрет, знаменитого средневекового математика. Это лишь примерные наброски со слов историков.

Последовательность чисел Фибоначчи

                Дак какое же отношение Фибоначчи имеет применимо к трейдингу? Наберитесь терпения, дальше самое важное и интересное. Существует выражение, что математика «Царица всех наук». В ней присутствуют темы, с методами вычисления которых, можно раскрыть завесу тайн мировоздания. В мире есть закономерности и явления, которые, как не странно, можно объяснить  на языке математики.

                Главным  важнейшим трудом Фибоначчи, дошедших до наших дней, является последовательность чисел, при котором сумма следующего числа, получается путём сложением двух предыдущих чисел. В письменном виде это выглядит так:

0,1,1,2,3,5,8,13,21,34,55,89,144,…

0+1=1+1=2+1=3+2=5+3=8+5=13+8=21+13=34+21=55+34=89+55=144…

                Данная последовательность хорошо прослеживается в задачке от «Фибоначчи»: Есть два кролика, самец и самка. Условия таковы, что каждый месяц у них появляется на свет потомство, тоже самка и самец. На следующий месяц у этой пары появляется ещё одна пара кроликов. Теперь у нас получилось три пары кроликов. На следующий месяц, путём спаривания между собой в парах, у нас уже 5 пар кроликов. Задача состоит в том, чтобы вычислить, сколько будет кроликов, спустя 1 год. Ответ не так уж и сложен, даже без применения каких либо формул. Достаточно прибегнуть к числовой последовательности Фибоначчи, где одна единица любой цифры будет один кролик. А каждое сложение. Это будет прошествие одного месяца. На выходе мы получим 377 кроликов, если начать счисление от 1+1 (кролик + кролик).

«Золотое сечение» (1,618)

                Золотое сечение это пропорциональное соотношение чисел, при использовании которого в любой сфере жизнедеятельности, проявляется структуризация и гармония. Но всё же, давайте не будем употреблять заучных слов и рассмотрим это явление простым языком. Для простоты восприятия, возьмём любое число из последовательности чисел Фибоначчи. Например, 13. Чтобы нам обнаружить число «золотого сечения», нам необходимо это число разделить на предыдущее в этом же ряду, то есть на 8. В ответе мы получим десятичную дробь 1,625. То есть это не цельное, не круглое число близкое к «золотому сечению».

1,625

Но если мы разделим 144 на 89, то мы получим цифру 1,6179775. Заметили разницу? Во втором примере итоговая цифра изменилась в меньшую сторону. Забегая вперёд, скажу, что чем выше мы будем брать число из последовательности чисел Фибоначчи, тем скорее и ближе будет стремиться итоговая цифра к значению 1,618 (не исключено отклонение как в плюс, так и в минус). К примеру, возьмём далёкое число 10 946 и разделим из этого ряда на предыдущее число 6 765. По итогу получим почти идеальную десятичную дробь 1,6180339. Попрошу вас взять в руки калькулятор и проверить данный пример.

Золотое сечение и трейдинг.

                Но какое же отношение, десятичная дробь 1,618 имеет к трейдингу? Потерпите немного, ведь не знание источников информации приводит к неверным интерпретациям будущих ситуаций на рынке. Понимаете, финансовый рынок, это живая среда. Это мы с вами. Для ясного, ну или примерного представления, приведу пример: Как известно из научных источников, насекомые, в частности пчёлы или муравьи, имеют один, общий инстинктивный «разум». И при строительстве своего муравейника, они не общаются, не обсуждают размер будущего дома, и не собираются вместе на обед. Но почему тогда у них получаются их логова в идеальном для них состоянии и в правильно расположенном месте? Да к тому же с меньшими входами/выходами со стороны севера? Всё потому же, что это инстинкт от природы ОДИН на всех. Ровно поэтому же и всемирный коллектив на FOREX, действует «сообща», «инстинктивным» разумом. Совершая всё те же ошибки, отдавая прибыль и преимущество единицам.

Простейший пример

                Теперь, зная точное (округлённое) число «золотого сечения». Мы с вами можем рассчитать практически любое соотношение. Снова забегая вперёд, оговорюсь; современный человеческий мозг, до сих пор не хочет воспринимать «идеальные» пропорции, как в природе, так и в архитектуре.

                Так в простейший пример можно привести «золотой прямоугольник». То есть прямоугольник с идеальным соотношением сторон. Ширина 754. Высота 466. При делении ширины на высоту, получим десятичную дробь «золотого сечения» 1,6180257. Я по праву не знаю (но догадываюсь) почему данное соотношение сторон не используется на экранах, при выпуске телевизоров или других гаджетов. Но всё же, некоторые устройства имеют приблизительную пропорцию сторон. Я же ссылаюсь на то, что современный человек ещё не пришёл к полной гармонии с «внутренней» природой.

Спираль Фибоначчи

                Весь наш мир в изобилие элементами «золотого сечения». Просто люди, которые далеки от этой темы, не в состоянии этого узреть. Сплошь и рядом прослеживается пропорция 1,618. Одним из важнейших элементов «золотого сечения» является спираль Фибоначчи. И вот те, кто разобрался с этой темой, и прочувствовали всю красоту и гармонию данного явления, несомненно, захотят построить спираль Фибоначчи собственными руками. Для этого нам потребуется циркуль обыкновенный и лист в клеточку. Обязательно в клеточку для того, чтобы можно было чертить аккуратные, правильные квадраты. Начать построение спирали нужно с двух нарисованных одинаковых квадратов, размером в одну клеточку, каждый. Начало спирали соединяет два противоположных угла этих квадратиков, лежащих на одной плоскости. Теперь важное условие; следующий квадрат, который соединяет два предыдущих, должен иметь стороны содержащие количество клеточек в сумме полученные путём сложения количеством клеток двух предыдущих квадратов. И каждый раз спираль (дуга) чертится на противоположный угол по диагонали. Да ребят, просто читая, я бы и сам запутался, для этого я и привёл ниже скриншот.

Спираль и ряд чисел Фибоначчи в природе

                Первозданный вид нашей вселенной, я бы даже сказал, нашего бытия, представлял собой абсолютный хаос. Частицы газа и пыли после «большого взрыва», с течением времени сформировали нашу планету. Но даже и с появлением тверди логичность структуризации не прослеживалась. Лишь спустя много миллионов лет, наша природа  преобразилась, и земля приобрела порядок. Все её царства – животные, растения, грибы (как отдельное царство), насекомые и человек, имеют отдельные элементы спирали Фибоначчи. Список можно продолжать: Вихри, спирали галактик, направления движения орбит планет и их естественных спутников, гребни цунами, спирали ДНК, ушная раковина человека, отпечатки пальцев, а так же молнии (последние имеют и элементы фрактала). Про ДНК же стоит поправиться, что в большей степени в ней присутствует последовательность чисел Фибоначчи, чем сама спираль. Скажу больше; спирали имеются не только у статических природных объектов, но и природных явлений, таких как завихрения, от взмаха крыльев стрекозы (кстати, единственное природное существо, которое имеет способность летать задом наперёд). Это так, к слову, дабы вы не соскучились. А так же, музыкальные такты, паузы, расположение октав, относительно их интервальному тону. Временные спирали, по которым происходят те или иные события. Так же временные периоды тесно связаны и с фрактальной структурой. Вобщем говоря, наш природный мир полностью и целиком приобрёл безграничную красоту и гармонию.

Последовательность ряда чисел Фибоначчи, «золотое сечение» и Спираль Фибоначчи в архитектуре

                Человек, как разумный Хомо сапиенс, тоже стремится к красоте, удобству, гармонии и оптимизации своих творений. Не правильным будет не признать гениальность архитекторов, воздвигнутых под их проектами сооружений. Которые можно описать с помощью математики. В частности все их элементы демонстрируют  ряд чисел Фибоначчи, «золотое сечение», либо Спираль Фибоначчи.

                Вообще в мире и в истории примеров наглядных уйма. Я же приведу в пример самый простенький. Христианский крест. Предположим мы взяли вертикальный элемент креста длинною, ну скажем 1000 см. Значит, горизонтальная перекладина должна быть 618 см. 1000/1,618=618. Далее располагаем её на уровне тоже 618 см. («золотое сечение» по длине стоявой балки), от верхнего края. Условие, что центр крепежа будет на обеих балках на расстоянии 618 см. В итоге мы получаем крест идеальной формы. И вот что удивительно, если вы из выше предложенного примера, правильно наложите спираль Фибоначчи на этот крест, то некоторые элементы совпадут.  Вы сможете это воссоздать сами на листе бумаги в клетку.

Подводя итоги

                На эту тему, примеров можно приводить бесчисленное количество. Но из пройденного материала, думаю, многие читатели поняли, почему ряд чисел Фибоначчи называют «числом Бога». Я же, подводя черту, желаю объяснить начинающим трейдерам, специализирующихся на техническом анализе, зачем так важно знать про последовательность чисел Фибоначчи. Рынок, будь то Forex или любая Биржевая площадка, это всегда живая среда. Инфраструктура похожая на природные явления. Это мы с вами. Коллективные действия, формирующие правила и элементы, так похожие на природные закономерности. К сожалению, в рамках этого материала, мне больше нечем вас удивить. Могу лишь посоветовать поинтересоваться этой темой на каналах в YouTube. Ролики с данным сюжетом, по истине, захватывает дух.

Эта статья – материал из рубрики “Азбука Трейдинга”. Загляните в неё. Там ещё много интересного!

Сложно? “Трейдинг для чайников” – бесплатное обучение рынкам.

Подпишитесь на наш телеграм канал и получите самую лучшую информацию.

Кто такой Фибоначчи? - Мастерок.жж.рф — LiveJournal

Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.

В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.

Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.

Каждое число из ряда Фибоначчи, разделенное на предыдущее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.

Леонардо Пизанский — тот самый создатель числа Фибоначчи

 

Почему число Фибоначчи так часто используется в природе?

Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.

 

Проявление золотого сечения в природе

Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!

Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.

Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением

С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе. Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.

источник: hi-news.ru

Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты

Это копия статьи, находящейся по адресу https://masterokblog.ru/?p=47228.

как можно их использовать в трейдинге?

Вам, вероятно, знакомы уровни Фибоначчи? Независимо от того, используете ли вы их в качестве дополнения к своей торговой стратегии или просто наносите на график для подтверждения ключевых уровней поддержки и сопротивления, они всегда могут оказаться полезны в техническом анализе.

Кто такой Фибоначчи?

Леонардо Боначи (более известный как Фибоначчи) родился около 1170 года и был одним из самых талантливых математиков своего времени.

Он не только разработал последовательность чисел Фибоначчи, с которой знакомы все трейдеры, но также популяризировал арабскую систему счисления в западном мире. Однако его главным достижением считается исследование чисел Фибоначчи.

Леонардо Фибоначчи обнаружил, что простой ряд чисел можно использовать для описания самых разных пропорций в природе: от исследования Вселенной до определения кривизны раковин улиток и структуры семян растений.

Как работает последовательность Фибоначчи?

Большинство трейдеров не понимают, как работает последовательность Фибоначчи. В конце концов, торговые платформы предоставляют нам инструмент расширения Фибоначчи, в котором уже есть встроенные математические функции. Все, что нам нужно сделать, это нажать на кнопку и перетащить расширение Фибоначчи на свой график. Однако давайте попробуем разобраться в его закономерностях.

Последовательность чисел Фибоначчи выглядит следующим образом:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д.

Каждое число в данной последовательности является суммой двух предыдущих чисел:

0 + 1 = 1
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
и т. д.

Что в этом особенного? Каждое число в последовательности примерно в 1,618 раз больше предыдущего числа. Таким образом, хотя все цифры разные, они имеют одну общую закономерность.

Если вы знакомы с уровнями коррекции Фибоначчи, вы знаете, что значение 1.618 или 61,8% чрезвычайно важно. Число 1.618 называется «золотым сечением» или «золотой серединой».

Соотношение 38,2% получается путем деления любого числа в ряду на число, размещенное на две позиции справа:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д.

13 / 34 = 0,382.

Соотношение 23,6% получается делением любого числа в ряду на число, размещенное на три позиции справа:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. Д.

13 / 55 = 0,236.

Таким образом, мы получаем соотношения 61,8%, 38,2% и 23,6%.

Так что же делает эти соотношения такими особенными? Это до сих пор неясно. Данные соотношения играют важную роль как в природе, так и на финансовых рынках. Мы можем использовать расширения Фибоначчи для определения ключевых уровней, на которых цена может развернуться.

Что общего у панциря улитки с графиками? Все правильно, они связаны с числами Фибоначчи. Прибыль, которую вы только что получили от продажи EURUSD на уровне Фибоначчи 61,8%, во многом можно объяснить изучением растений, цветов и даже раковин улитки. Эти уровни, которые мы используем на своих графиках, впервые были изучены в природе. В конце концов, сам Фибоначчи никогда не был трейдером.

Однако следует отметить, что не на всех графиках присутствуют данные закономерности. Вы обнаружите, что некоторые валютные пары больше уважают эти уровни, чем другие.

Боначчи пытался найти числовой порядок для упорядочивания хаоса в окружающем мире. В мире трейдинга его последовательность чисел помогает объяснить закономерности движения цены. В конечном итоге, технический анализ и наши действия как трейдеров зависят от повторяющихся ценовых шаблонов, паттернов и уровней.

Уровни коррекции Фибоначчи в действии

Уровни коррекции Фибоначчи наиболее эффективны при использовании на максимумах и минимумах движения цены.

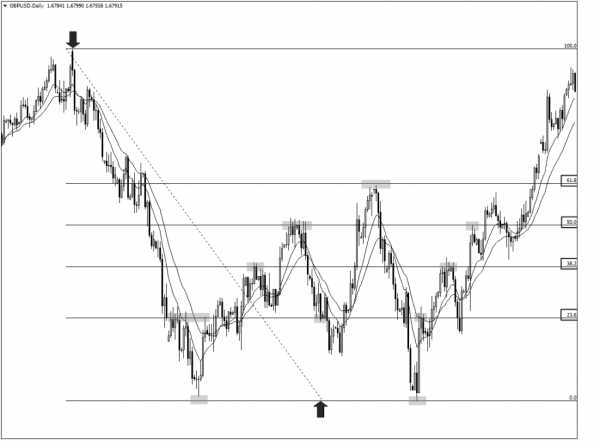
Максимум цены используется в качестве начальной точки расширения, а минимум – в качестве конечной точки. Как вы заметили, цена постоянно учитывает уровни Фибоначчи.

В дополнение к коэффициентам, которые мы обсуждали выше, многие трейдеры также используют уровень 50%. Хотя это и не соотношение Фибоначчи, у рынка есть тенденция продолжать движение в определенном направлении после 50% отката. Поэтому уровень 50% был добавлен к большинству инструментов расширения Фибоначчи.

Как использовать уровни Фибоначчи в сочетании с горизонтальными уровнями и сигналами прайс экшен?

Распространенные вопросы среди трейдеров: действительно ли работают уровни расширения Фибоначчи и есть ли от них польза? Я без сомнения могу сказать, что они работают и могут быть полезны, но только при правильном использовании. Рассмотрим, как можно использовать уровни Фибоначчи в сочетании с прайс экшен.

На графике ниже мы используем основной минимум движения цены в качестве начальной точки и основной максимум в качестве конечной точки. Эти две точки являются наиболее заметными на графике:

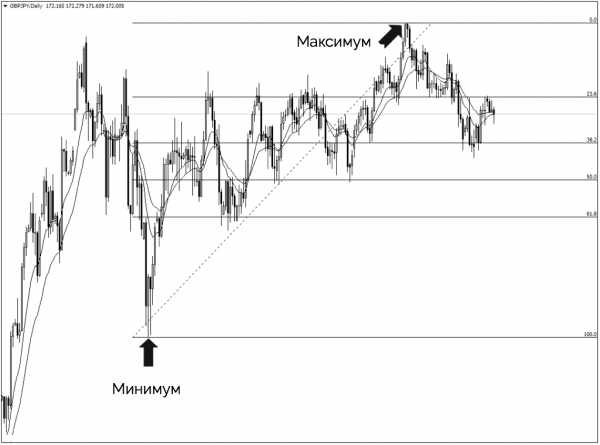
Теперь становится очевидно, что на графике есть несколько четко определенных уровней.

Обратите внимание, как уровни Фибоначчи 38,2, 50 и 61,8 совпадают с горизонтальными уровнями поддержки и сопротивления, от которых происходил отскок цены. Это дает нам дополнительную уверенность, что на этих уровнях рынок может развернуться.

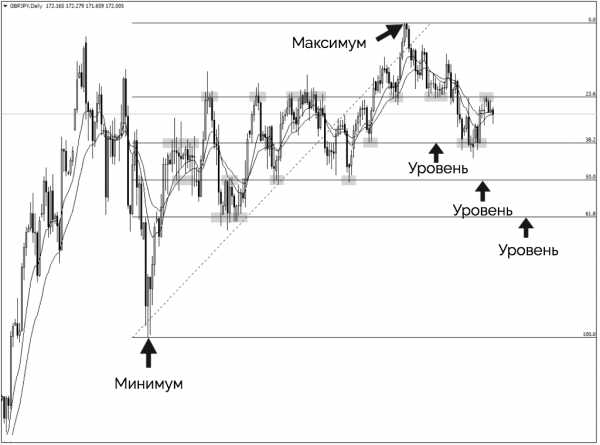
Никогда не следует использовать уровни Фибоначчи сами по себе. Как и все остальное в техническом анализе, уровни Фибоначчи – это лишь еще один структурный фактор, который мы можем добавить в наш набор инструментов для торговли.

Мы можем использовать инструмент Фибоначчи для дополнительного подтверждения движения цены. Воспринимайте его как еще один взгляд на рынок и ориентируйтесь прежде всего на горизонтальные уровни, которые уже должны быть проведены на вашем графике.

На примере ниже мы видим, как рынок продолжает свое движение между двумя уровнями:

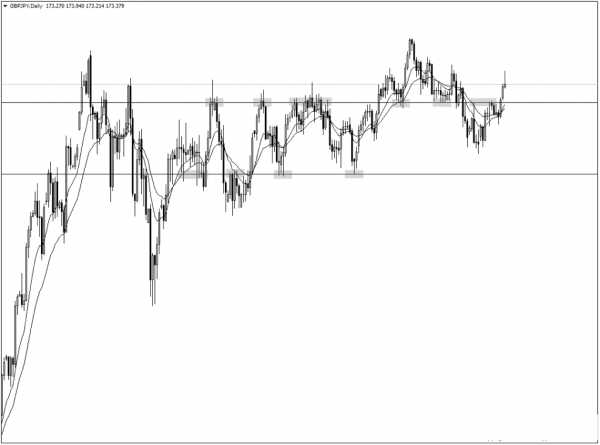
Теперь мы можем использовать инструмент расширения Фибоначчи, чтобы увидеть, совпадают ли еще какие-либо уровни:

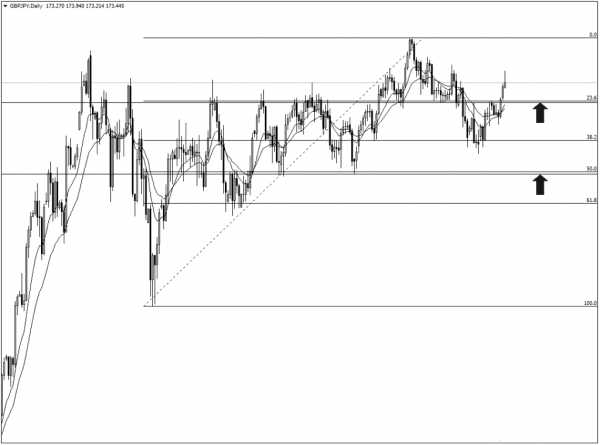
Как только мы нарисуем уровни Фибоначчи, сразу становится очевидным, что уровни 23,6 и 50 идеально совпадают с нашими горизонтальными уровнями, которые мы определили ранее. Это дает нам большую уверенность в том, что любое движение цены к этим уровням должно привести к увеличению спроса и с большей вероятностью вызовет определенную реакцию рынка.

Что делать, если уровни Фибоначчи не совпадают с уровнями поддержки и сопротивления? Они также могут играть определенную роль, просто они не будут ключевыми уровнями, на которые следует обращать внимание в первую очередь.

Как можно видеть на графике выше, уровни 38,2 и 61,8 стали причиной отскока цены в последующее время.

Вы также можете использовать инструмент расширения Фибоначчи, чтобы найти ключевые уровни, которые вы, возможно, пропустили. Ключ к эффективному использованию инструмента Фибоначчи – это использовать его только на старших таймфреймах. То есть дневных или недельных графиках.

Используя недельный график, мы ясно видим, что уровень 148 является ключевым горизонтальным уровнем:

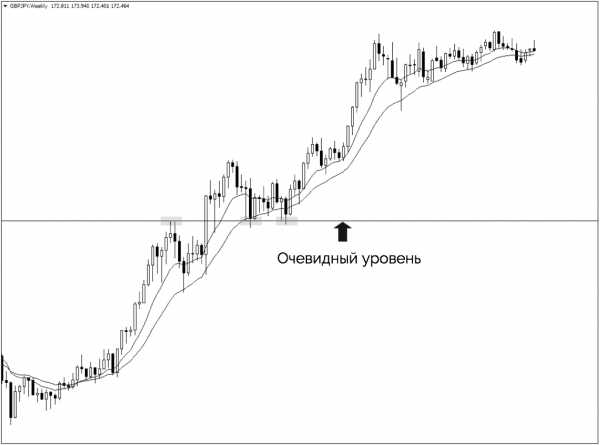
Теперь давайте перетащим инструмент Фибоначчи с минимума на максимум, чтобы увидеть, есть ли еще и другие уровни:

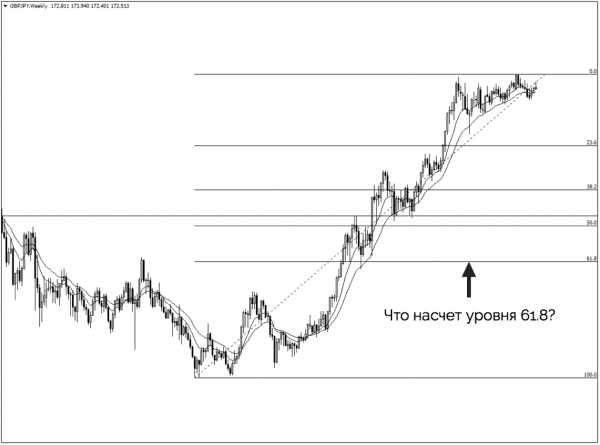
Первое, что мы должны заметить, это то, что уровень отката 50% не соответствует заранее определенному нами уровню. Но это нормально! Помните, что очевидный горизонтальные уровень всегда будет важнее уровня Фибоначчи.

Пj смотрим на уровни 23.6, 38.2 и 61.8. С первого взгляда можно увидеть, что уровень 61,8 пытается нам что-то сказать. Нарисуем горизонтальный уровень над уровнем коррекции Фибоначчи 61,8 и посмотрим:

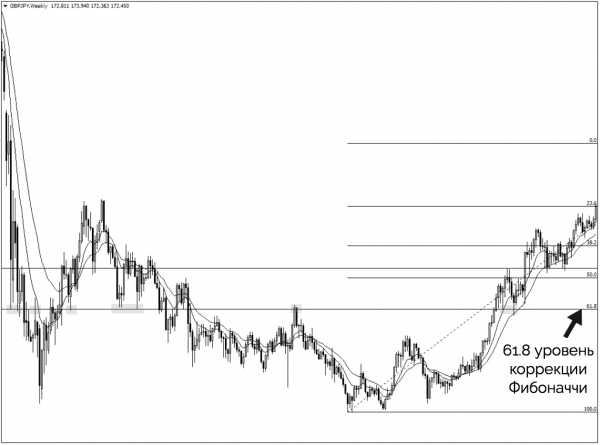
Теперь становится очевидно, что это ключевой горизонтальный уровень, на который мы должны обратить внимание. График выше показывает, как текущий уровень коррекции Фибоначчи 61,8 повлиял на движение рынка за последние несколько лет.

Теперь пришло время найти сигнал прайс экшен на уровне слияния.

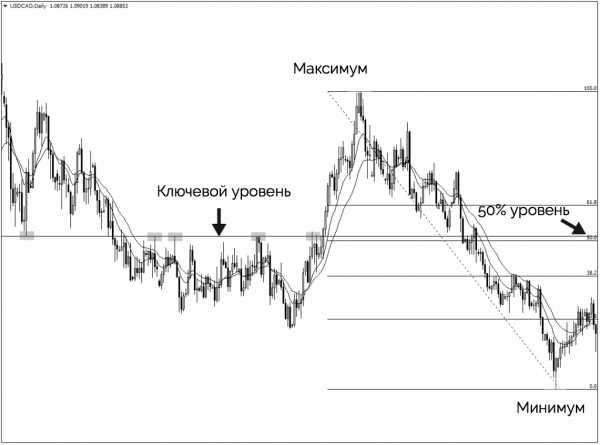
Совершенно очевидно, что уровень 50% идеально соответствует недавним максимумам движения цены. Поэтому мы отмечаем данный уровень на нашем графике и наблюдаем за ценой, если она вернется в эту область.

Через два месяца рынок снова возвращается к области сопротивления 1.005 и формируется медвежий пин бар:

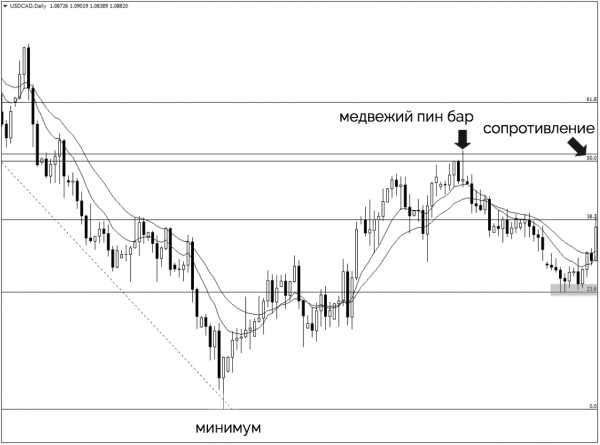
Обратите внимание, что рынок снова находит поддержку на уровне Фибоначчи 23,6.

Это прекрасный пример того, как мы можем получить прибыль от использования уровней коррекции Фибоначчи в сочетании с с прайс экшен.

Во многих отношениях причина, по которой уровни Фибоначчи настолько эффективны, до сих пор остается загадкой. Однако в техническом анализе нам не обязательно нужно знать, почему что-то работает. Мы можем просто использовать этот инструмент и получать выгоду.

Не забывайте, что уровни коррекции Фибоначчи работают и могут быть чрезвычайно полезными только в сочетании с другими торговыми стратегиями, подобными прайс экшен.

Эффективность этой комбинации может быть объяснена тем фактором, что данные инструменты широко используются многими трейдерами, что вызывает определенную реакцию рынка.

Как определять разворотные точки рынка с помощью уровней Фибоначчи?

Большинство трейдеров наносят уровни Фибоначчи на 1-часовой или 4-часовой график, который охватывает несколько дней или несколько недель. Кроме того, эти же трейдеры используют расширение Фибоначчи только после того, как цена совершает откат. Однако поступая подобным образом, они упускают из виду общий рыночный контекст.

К примеру, вы наносите уровни коррекции Фибоначчи на дневной график NZDUSD во время восходящего тренда и обнаруживаете совпадение с ценой на нескольких уровнях. Помните, что мы не используем инструмент Фибоначчи для поиска ключевых уровней, а только для их дополнительного подтверждения.

Наш график будет выглядеть примерно так:

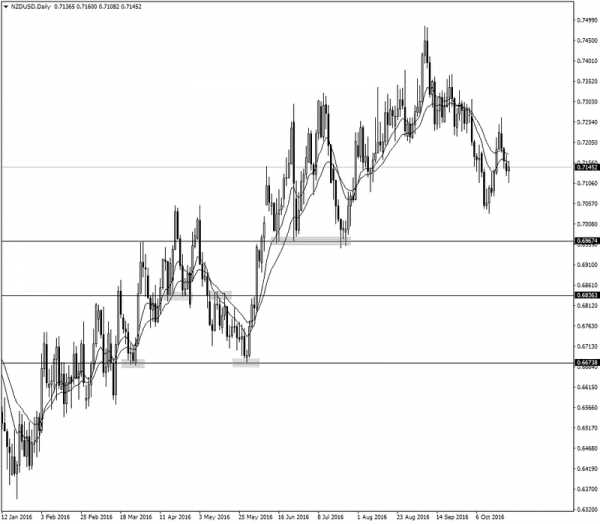
Затем мы используем расширение Фибоначчи и перетаскиваем уровни с минимума на последний максимум:

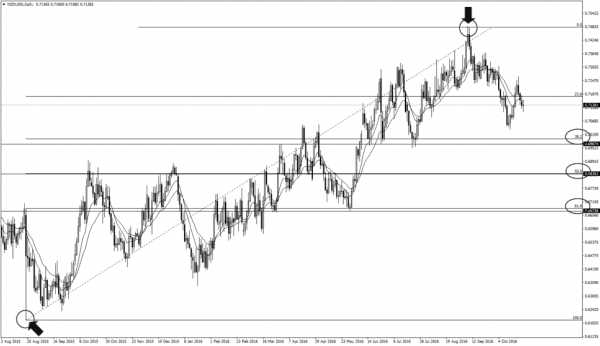
Все три уровня совпадают с числами Фибоначчи 61,8%, 50% и 38,2%.

Большинство трейдеров рассматривают потенциальные возможности для покупки на одном из уровней слияния. В конце концов, рынок находится в восходящем тренде.

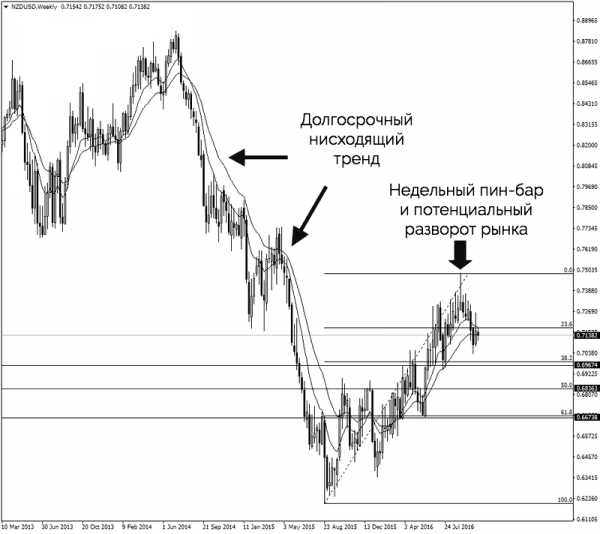
Однако далее мы видим медвежий флаг, где уровни Фибоначчи совпадают с заранее определенными областями поддержки. Если рынок вырастет выше текущего максимума, уровни Фибоначчи не будут совпадать с нашими уровнями поддержки. По сути, мы используем общую картину рынка в сочетании инструментом Фибоначчи для определения основных разворотных точек.

Помните, что технический анализ действителен только в общем рыночном контексте. То, что выглядит как возможность для покупки, вполне может оказаться признаком слабости в условиях долговременного нисходящего тренда.

Как находить вершины рынка с помощью уровней Фибоначчи?

Максимумы и минимумы движения цены не так часто встречаются на графиках.

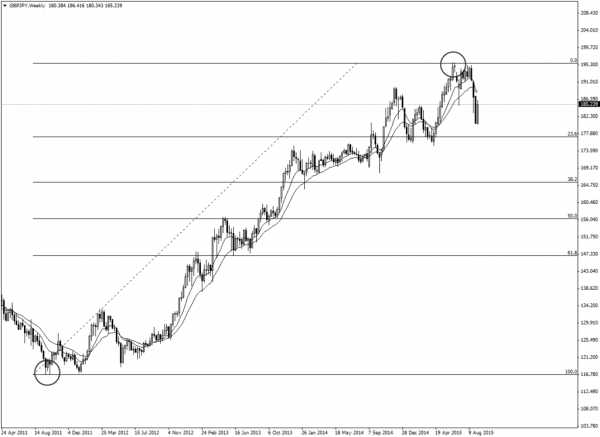
Недельный график GBPJPY показывает простоту моего метода. Я просто перетащил инструмент расширения Фибоначчи с минимума колебания до недавнего максимума. Давайте внимательнее посмотрим, что здесь происходит.

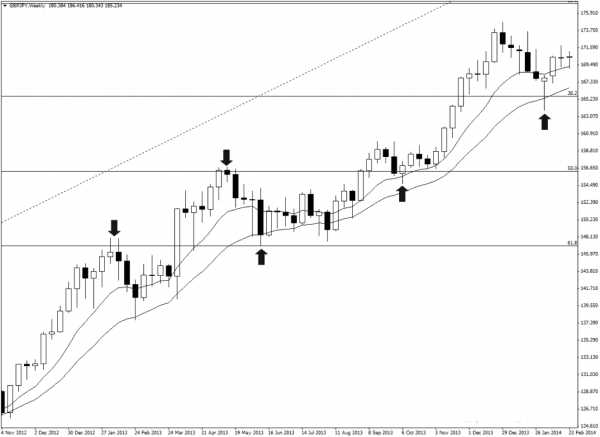
Обратите внимание, как каждый уровень расширения Фибоначчи совпадает с максимумами или минимумами движения цены. Это отчетливый сигнал того, что рынок достиг своей вершины и, вероятно, вскоре произойдет его разворот.

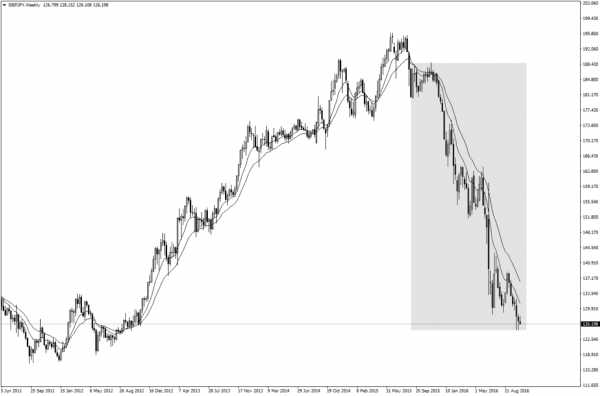
Вот еще один пример:

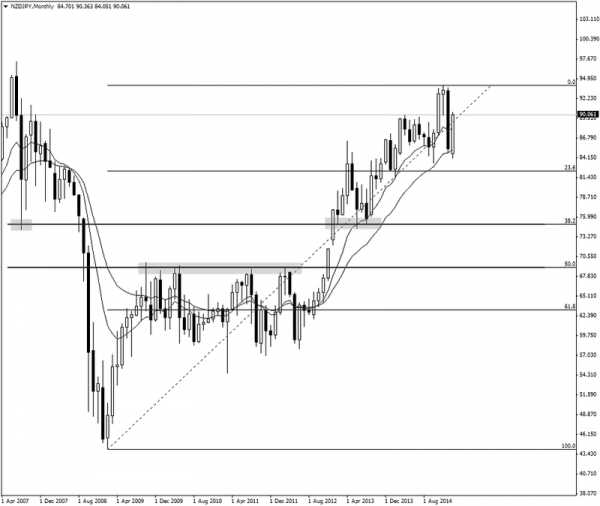
Обратите внимание, как уровни коррекции Фибоначчи 38,2% и 50% идеально совпадают с важными горизонтальными уровнями поддержки и сопротивления. Это вновь не простое совпадение. Подобная закономерность говорит о достижении рынком своей вершины.

Вот, что произошло далее:

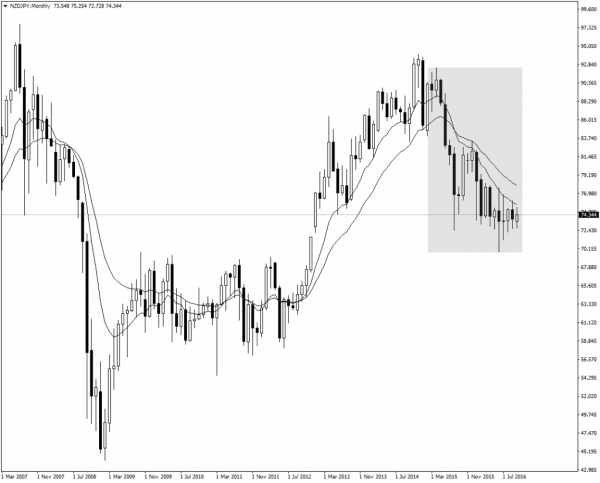
Цена упала на 1600 пунктов.

Как я узнал, что цена достигла своего многолетнего максимума? Так как два уровня коррекции Фибоначчи идеально совпали с максимумами и минимумами движения цены, это было очевидным намеком на то, что на рынке намечается серьезный разворот.

Уровни Фибоначчи и повышенная волатильности

Технический анализ – это смесь искусства и науки. И хотя мы точно не знаем, почему он работает, одна вещь очевидна: он опирается на восприятия рынка большинством трейдеров. Уровень или паттерн, который очевидны для одного трейдера, также являются очевидными и для многих других трейдеров.

Волатильность часто отрицательно влияет на технический анализ, в том числе при использовании инструмента расширения Фибоначчи.

Что происходит, когда уровень или паттерн видны только небольшому количество трейдеров, которые торгуют на одном и том же брокере?

Рассмотрим пример. Какой из двух максимумов на графике ниже следует использовать в качестве точки для определения ключевых уровней Фибоначчи?

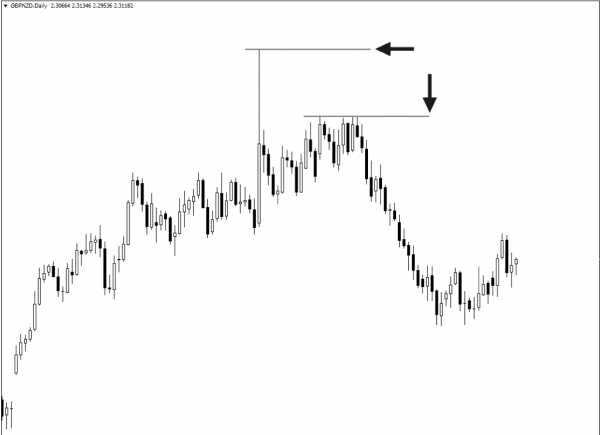
В нормальных обстоятельствах мы должны были использовать последний ценовый максимум. Однако данный максимум будет отличаться у разных брокеров. Обратите внимание на несоответствие уровней Фибоначчи, которые возникли из-за разного размера тени сверхволатильной свечи:

Увеличение волатильности привело к формированию трех разных максимумов для одной и той же валютной пары у разных брокеров.

Помните, что рынок форекс децентрализован, и это означает, что существует большая вероятность разных значений цены среди разных поставщиков ликвидности, особенно если волатильность сильно возрастает. Это представляет огромную проблему для трейдера, который пытается определить истинный максимум колебания, чтобы использовать инструмент расширения Фибоначчи.

Представьте, что будет, если три трейдера попытаются нарисовать уровни Фибоначчи:

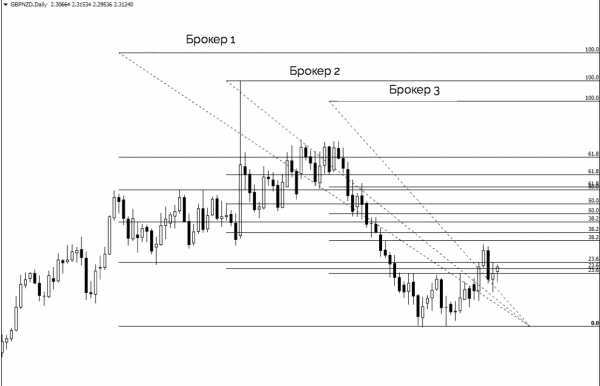
Мы можем сделать вывод, что расширение Фибоначчи работает только в определенных рыночных условиях, когда на рынке нет подобных всплесков волатильности. Если вы будете использовать его в периоды повышенной волатильности, как на графике выше, инструмент окажется совершенно бесполезным, поскольку может привести к ложной картине при прорисовке ключевых уровней.

Что вы можете сделать, столкнувшись с подобными всплесками волатильности?

Первое и самое очевидное: ничего не делать. Помните, что ваша главная работа в качестве трейдера заключается в защите вашего торгового капитала. К тому же у вас всегда есть десятки других валютных пар для торговли. Поэтому независимо от того, насколько хорошо может выглядеть торговая установка, полезно знать, что она, скорее всего, не единственная.

Следующий вариант заключается в поиске соответствий уровней расширения Фибоначчи и горизонтальных уровней на графике. Это даст нам дополнительное подтверждение, имеют ли данные уровни какую-либо силу.

Избегайте ложных сигналов

Самый лучший способ избежать ложных сигналов – это всегда использовать уровни коррекции Фибоначии на старших таймфреймах.

Я предпочитаю использовать недельные или месячные графики для определения возможного разворота рынка. Чем больше будет расстояние между максимумами и минимумами, тем лучше. Старайтесь охватить расстояние хотя бы в несколько лет.

Наконец, самый лучший способ избежать ложных сигналов – это никогда не полагаться на одну торговую стратегию. Не существует лучшего способа использовать уровни Фибоначчи. Всегда спрашивайте себя, подходит ли данный метод торговли под ваш стиль трейдинга и вашу индивидуальность?

Феномен 50% отката

Почему у меня такая сильная любовь к уровню 50%? Уберем все уровни Фибоначчи и оставим лишь тот, который имеет 50% отметку:

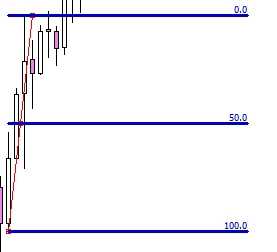
Три линии, всё чётко и ясно. В тренде это самый сильный уровень, из которого можно выжать максимум прибыли с наилучшими точками входа.

Почему не другие уровни? Для меня достаточно одной причины: все остальные уровни не так ненадёжны, их часто пробивают, и стоп-лосс приходится выставлять больше, чем предполагалось.

Для начала, давайте нанесём этот уровень на график, например на 4-х часовом таймфрейме для анализа возьмём одну свечу.

Далее переключимся на часовой таймфрейм и посмотрим, что там произошло.

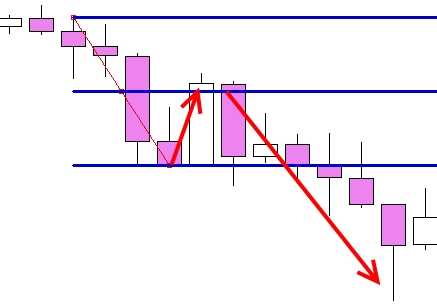
Как мы можем видеть, цена поднялась ровно к 50% и начала своё снижение, при этом принося нам прибыль.

Для стоп-лосса я советую использовать уровень 61.8%, так как пробой этого уровня является сильным сигналом того, что тренд развернулся.

Отскок от 50% уровня Фибоначчи с пин баром

Трейдеры, создающие сильные движения, используют в своей торговле 50.0% уровень Фибоначчи.

Не составит никакого труда, чтобы нанести этот уровень на график. Единственное, что вам нужно знать, это те места, где движение начинается, а где завершается. Самый пик или минимум цены – это та точка, где движение начинается, то место, из которого мы должны начать растягивать уровни Фибоначчи, до следующей остановки движения цены. Для более понятной картины посмотрите на пример расположенный ниже.

На графике мы следим за тем, как именно применять инструменты Фибоначчи для того, чтобы найти 50.0% уровень сопротивления валютной пары EUR/USD:

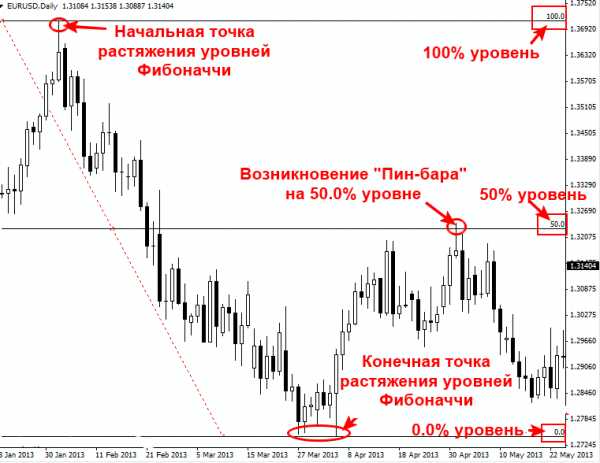
Как торговать от 50% уровня расширения? Когда вы получили сигнал прайс экшен, вы растягиваете уровни Фибоначчи и смотрите, совпадает ли этот сигнал с 50.0% расширением, если да, тогда это отличная точка для входа в рынок. Если в этой точке находится горизонтальный уровень поддержки или сопротивления, можно вас поздравить, вы, можно сказать, «нарвались» на идеальную сделку.

Процесс торговли от 50.0% уровня очень прост:

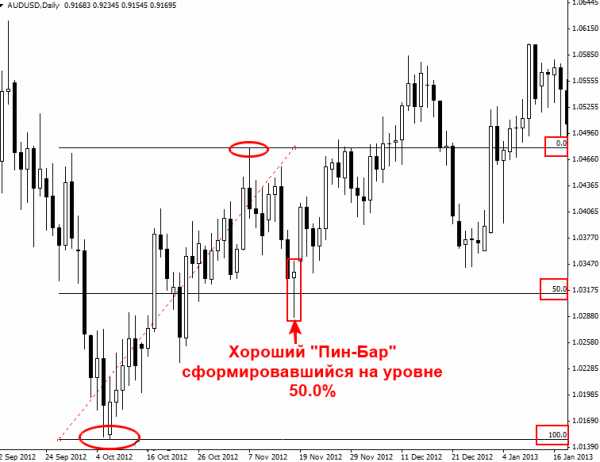
Из примера выше, мы видим образовавшийся пин бар на 50.0% уровне Фибоначчи, далее цена продолжила свой рост, при этом моментум находился на нашей стороне, что послужило дополнительным подтверждением на вход в рынок.

Очень часто, отскок от этого уровня может привести к большим движениям цены на дневных временных интервалах, и изучение этого инструмента может расширить ваш арсенал для торговли.

После обнаружения потенциальной точки входа в рынок, постарайтесь определить факторы, которые могут помешать определенному вами движению, а позже найдите те плюсы, которые будут играть на вашей стороне. Не следует входить в рынок каждый раз, когда вы видите подходящую торговую возможность. Задайте определенные вопросы именно об этой точке входа и постарайтесь найти ответы на них. Запомните: лучше всего играть на стороне общего направления движения.

На следующем графике расположенном ниже, мы видим, что сигнал прайс экшен и уровня 50.0% появились в один момент, это является отличным сигналом для открытия ордера. Как мы можем заметить, последующее движение цены было агрессивным и направлено вверх. Позже, оно создало новые максимумы и принесло нам соответствующую прибыль.

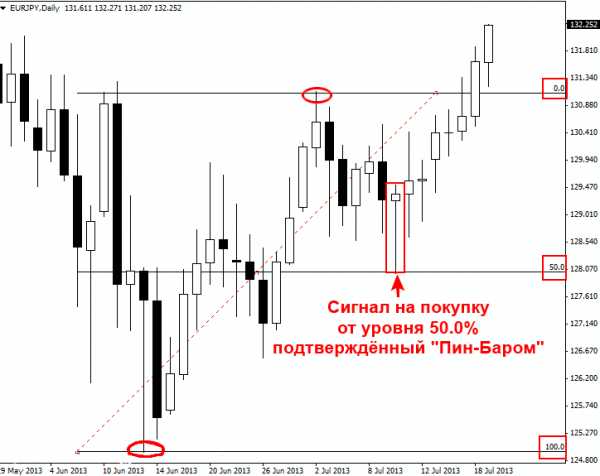
реализация и сравнение / Habr

Введение

Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.

Код предназначен для Python 3, хотя должен идти и на Python 2.

Для начала – напомню определение:

F_n= F_n-1+ F_n-2

и F₁= F₂=1.

Замкнутая формула

Пропустим детали, но желающие могут ознакомиться с выводом формулы. Идея в том, чтобы предположить, что есть некий x, для которого F_n = xⁿ, а затем найти x.

что означает

сокращаем x^n-2

Решаем квадратное уравнение:

Откуда и растёт «золотое сечение» ϕ=(1+√5)/2. Подставив исходные значения и проделав ещё вычисления, мы получаем:

что и используем для вычисления F_n.

from __future__ import division import math def fib(n): SQRT5 = math.sqrt(5) PHI = (SQRT5 + 1) / 2 return int(PHI ** n / SQRT5 + 0.5) 

Хорошее:
Быстро и просто для малых n
Плохое:
Требуются операции с плавающей запятой. Для больших n потребуется большая точность.
Злое:
Использование комплексных чисел для вычисления F_n красиво с математической точки зрения, но уродливо — с компьютерной.

Рекурсия

Самое очевидное решение, которое вы уже много раз видели – скорее всего, в качестве примера того, что такое рекурсия. Повторю его ещё раз, для полноты. В Python её можно записать в одну строку:

fib = lambda n: fib(n - 1) + fib(n - 2) if n > 2 else 1 

Хорошее:
Очень простая реализация, повторяющая математическое определение
Плохое:
Экспоненциальное время выполнения. Для больших n очень медленно
Злое:
Переполнение стека

Запоминание

У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fib(n), то подсчитываются fib(n-1) и fib(n-2). Но когда считается fib(n-1), она снова независимо подсчитает fib(n-2) – то есть, fib(n-2) подсчитается дважды. Если продолжить рассуждения, будет видно, что fib(n-3) будет подсчитана трижды, и т.д. Слишком много пересечений.

Поэтому надо просто запоминать результаты, чтобы не подсчитывать их снова. Время и память у этого решения расходуются линейным образом. В решении я использую словарь, но можно было бы использовать и простой массив.

M = {0: 0, 1: 1} def fib(n): if n in M: return M[n] M[n] = fib(n - 1) + fib(n - 2) return M[n] 

(В Python это можно также сделать при помощи декоратора, functools.lru_cache.)

Хорошее:
Просто превратить рекурсию в решение с запоминанием. Превращает экспоненциальное время выполнение в линейное, для чего тратит больше памяти.
Плохое:
Тратит много памяти
Злое:
Возможно переполнение стека, как и у рекурсии

Динамическое программирование

После решения с запоминанием становится понятно, что нам нужны не все предыдущие результаты, а только два последних. Кроме этого, вместо того, чтобы начинать с fib(n) и идти назад, можно начать с fib(0) и идти вперёд. У следующего кода линейное время выполнение, а использование памяти – фиксированное. На практике скорость решения будет ещё выше, поскольку тут отсутствуют рекурсивные вызовы функций и связанная с этим работа. И код выглядит проще.

Это решение часто приводится в качестве примера динамического программирования.

def fib(n): a = 0 b = 1 for __ in range(n): a, b = b, a + b return a 

Хорошее:
Быстро работает для малых n, простой код
Плохое:
Всё ещё линейное время выполнения
Злое:
Да особо ничего.

Матричная алгебра

И, наконец, наименее освещаемое, но наиболее правильное решение, грамотно использующее как время, так и память. Его также можно расширить на любую гомогенную линейную последовательность. Идея в использовании матриц. Достаточно просто видеть, что

А обобщение этого говорит о том, что

Два значения для x, полученных нами ранее, из которых одно представляло собою золотое сечение, являются собственными значениями матрицы. Поэтому, ещё одним способом вывода замкнутой формулы является использование матричного уравнения и линейной алгебры.

Так чем же полезна такая формулировка? Тем, что возведение в степень можно произвести за логарифмическое время. Это делается через возведения в квадрат. Суть в том, что

где первое выражение используется для чётных A, второе для нечётных. Осталось только организовать перемножения матриц, и всё готово. Получается следующий код. Я организовал рекурсивную реализацию pow, поскольку её проще понять. Итеративную версию смотрите тут.

def pow(x, n, I, mult): """ Возвращает x в степени n. Предполагает, что I – это единичная матрица, которая перемножается с mult, а n – положительное целое """ if n == 0: return I elif n == 1: return x else: y = pow(x, n // 2, I, mult) y = mult(y, y) if n % 2: y = mult(x, y) return y def identity_matrix(n): """Возвращает единичную матрицу n на n""" r = list(range(n)) return [[1 if i == j else 0 for i in r] for j in r] def matrix_multiply(A, B): BT = list(zip(*B)) return [[sum(a * b for a, b in zip(row_a, col_b)) for col_b in BT] for row_a in A] def fib(n): F = pow([[1, 1], [1, 0]], n, identity_matrix(2), matrix_multiply) return F[0][1] 

Хорошее:
Фиксированный объём памяти, логарифмическое время
Плохое:
Код посложнее
Злое:
Приходится работать с матрицами, хотя они не так уж и плохи

Сравнение быстродействия

Сравнивать стоит только вариант динамического программирования и матрицы. Если сравнивать их по количеству знаков в числе n, то получится, что матричное решение линейно, а решение с динамическим программированием – экспоненциально. Практический пример – вычисление fib(10 ** 6), числа, у которого будет больше двухсот тысяч знаков.

n = 10 ** 6
Вычисляем fib_matrix: у fib(n) всего 208988 цифр, расчёт занял 0.24993 секунд.
Вычисляем fib_dynamic: у fib(n) всего 208988 цифр, расчёт занял 11.83377 секунд.

---

Теоретические замечания

Не напрямую касаясь приведённого выше кода, данное замечание всё-таки имеет определённый интерес. Рассмотрим следующий граф:

Подсчитаем количество путей длины n от A до B. Например, для n = 1 у нас есть один путь, 1. Для n = 2 у нас опять есть один путь, 01. Для n = 3 у нас есть два пути, 001 и 101. Довольно просто можно показать, что количество путей длины n от А до В равно в точности F_n. Записав матрицу смежности для графа, мы получим такую же матрицу, которая была описана выше. Это известный результат из теории графов, что при заданной матрице смежности А, вхождения в Аⁿ — это количество путей длины n в графе (одна из задач, упоминавшихся в фильме «Умница Уилл Хантинг»).

Почему на рёбрах стоят такие обозначения? Оказывается, что при рассмотрении бесконечной последовательности символов на бесконечной в обе стороны последовательности путей на графе, вы получите нечто под названием "подсдвиги конечного типа", представляющее собой тип системы символической динамики. Конкретно этот подсдвиг конечного типа известен, как «сдвиг золотого сечения», и задаётся набором «запрещённых слов» {11}. Иными словами, мы получим бесконечные в обе стороны двоичные последовательности и никакие пары из них не будут смежными. Топологическая энтропия этой динамической системы равна золотому сечению ϕ. Интересно, как это число периодически появляется в разных областях математики.

Что такое Числа Фибоначчи - Узнай Что Такое

Числа Фибоначчи — это последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … Следующее число можно посчитать, сложив два числа перед ним.

Т. е. 0 + 1 = 1; 1 + 1 = 2, 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8; …

Более формальное определение ряда Фибоначчи можно показать следующим равенством:

Более длинный список последовательности чисел Фибоначчи:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811,...

Запомнить его довольно просто: нужно только помнить, что первые два числа — это 0 и 1, и начать складывать. И за этим занятием можно просидеть сутками.

"Золотое число" или "Золотое сечение"

Если разделить два последовательных числа друг на друга (например 55 разделить на 34), всегда получится приблизительно 1,618 (обозначается как Φ = 1,618, читается как "фи", это буква греческого алфавита).

1,618 называется "Золотое число" или "Золотое сечение".

55 / 34 = 1,6176

89 / 55 = 1,61818

377 / 233 = 1,618

Использование золотого сечения для вычисления чисел Фибоначчи

Можно вычислить любое число Фибоначчи, используя золотое сечение следующими способами

Формулой

Например, можно попробовать посчитать для n = 10 (внимание, это будет одиннадцатое число в ряду!)

Получился такой ответ:

Умножением предыдущего числа на золотое сечение

Этот способ работает для чисел выше 1. Можно рассчитать число Фибоначчи, умножив предыдущее число на золотое сечение (1,618), а затем округлив полученный результат.

Например:

13 x 1,618 = 21,034 ≈ 21

55 x 1,618 = 88,99 ≈ 89

377 x 1,618 = 609,986 ≈ 610

Золотая спираль Фибоначчи

Это спираль, которая выглядит следующим образом:

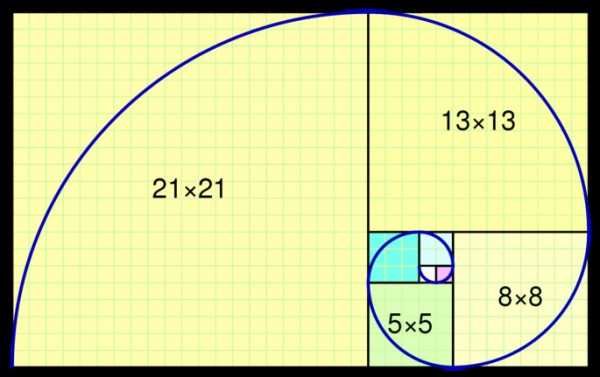Числа Фибоначчи — последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

Как можно видеть на изображении, тут представлен числовой ряд Фибоначчи как спираль. Она начинается в центре с двух квадратов 1x1, за ними следуют квадраты 2x2, 3x3, 5x5 и так далее.

Числа Фибоначчи в природе

Фотография "Алоэ многолистное" (Aloe polyphylla), на фото можно увидеть спираль Фибоначчи в природе. "Спираль ракушки", фотограф Muffett68 Heidi; ещё один пример спирали Фибоначчи в природе.

В этом видео "ЧИСЛА ФИБОНАЧЧИ УДИВИТЕЛЬНАЯ ЗАКОНОМЕРНОСТЬ" ещё больше примеров чисел Фибоначчи в природе и в мире вокруг нас.

Числа Фибоначчи в архитектуре

В строениях древней архитектуры мы зачастую можем ощущать некую гармонию пропорций. И это неслучайно, ведь на протяжении многих веков архитекторы пользуются этим магическим числом золотого сечения. Число 1,618 можно заметить и в творчестве средневековья, и в современных произведениях архитектурного искусства.

Здание SOMISA в Буэнос-Айресе, Аргентина; архитектор Марио Роберто Альварес, окончание строительства 1977 г.

Пример использования золотого числа в древней архитектуре:

Пантеон в Париже

Любопытные факты

Давайте ещё раз посмотрим на последовательность чисел Фибоначчи:

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
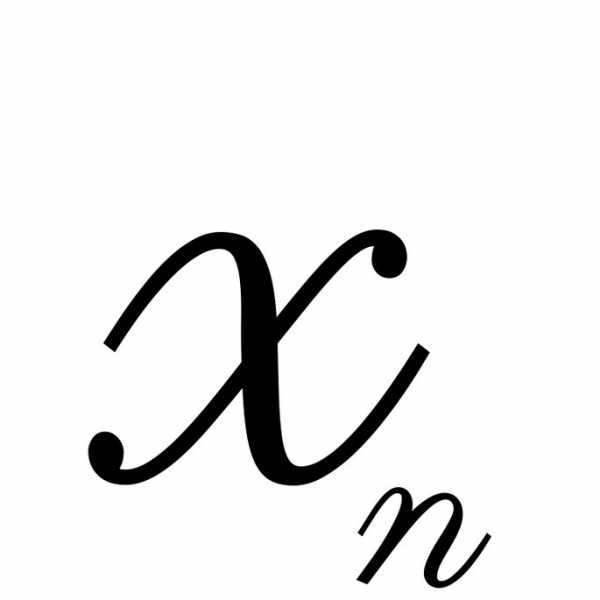	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597

Каждое n-е число кратно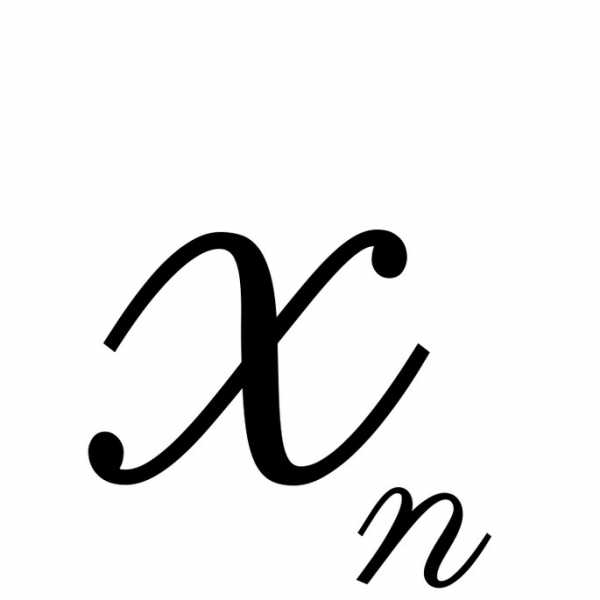

Если внимательно посмотреть на цифры, можно рассмотреть удивительную закономерность:

• посмотрите на 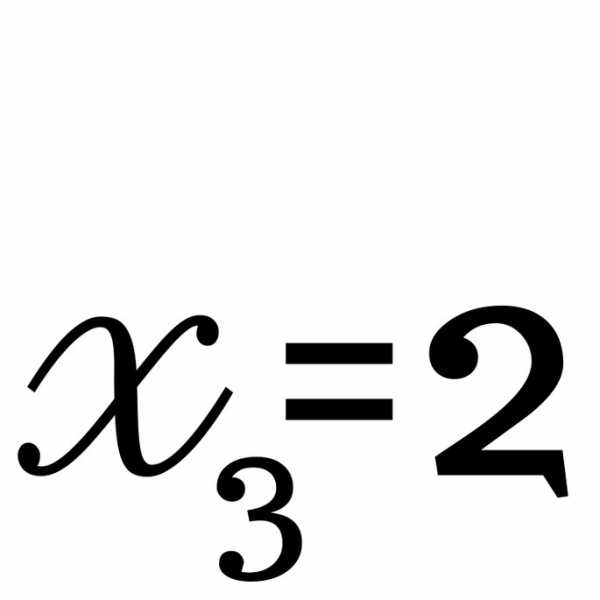, а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый... Каждый третий элемент делится на 2!
• посмотрите на 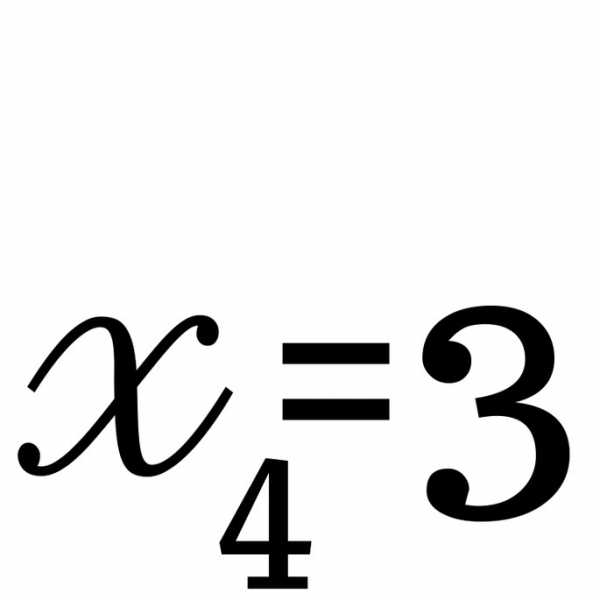, а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый... Каждый четвёртый элемент делится на 3!
• посмотрите на 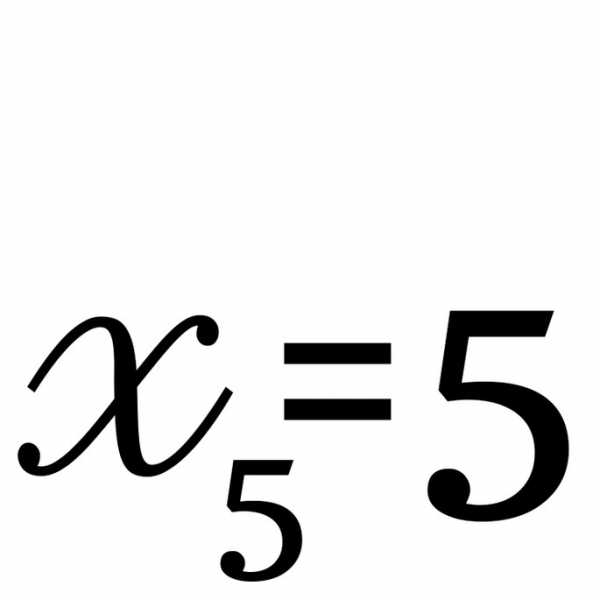, а потом взгляните на последующие элементы: 10-ый, 15-ый... Каждый пятый элемент делится на 5!

Первые 6 цифр Фибоначчи — 1/89

Если посчитать на калькуляторе 1 : 89 будет ответ 0,011235955... Заметили, что первые 6 цифр после запятой — ряд Фибоначчи?

День Фибоначчи 23/11

День Фибоначчи — 23 ноября (11/23; в американском формате дат месяц идёт первым, а день вторым), так как в нём присутствуют цифры "1, 1, 2, 3", которые являются частью последовательности. 23 ноября можно всех поздравлять с Днём Фибоначчи!

Смотрите также значения Числа Пи и Экспоненты.

Числа Фибоначчи: нескучные математические факты

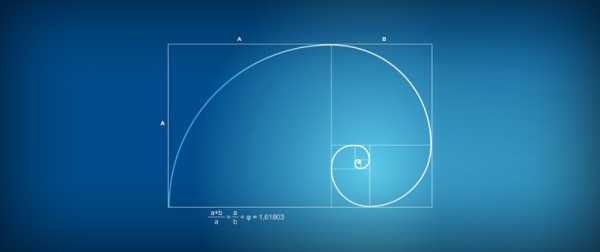
Вам, конечно же, знакома идея о том, что математика является самой главной из всех наук. Но многие могут с этим не согласиться, т.к. порой кажется, что математика – это лишь задачи, примеры и тому подобная скукотища. Однако математика может запросто показать нам знакомые вещи с совершенно незнакомой стороны. Мало того – она даже может раскрыть тайны мироздания. Как? Давайте обратимся к числам Фибоначчи.

Что такое числа Фибоначчи?

Числа Фибоначчи являются элементами числовой последовательности, где каждое последующее число образуется посредством суммирования двух предыдущих, например: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… Как правило, записывается такая последовательность формулой: F₀ = 0, F₁ = 1, F_n = F_n-1 + F_n-2, n ≥ 2.

Числа Фибоначчи могут начинаться и с отрицательных значений «n», но в таком случае последовательность будет двусторонней – она будет охватывать и положительные и отрицательные числа, стремясь к бесконечности в двух направлениях. Примером такой последовательности может послужить: -34, -21, -13, -8, -5, -3, -2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, а формула будет: F_n = F_n+1 — F_n+2 или же F_-n = (-1)ⁿ⁺¹Fn.

Создателем чисел Фибоначчи является один из первых математиков Европы средних веков по имени Леонардо Пизанский, которого, собственно и знают, как Фибоначчи – это прозвище он получил спустя много лет после своей смерти.

При жизни Леонардо Пизанский очень любил математические турниры, по причине чего в своих работах («Liber abaci» /«Книга абака», 1202; «Practica geometriae»/«Практика геометрии», 1220, «Flos»/«Цветок», 1225 год – исследование на тему кубических уравнений и «Liber quadratorum»/«Книга квадратов», 1225 – задачи о неопределенных квадратных уравнениях) очень часто разбирал всевозможные математические задачи.

О жизненном пути самого Фибоначчи известно крайне мало. Но достоверно известно то, что его задачи пользовались огромнейшей популярностью в математических кругах в последующие века. Одну из таких мы и рассмотрим далее.

Задача Фибоначчи с кроликами

Для выполнения задачи автором были поставлены следующие условия: есть пара новорождённых крольчат (самка и самец), отличающихся интересной особенностью – со второго месяца жизни они производят новую пару кроликов – тоже самку и самца. Кролики находятся в замкнутом пространстве и постоянно размножаются. И ни один кролик не умирает.

Задача: определить количество кроликов через год.

Решение:

У нас есть:

• Одна пара кроликов в начале первого месяца, которая спаривается в конце месяца
• Две пары кроликов во втором месяце (первая пара и потомство)
• Три пары кроликов в третьем месяце (первая пара, потомство первой пары с прошлого месяца и новое потомство)
• Пять пар кроликов в четвёртом месяце (первая пара, первое и второе потомство первой пары, третье потомство первой пары и первое потомство второй пары)

Количество кроликов в месяц «n» = количеству кроликов прошлого месяца + количество новых пар кроликов, другими словами, вышеназванная формула: F_n = F_n-1 + F_n-2. Отсюда получается рекуррентная числовая последовательность (о рекурсии мы скажем далее), где каждое новое число соответствует сумме двух предыдущих чисел:

1 месяц: 1 + 1 = 2

2 месяц: 2 + 1 = 3

3 месяц: 3 + 2 = 5

4 месяц: 5 + 3 = 8

5 месяц: 8 + 5 = 13

6 месяц: 13 + 8 = 21

7 месяц: 21 + 13 = 34

8 месяц: 34 + 21 = 55

9 месяц: 55 + 34 = 89

10 месяц: 89 + 55 = 144

11 месяц: 144 + 89 = 233

12 месяц: 233+ 144 = 377

И эта последовательность может продолжаться бесконечно долго, но учитывая, что задачей является узнать количество кроликов по истечении года, получается 377 пар.

Здесь важно также заметить, что одним из свойств чисел Фибоначчи является то, что если сопоставить две последовательные пары, а затем разделить большую на меньшую, то результат будет двигаться по направлению к золотому сечению, о котором мы также скажем ниже.

Пока же предлагаем вам ещё две задачи по числам Фибоначчи:

• Определить квадратное число, о котором известно только, что если отнять от него 5 или прибавить к нему 5, то снова выйдет квадратное число.
• Определить число, делящееся на 7, но при условии, что поделив его на 2, 3, 4, 5 или 6 в остатке будет 1.

Такие задачи не только станут отличным способом развития ума, но и занимательным времяпрепровождением. О том, как решаются эти задачи, вы также можете узнать, поискав информацию в Интернете. Мы же не будем заострять на них внимание, а продолжим наш рассказ.

Что же такое рекурсия и золотое сечение?

Рекурсия

Рекурсия является описанием, определением или изображением какого-либо объекта или процесса, в котором есть сам данный объект или процесс. Иначе говоря, объект или процесс можно назвать частью самого себя.

Рекурсия широко используется не только в математической науке, но также и в информатике, массовой культуре и искусстве. Применимо к числам Фибоначчи, можно сказать, что если число равно «n>2», то «n» = (n-1)+(n-2).

Золотое сечение

Золотое сечение является делением целого на части, соотносящиеся по принципу: большее относится к меньшему аналогично тому, как общая величина относится к большей части.

Впервые о золотом сечении упоминает Евклид (трактат «Начала» прим. 300 лет до н.э.), говоря и построении правильного прямоугольника. Однако более привычное понятие было введено немецким математиком Мартином Омом.

Приблизительно золотое сечение можно представить в качестве пропорционального деления на две разные части, к примеру, на 38% и 68%. Численное же выражение золотого сечения равно примерно 1,6180339887.

На практике золотое сечение используется в архитектуре, изобразительном искусстве (посмотрите работы Леонардо да Винчи), кино и других направлениях. На протяжении долгого времени, впрочем, как и сейчас, золотое сечение считалось эстетической пропорцией, хотя большинством людей оно воспринимается непропорциональным – вытянутым.

Вы можете попробовать оценить золотое сечение сами, руководствуясь следующими пропорциями:

• Длина отрезка a = 0,618
• Длина отрезка b= 0,382
• Длина отрезка c = 1
• Соотношение c и a = 1,618
• Соотношение c и b = 2,618

Теперь же применим золотое сечение к числам Фибоначчи: берём два соседних члена его последовательности и делим большее на меньшее. Получаем примерно 1,618. Если же возьмём то же самое большее число и поделим его на следующее большее за ним, то получим примерно 0,618. Попробуйте сами: «поиграйте» с числами 21 и 34 или какими-то другими. Если же провести этот опыт с первыми числами последовательности Фибоначчи, то такого результата уже не будет, т.к. золотое сечение «не работает» в начале последовательности. Кстати, чтобы определить все числа Фибоначчи, нужно знать всего лишь три первых последовательных числа.

И в заключение ещё немного пищи для ума.

Золотой прямоугольник и спираль Фибоначчи

«Золотой прямоугольник» — это ещё одна взаимосвязь между золотым сечением и числами Фибоначчи, т.к. соотношение его сторон равно 1,618 к 1 (вспоминайте число 1,618!).

Вот пример: берём два числа из последовательности Фибоначчи, например 8 и 13, и чертим прямоугольник с шириной 8 см и длинной 13 см. Далее разбиваем основной прямоугольник на мелкие, но их длина и ширина должна соответствовать числам Фибоначчи – длина одной грани большого прямоугольника должна равняться двум длинам грани меньшего.

После этого соединяем плавной линией углы всех имеющихся у нас прямоугольников и получаем частный случай логарифмической спирали – спираль Фибоначчи. Её основными свойствами являются отсутствие границ и изменение форм. Такую спираль можно часто встретить в природе: самыми яркими примерами являются раковины моллюсков, циклоны на изображениях со спутника и даже ряд галактик. Но более интересно то, что этому же правилу подчиняется и ДНК живых организмов, ведь вы помните, что оно имеет спиралевидную форму?

Эти и многие другие «случайные» совпадения даже сегодня будоражат сознание учёных и наводят на мысль о том, что всё во Вселенной подчинено единому алгоритму, причём, именно математическому. И эта наука кроет в себе огромное количество совсем нескучных тайн и загадок.

---

Смотрите также

• 
  Что такое топографическая съемка это
• 
  Анализ крови аст что это такое как понизить
• 
  Подводные кольца что это такое
• 
  Узел в матке что это такое
• 
  Ендова крыши что это такое
• 
  Биометрический контроль для иностранцев что это такое
• 
  Финансовый консалтинг что это такое
• 
  Парацервикальные кисты шейки матки что это такое
• 
  Гаммаглобулин что это такое
• 
  Фолликулярная эрозия шейки матки что это такое
• 
  Фид канала что это такое