Преобразование фурье что это такое

Преобразование Фурье — Википедия

Преобразование Фурье (символ ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами (подобно тому, как музыкальный аккорд может быть выражен в виде суммы музыкальных звуков, которые его составляют).

Преобразование Фурье функции f{\displaystyle f} вещественной переменной является интегральным и задаётся следующей формулой:

f^(ω)=12π∫−∞∞f(x)e−ixωdx.{\displaystyle {\hat {f}}(\omega )={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }f(x)e^{-ix\omega }\,dx.}

Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.

Кроме того, существуют разнообразные обобщения данного понятия (см. ниже).

Хотя формула, задающая преобразование Фурье, имеет ясный смысл только для функций класса L1(R){\displaystyle L_{1}(\mathbb {R} )}, преобразование Фурье может быть определено и для более широкого класса функций и даже обобщённых функций. Это возможно благодаря ряду свойств преобразования Фурье:

(αf+βg)^=αf^+βg^.{\displaystyle {\widehat {(\alpha f+\beta g)}}=\alpha {\hat {f}}+\beta {\hat {g}}.}

• Справедливо равенство Парсеваля: если f∈L1(R)∩L2(R){\displaystyle f\in L_{1}(\mathbb {R} )\cap L_{2}(\mathbb {R} )}, то преобразование Фурье сохраняет L2{\displaystyle L_{2}}-норму:

∫−∞∞|f(x)|2dx=∫−∞∞|f^(w)|2dω.{\displaystyle \int \limits _{-\infty }^{\infty }|f(x)|^{2}\,dx=\int \limits _{-\infty }^{\infty }|{{\hat {f}}(w)}|^{2}\,d\omega .}

Это свойство позволяет по непрерывности распространить определение преобразования Фурье на всё пространство L2(R){\displaystyle L_{2}(\mathbb {R} )}. Равенство Парсеваля будет при этом справедливо для всех f∈L2(R){\displaystyle f\in L_{2}(\mathbb {R} )}.

• Формула обращения:

f(x)=12π∫−∞∞f^(ω)eixωdω{\displaystyle f(x)={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }{\hat {f}}(\omega )e^{ix\omega }\,d\omega }

справедлива, если интеграл в правой части имеет смысл. В частности, это верно, если функция f{\displaystyle f} является достаточно гладкой. Если f∈L2(R){\displaystyle f\in L_{2}(\mathbb {R} )}, то формула также верна, поскольку равенство Парсеваля позволяет придать интегралу в правой части смысл с помощью предельного перехода.

Эта формула объясняет физический смысл преобразования Фурье: правая часть — (бесконечная) сумма гармонических колебаний eiωx{\displaystyle e^{i\omega x}} с частотами ω{\displaystyle \omega }, амплитудами 12π|f^(ω)|{\displaystyle {\frac {1}{\sqrt {2\pi }}}|{\hat {f}}(\omega )|} и фазовыми сдвигами arg⁡f^(ω){\displaystyle \arg {\hat {f}}(\omega )} соответственно.

• Теорема о свёртке: если f,g∈L1(R){\displaystyle f,\;g\in L_{1}(\mathbb {R} )}, тогда

(f∗g)^=2πf^g^{\displaystyle {\widehat {(f\ast g)}}={\sqrt {2\pi }}{\widehat {f}}{\widehat {g}}}, где

(f∗g)(t)=∫−∞∞f(t−s)g(s)ds.{\displaystyle (f\ast g)(t)=\int \limits _{-\infty }^{\infty }f(t-s)g(s)\,ds.}

Эта формула может быть распространена и на случай обобщённых функций.

• Преобразование Фурье и дифференцирование. Если f,f′∈L1(R){\displaystyle f,\;f'\in L_{1}(\mathbb {R} )}, то

(f′)^=iωf^.{\displaystyle {\widehat {(f')}}=i\omega {\widehat {f}}.}

Из этой формулы легко выводится формула для n{\displaystyle n}-й производной:

(f(n))^=(iω)nf^.{\displaystyle {\widehat {(f^{(n)})}}=(i\omega )^{n}{\widehat {f}}.}

Формулы верны и в случае обобщённых функций.

• Преобразование Фурье и сдвиг.

f(x−x0)^=e−iωx0f^(ω).{\displaystyle {\widehat {f(x-x_{0})}}=e^{-i\omega x_{0}}{\hat {f}}(\omega ).}

Эта и предыдущая формула являются частными случаями теоремы о свёртке, так как сдвиг по аргументу — это свёртка со сдвинутой дельта-функцией δ(x−x0){\displaystyle \delta (x-x_{0})}, а дифференцирование — свёртка с производной дельта-функции.

• Преобразование Фурье и растяжение.

f(ax)^=|a|−1f^(ω/a).{\displaystyle {\widehat {f(ax)}}=|a|^{-1}{\hat {f}}(\omega /a).}

• Преобразование Фурье обобщённых функций. Преобразование Фурье можно определить для широкого класса обобщённых функций. Определим вначале пространство гладких быстро убывающих функций (пространство Шварца):

S(R):={φ∈C∞(R):∀n,m∈Nxnφ(m)(x)→x→∞0}.{\displaystyle S(\mathbb {R} ):=\left\{\varphi \in C^{\infty }(\mathbb {R} ):\forall n,\;m\in \mathbb {N} \;x^{n}\varphi ^{(m)}(x){\xrightarrow {x\to \infty }}0\right\}.}

Ключевым свойством этого пространства является то, что это инвариантное подпространство по отношению к преобразованию Фурье.

Теперь определим его двойственное пространство S∗(R){\displaystyle S^{*}(\mathbb {R} )}. Это некоторое подпространство в пространстве всех обобщённых функций — так называемые обобщённые функции медленного роста. Теперь для функции f∈S∗(R){\displaystyle f\in S^{*}(\mathbb {R} )} её преобразованием Фурье называется обобщённая функция f^∈S∗(R){\displaystyle {\hat {f}}\in S^{*}(\mathbb {R} )}, действующая на основные функции по правилу

⟨f^,φ⟩=⟨f,φ^⟩.{\displaystyle \langle {\hat {f}},\;\varphi \rangle =\langle f,\;{\hat {\varphi }}\rangle .}

Например, вычислим преобразование Фурье дельта-функции:

⟨δ^,φ⟩=⟨δ,φ^⟩=⟨δ,12π∫−∞∞φ(x)e−iωxdx⟩=12π∫−∞∞φ(x)⋅1dx=⟨12π,φ⟩.{\displaystyle \langle {\hat {\delta }},\;\varphi \rangle =\langle \delta ,\;{\hat {\varphi }}\rangle =\left\langle \delta ,\;{\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }\varphi (x)e^{-i\omega x}\,dx\right\rangle ={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }\varphi (x)\cdot 1\,dx=\left\langle {\frac {1}{\sqrt {2\pi }}},\;\varphi \right\rangle .}

Таким образом, преобразованием Фурье дельта-функции является константа 12π{\displaystyle {\frac {1}{\sqrt {2\pi }}}}.

Преобразование Фурье используется во многих областях науки — в физике, теории чисел, комбинаторике, обработке сигналов, теории вероятностей, статистике, криптографии, акустике, океанологии, оптике, геометрии и многих других. В обработке сигналов и связанных областях преобразование Фурье обычно рассматривается как декомпозиция сигнала на частоты и амплитуды, то есть обратимый переход от временно́го пространства (time domain) в частотное пространство (frequency domain). Богатые возможности применения основываются на нескольких полезных свойствах преобразования:

• Преобразования являются линейными операторами и, с соответствующей нормализацией, унитарными (свойство, известное как теорема Парсеваля, или, в более общем случае, как теорема Планшереля, или, в наиболее общем, как дуализм Понтрягина).
• Преобразования обратимы, причём обратное преобразование имеет практически такую же форму, как и прямое преобразование.
• Синусоидальные базисные функции (вернее, комплексные экспоненты) являются собственными функциями дифференцирования, что означает, что данное представление превращает линейные дифференциальные уравнения с постоянными коэффициентами в обычные алгебраические. (Например, в линейной стационарной системе частота — консервативная величина, поэтому поведение на каждой частоте может решаться независимо).
• По теореме о свёртке, преобразование Фурье превращает сложную операцию свёртки в простое умножение, что означает, что они обеспечивают эффективный способ вычисления основанных на свёртке операций, таких как умножение многочленов и умножение больших чисел.
• Дискретная версия преобразования Фурье может быть быстро рассчитана на компьютерах с использованием алгоритма быстрого преобразования Фурье (БПФ, англ. FFT).

Многомерное преобразование[править | править код]

Преобразование Фурье функций, заданных на пространстве Rn{\displaystyle \mathbb {R} ^{n}}, определяется формулой

f^(ω)=1(2π)n/2∫Rnf(x)e−ix⋅ωdx.{\displaystyle {\hat {f}}(\omega )={\frac {1}{(2\pi )^{n/2}}}\int \limits _{\mathbb {R} ^{n}}f(x)e^{-ix\cdot \omega }\,dx.}

Здесь ω{\displaystyle \omega } и x{\displaystyle x} — векторы пространства Rn{\displaystyle \mathbb {R} ^{n}}, x⋅ω{\displaystyle x\cdot \omega } — их скалярное произведение. Обратное преобразование в этом случае задается формулой

f(x)=1(2π)n/2∫Rnf^(ω)eix⋅ωdω.{\displaystyle f(x)={\frac {1}{(2\pi )^{n/2}}}\int \limits _{\mathbb {R} ^{n}}{\hat {f}}(\omega )e^{ix\cdot \omega }\,d\omega .}

Эта формула может быть интерпретирована как разложение функции f{\displaystyle f} в линейную комбинацию (суперпозицию) «плоских волн» вида eix⋅ω{\displaystyle e^{ix\cdot \omega }} с амплитудами 1(2π)n/2|f^(ω)|{\displaystyle {\frac {1}{(2\pi )^{n/2}}}|{\hat {f}}(\omega )|}, частотами ω{\displaystyle \omega } и фазовыми сдвигами arg⁡f^(ω){\displaystyle \arg {\hat {f}}(\omega )} соответственно. Как и прежде, в разных источниках определения многомерного преобразования Фурье могут отличаться выбором константы перед интегралом.

Замечание относительно области задания преобразования Фурье и его основные свойства остаются справедливыми и в многомерном случае, со следующими уточнениями:

• Взятие частных производных под действием преобразования Фурье превращается в умножение на одноимённую координату:

∂f∂xk^=iωkf^(ω).{\displaystyle {\widehat {\frac {\partial f}{\partial x_{k}}}}=i\omega _{k}{\hat {f}}(\omega ).}

• Изменяется константа в теореме о свёртке:

(f∗g)^=(2π)n/2f^g^.{\displaystyle {\widehat {(f\ast g)}}=(2\pi )^{n/2}{\hat {f}}{\hat {g}}.}

• Преобразование Фурье и сжатие координат:

(f(x|a|))^=|a|nf^(ω|a|).{\displaystyle {\widehat {\left(f\left({\frac {x}{|a|}}\right)\right)}}=|a|^{n}{\hat {f}}(\omega |a|).}

(f(Ax))^=|det(A)|−1f^((AT)−1ω).{\displaystyle {\widehat {\left(f(Ax)\right)}}=|\det(A)|^{-1}{\hat {f}}((A^{T})^{-1}\omega ).}

Ряды Фурье[править | править код]

Непрерывное преобразование само фактически является обобщением более ранней идеи рядов Фурье, которые определены для 2π{\displaystyle 2\pi }-периодических функций и представляют собой разложение таких функций в (бесконечную) линейную комбинацию гармонических колебаний с целыми частотами:

f(x)=∑n=−∞∞f^neinx.{\displaystyle f(x)=\sum _{n=-\infty }^{\infty }{\hat {f}}_{n}\,e^{inx}.}

Разложение в ряд Фурье применимо также к функциям, заданным на ограниченных промежутках, поскольку такие функции могут быть периодически продолжены на всю прямую.

Ряд Фурье является частным случаем преобразования Фурье, если последнее понимать в смысле обобщённых функций. Для любой 2π{\displaystyle 2\pi }-периодической функции имеем

f^(ω)=2π∑n=−∞∞f^nδ(ω−n).{\displaystyle {\hat {f}}(\omega )={\sqrt {2\pi }}\sum _{n=-\infty }^{\infty }{\hat {f}}_{n}\delta (\omega -n).}

Иными словами, преобразование Фурье периодической функции представляет собой сумму точечных нагрузок в целых точках, и равно нулю вне их.

Дискретное преобразование[править | править код]

Дискретное преобразование Фурье — преобразование конечных последовательностей (комплексных) чисел, которое, как и в непрерывном случае, превращает свёртку в поточечное умножение. Используется в цифровой обработке сигналов и в других ситуациях, где необходимо быстро выполнять свёртку, например, при умножении больших чисел.

Пусть x0,x1,…,xn−1{\displaystyle x_{0},\;x_{1},\;\ldots ,\;x_{n-1}} — последовательность комплексных чисел. Рассмотрим многочлен f(t)=x0+x1t+x2t2+…+xn−1tn−1{\displaystyle f(t)=x_{0}+x_{1}t+x_{2}t^{2}+\ldots +x_{n-1}t^{n-1}}. Выберем какие-нибудь n{\displaystyle n} точек на комплексной плоскости z0,z1,…,zn−1{\displaystyle z_{0},\;z_{1},\;\ldots ,\;z_{n-1}}. Теперь многочлену f(t){\displaystyle f(t)} мы можем сопоставить новый набор из n{\displaystyle n} чисел: f0:=f(z0),f1:=f(z1),…,fn−1:=f(zn−1){\displaystyle f_{0}:=f(z_{0}),\;f_{1}:=f(z_{1}),\;\ldots ,\;f_{n-1}:=f(z_{n-1})}. Заметим, что это преобразование обратимо: для любого набора чисел

Простыми словами о преобразовании Фурье / Habr

Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.

(с) xkcd

Без использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:

• FT, DTF, DTFT — в чем отличия и как совершенно разные казалось бы формулы дают столь концептуально похожие результаты?
• Как правильно интерпретировать результаты быстрого преобразования Фурье (FFT)
• Что делать если дан сигнал из 179 сэмплов а БПФ требует на вход последовательность по длине равную степени двойки
• Почему при попытке получить с помощью Фурье спектр синусоиды вместо ожидаемой одиночной “палки” на графике вылезает странная загогулина и что с этим можно сделать
• Зачем перед АЦП и после ЦАП ставят аналоговые фильтры
• Можно ли оцифровать АЦП сигнал с частотой выше половины частоты дискретизации (школьный ответ неверен, правильный ответ — можно)
• Как по цифровой последовательности восстанавливают исходный сигнал

Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”

Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):

Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:

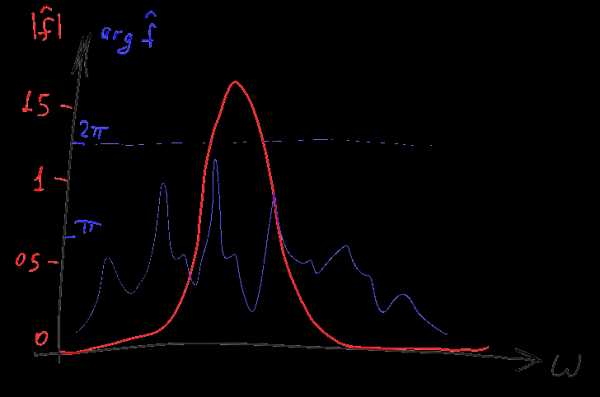
График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).

Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.

Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.

Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:

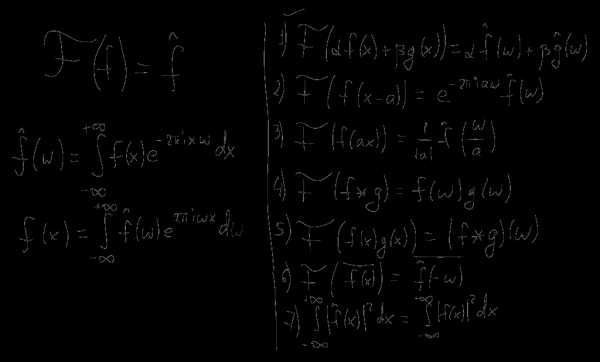
Первое из этих свойств — линейность. Если мы берем какую-то линейную комбинацию функций, то преобразование Фурье этой комбинации будет такой же линейной комбинацией образов Фурье этих функций. Это свойство позволяет сводить сложные функции и их фурье-образы к более простым. Например, фурье-образ синусоидальной функции с частотой f и амплитудой a является комбинацией из двух дельта-функций расположенных в точках f и -f и с коэффициентом a/2:

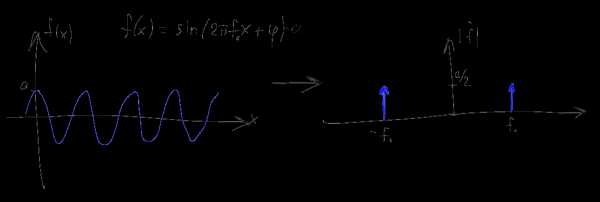
Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.

Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.

Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.

Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.

Шестое свойство говорит о симметрии фурье-образов. В частности, из этого свойства следует что в фурье-образе действительнозначной функции (т.е. любого “реального” сигнала) амплитудный спектр всегда является четной функцией, а фазовый спектр (если его привести к диапазону -pi...pi) — нечетной. Именно по этой причине на графиках спектров практически никогда не рисуют отрицательную часть спектра — для действительнозначных сигналов она не дает никакой новой информации (но, повторюсь, и нулевой при этом не является).

Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).

Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:

Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T<<1. Фурье-образ этой функции — тоже гребенка Дирака, только с гораздо большим шагом 1/T и несколько меньшим коэффициентом (1/T). С математической точки зрения, дискретизация сигнала по времени — это просто поточечное умножение исходного сигнала на гребенку Дирака. Значение 1/T при этом называют частотой дискретизации:

Вместо непрерывной функции после подобного перемножения получается последовательность дельта-импульсов определенной высоты. При этом согласно свойству 5 преобразования Фурье, спектр получившегося дискретного сигнала есть свертка исходного спектра с соответствующей гребенкой Дирака. Несложно понять, что исходя из свойств свертки, спектр исходного сигнала при этом как бы “копируется” бесконечное число раз вдоль оси частот с шагом 1/T, а затем суммируется.

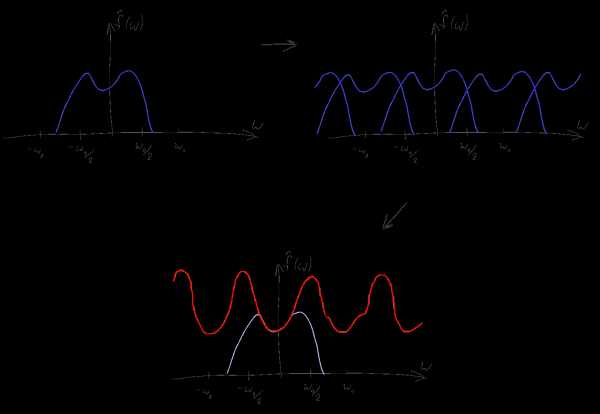
Заметим, что если исходный спектр имел конечную ширину и мы использовали достаточно большую частоту дискретизации, то копии исходного спектра не будут перекрываться, а следовательно и суммироваться друг с другом. Несложно понять что по подобному “свернутому” спектру будет легко восстановить исходный — достаточно будет просто взять компоненту спектра в районе нуля, “обрезав” лишние копии уходящие на бесконечность. Простейший способ это сделать — это домножить спектр на прямоугольную функцию, равную T в диапазоне -1/2T...1/2T и нулю — вне этого диапазона. Подобный Фурье-образ соответствует функции sinc(Tx) и согласно свойству 4, подобное умножение равнозначно свертке исходной последовательности дельта-функций с функцией sinc(Tx)

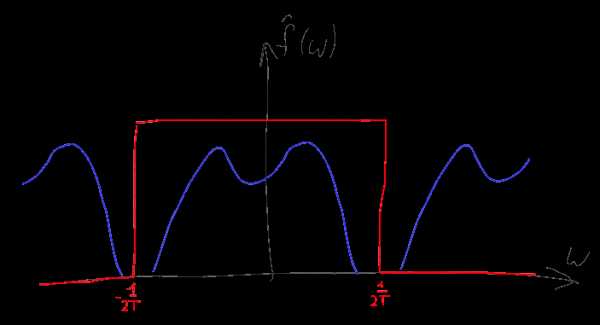
То есть с помощью преобразования Фурье мы получили способ легко восстановить исходный сигнал из дискретизированного по времени, работающий при условии что мы используем частоту дискретизации, по крайней мере вдвое (из-за наличия в спектре отрицательных частот) превышающую максимальную частоту присутствующую в исходном сигнале. Этот результат широко известен и называется “теорема Котельникова / Шеннона-Найквиста”. Однако, как несложно теперь (понимая доказательство) заметить, этот результат вопреки широко распространенному заблуждению определяет достаточное, но не необходимое условие для восстановления исходного сигнала. Все что нам требуется — это добиться того, чтобы интересующая нас часть спектра после дискретизации сигнала не накладывалась друг на друга и если сигнал достаточно узкополосный (имеет малую “ширину” ненулевой части спектра), то этого результата часто можно добиться и при частоте дискретизации намного ниже чем удвоенная максимальная частота сигнале. Подобная техника называется “undersampling” (субдискретизация, полосовая дискретизация) и довольно широко используется при обработке всевозможных радиосигналов. Например, если мы берем FM-радио действующее в полосе частот от 88 до 108 МГц, то для его оцифровки можно использовать АЦП с частотой всего 43.5 МГц вместо предполагающихся по теореме Котельникова 216 МГц. При этом, правда, понадобится качественный АЦП и хороший фильтр.

Замечу, что “дублирование” высоких частот частотами меньших порядков (алиасинг) — непосредственное свойство дискретизации сигнала, необратимо “портящее” результат. Поэтому если в сигнале в принципе могут присутствовать частоты высокого порядка (то есть практически всегда) перед АЦП ставят аналоговый фильтр, “отсекающий” все лишнее непосредственно в исходном сигнале (так как после дискретизации делать это уже будет поздно). Характеристики этих фильтров, как аналоговых устройств, неидеальны, поэтому некоторая “порча” сигнала при этом все равно происходит, и на практике из этого следует что наибольшие частоты в спектре, как правило, недостоверны. Чтобы уменьшить эту проблему, сигнал нередко сэмплируют с завышенной частотой дискретизации, ставя при этом входной аналоговый фильтр на меньшую полосу пропускания и используя только нижнюю часть теоретически доступного частотного диапазона АЦП.

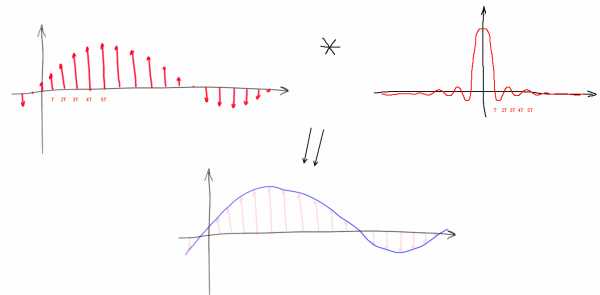
Еще одно распространенное заблуждение, кстати, — это когда сигнал на выходе ЦАП рисуют “ступеньками”. “Ступеньки” соответствуют свертке дискретизированной последовательности сигналов с прямоугольной функцией ширины T и высоты 1:

Спектр сигнала при таком преобразовании умножается на фурье-образ этой прямоугольной функции, а у подобной прямоугольной функции это снова sinc(w), “растянутый” тем сильнее, чем меньше ширина соответствующего прямоугольника. Спектр дискретизированного сигнала при подобном “ЦАП” поточечно умножается на этот спектр. При этом ненужные высокие частоты с “лишними копиями” спектра обрезаются не полностью, а верхняя часть “полезной” части спектра, напротив, ослабляется.

На практике так, естественно, никто не делает. Существует много разных подходов к построению ЦАП, но даже в наиболее близких по смыслу ЦАП взвешивающего типа прямоугольные импульсы в ЦАП напротив выбираются по возможности короткими (приближающимися к настоящей последовательности дельта-функций) чтобы избежать излишнего подавления полезной части спектра. “Лишние” частоты в получившемся широкополосном сигнале практически всегда гасят, пропуская сигнал через аналоговый фильтр низких частот, так что «цифровых ступенек» нет ни «внутри» преобразователя, ни, тем более, на его выходе.

Однако вернемся обратно к преобразованию Фурье. Описанное выше преобразование Фурье, примененное к заранее дискретизированной последовательности сигналов называется преобразованием Фурье дискретного времени (DTFT). Спектр получаемый подобным преобразованием всегда 1/T-периодичен, поэтому спектр DTFT полностью определяется её значениями на отрезке [0...1/T), поэтому часто этим отрезком спектр DTFT и ограничивают. При этом результат DTFT несмотря на то что это спектр дискретизированного сигнала — по-прежнему “аналоговая” функция. Кроме того, для “обычных” действительнозначных сигналов вторая половина этого спектра в силу свойства 6 зеркально повторяет левую половину, отраженную относительно частоты Найквиста 1/2T.

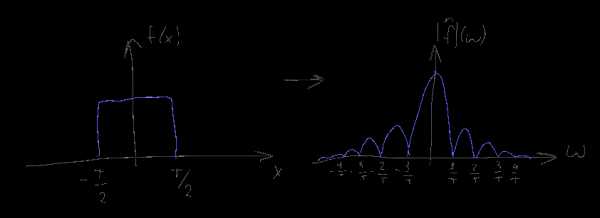
До сих пор мы предполагали что на вход наших преобразований поступает сигнал определенный от минус до плюс бесконечности. Однако реальные доступные нам сигналы всегда имеют конечную длину — что делать? Для решения этой проблемы в FT и DTFT конечный сигнал просто дополняют слева и справа на бесконечность нулями. Если исходный сигнал изначально был конечным (скажем, это отдельный импульс) и в преобразование Фурье он попал полностью, то этот подход напрямую дает желаемый результат. Однако часто «конечный» сигнал используемый для преобразования Фурье на самом деле является частью более длинного, возможно бесконечного сигнала, такого как, например, синусоида. В этом случае дополнение конечного отрезка нулями интерпретируют следующим образом: считают что исходный сигнал имеет бесконечно большую длину, но затем умножается на некоторую взвешивающую функцию — “окно”, обращающуюся в ноль вне доступного нам для измерения отрезка. В простейшем случае роль “окна” играет просто прямоугольная функция, соответствующая тому что мы просто дополняем конечный сигнал слева и справа бесконечным числом нулей. В более сложных — исходную последовательность умножают на весовые коэффициенты определяемые функцией “окна” и затем, опять же, дополняют нулями.

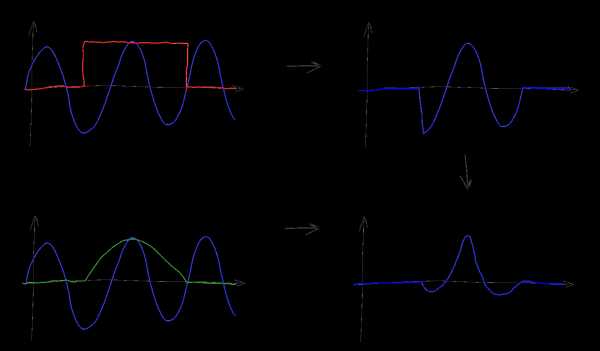
Пользуясь уже хорошо нам знакомым свойством 5, несложно сообразить, что при подобном умножении исходный сигнал прсто сворачивается со спектром функции окна. Например если мы пытаемся измерить спектр синусоиды (дельта-функцию), но ограничиваем интервал измерений прямоугольным окном, то в получившимся спектре на месте дельта-функции мы увидим спектр окна — т.е. Tsinc(T(x-f)):

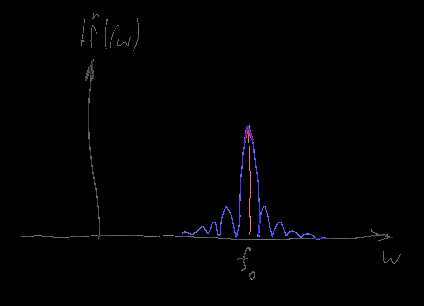
В данном случае T — это длина интервала которым мы ограничили наш сигнал, так что чем длиннее будет входной сигнал — тем “уже” и ближе к истинной дельта-функции будет наблюдаемый нами спектр. Конечная “ширина” главного лепестка приводит к невозможности уверенно различать наличие в исходном сигнале синусоид близких друг к другу по частоте, а наличие “боковых лепестков” вносит небольшие искажения и в далеко расположенные частоты, мешая точному измерению амплитуды отдельных частот, особенно если нужно измерять спектр в областях небольшой амплитуды при наличии в спектре на порядок более мощных компонент. Этот эффект называют “спектральной утечкой” и полностью победить его для бесконечных сигналов невозможно, но чем длиннее интервал на котором измеряется сигнал — тем меньше влияние этой утечки. Выбором функции окна можно контролировать “ширину” этой утечки, либо концентрируя её вокруг главной частоты (сильно “размывая” спектр, но зато не мешая соседним частотам), либо размазывая её повсюду (размытие пиков уменьшается но сильно растет “шум” и как следствие — погрешность измерения амплитуды отдельных частот). Заметьте, что выбранная частота дискретизации в спектральной утечке почти не играет роли — короткий отрезок сигнала можно сэмплировать хоть на 10 ГГц, но это увеличит только количество поддающихся измерению частот, тогда как точность определения каждой отдельной частоты все равно останется низкой.

Интересным частным случаем является ситуация, в которой сигнал с набором дискретных частот nF дискретизируется на частоте mF, где m,n — целые числа. В этом случае нули “окна” и расположение дельта-функций в спектре в точности совпадают и хотя частоты все равно “размазываются”, но их амплитуда в точках mF совпадает с истинной — “шум” равен нулю. Это свойство позволяет доказать аналог теоремы Котельникова для дискретного преобразования Фурье, но на практике такие сигналы, к сожалению, фактически не встречаются.

Итак, со “входом” мы разобрались — из непрерывной функции бесконечной длины мы получили конечное число дискретных отсчетов, с которыми можем работать а взамен получили ограничения по ширине спектра и утечку частот. Однако “выход” DTFT по-прежнему является непрерывной функцией, работать с которой компьютеру проблематично. На практике эту проблему решают очень просто — полный отрезок [0,1/T) делят на k равных частей и считают DTFT в точках fi=i/kT, где i = 0,1,… k-1. Получившуюся конструкцию называют “дискретным преобразованием Фурье” (DFT).

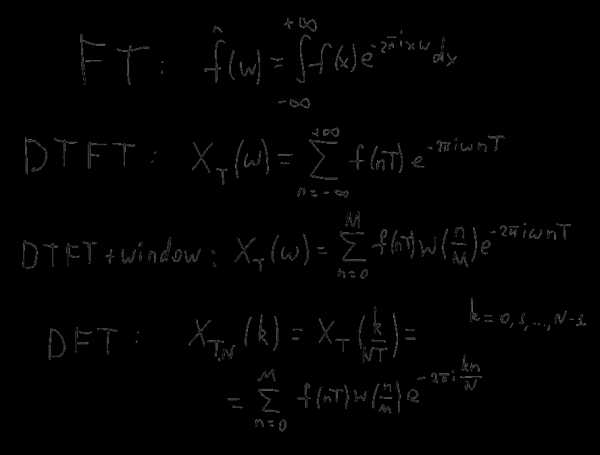
Последнее преобразование удобно нормализовать, убрав из него T и вопросы связанные с выбором “окна”. Эту нормализованную запись часто используют в качестве определения DFT как преобразования последовательности из N комплексных чисел:

Прелесть преобразования Фурье записанного в такой форме — в том что сохраняя все достоинства DTFT, подобное DTF для “гладких” k (например, степеней двойки) можно вычислять чрезвычайно быстро, за время порядка k log(k). Соответствующие алгоритмы называют “быстрым преобразованием Фурье” (БПФ, FFT) и их, вообще говоря, существует несколько. С практической точки зрения, впрочем, их все можно рассматривать как “черные ящики”, получающие последовательность комплексных чисел на входе и выдающих последовательность комплексных чисел на выходе. Таким образом, работа с дискретизированным сигналом конечной длины сводится к тому, что этот сигнал вначале умножается на подходящую взвешивающую функцию, затем дополняется нужным числом нулей справа и передается в алгоритм БПФ.

Как интерпретировать получившийся результат? С учетом всего вышеизложенного,

• Получившиеся значения есть равномерная сетка отсчетов по спектру DTFT. Чем больше отсчетов — тем мельче сетка, тем подробнее виден спектр. Дописывая к известной последовательности нужное число нулей можно посчитать сколь угодно близкое приближение к непрерывному спектру
• Спектр DTFT задан на отрезке частот от 0 до 1/T (где 1/T — частота дискретизации) и периодически повторяется на бесконечность вне этого отрезка
• Этот спектр задан комплексными числами (парами действительных). Амплитуда определяется как модуль комплексного числа, фаза — как аргумент.
• Для действительнозначного входного сигнала, спектр в диапазоне 1/2T...1/T просто зеркально повторяет спектр 0...1/2T и не несет соответственно полезной нагрузки (для визуализации спектра его можно просто обрезать)
• Если исходный сигнал содержал частоты выше половины частоты дискретизации, то они будут отображены в более низкие частоты (возможно накладываясь поверх уже существующего сигнала этой частоты) — алиасинг
• В спектре всегда присутствует “спектральная утечка” определяющаяся выбранной взвешивающей “оконной функцией”. Чем длиннее исходный сигнал (до дополнения нулями!) — тем эта утечка меньше.
• Спектральная утечка ограничивает осмысленность расчета БПФ с большим дополнением нулями. Однако дополнение все же часто бывает полезным, поскольку, например, позволяет точнее определить максимум узкополосного синусоидального сигнала, если он не попадает точно в одну из частот вида k/T.
• Синусоиде амплитуды A в амплитудном спектре (при выбранной мной нормировке преобразования Фурье) соответствует значение A*N/2, за исключением нулевой частоты, которая не раскладывается на “плюс” и “минус” частоту и потому имеет амплитуду A*N, а также частоты Найквиста 1/2T в которой касаются в предельном случае друг друга отдельные копии спектра (там тоже будет A*N, но, в отличие от нуля в выход БПФ это значение не попадает да и достоверным в реальных схемах все равно никогда не является). Здесь N = T1/T0, где T1 — это длина исходного сигнала (она определяет коэффициент перед спектром «окна»), а T0 — длина одного периода дискретизации (она определяет коэффициент у гребенки Дирака) и по смыслу это, как несложно видеть, попросту число отсчетов в исходном сигнале (до его дополнения нулями)

Ну вот, в общем, и всё. Надеюсь преобразование Фурье и алгоритмы БПФ будут теперь для Вас простыми, понятными и приятными в обращении инструментами.

Преобразование Фурье: самый подробный разбор

Преобразование Фурье – одно из базовых понятий в обработке сигналов и анализе данных. Но что оно означает? Геометрическая интерпретация.

Возьмём классическую задачу – работу со звуком. Теперь добавим конкретики.

Ваш друг приносит запись своего живого выступления. И это очень удачное выступление. Но! Хотя запись делали на хороший микрофон, в ней всё равно присутствует шум. Друг просит помочь убрать его или хотя бы уменьшить.

Здесь и пригодится знание преобразования Фурье.

Что такое звук в математическом смысле?

Отдельная нота – это гармонический сигнал с определённой частотой и амплитудой.

Как правило, мелодию, речь или иной звуковой сигнал можно представить как сумму гармонических сигналов. Шумом в таком случае мы называем слагаемые, соответствующие любым нежелательным звукам.

Преобразование Фурье позволяет разложить исходный сигнал на гармонические составляющие, что потребуется для выделения шумов.

Запишем определение:

Здесь g(t) – это исходный сигнал (в нашем случае запись друга). В контексте преобразования Фурье его называют оригиналом. G(f) – изображение по Фурье, а параметром f выступает частота.

Возможно, вам уже знакомо это определение. Но знаете ли вы, как происходит это преобразование? Если бы увидели его впервые, поняли бы, как с его помощью анализировать исходный сигнал?

Геометрическая интерпретация преобразования Фурье

Грант Сандерсон предлагает геометрический аналог преобразования Фурье. За несколько графических переходов от исходного сигнала к изображению каждая из компонент определения обретает смысл, а само преобразование получает новое геометрическое прочтение.

В дальнейшем обсуждении предполагается, что вы знакомы с векторами, интегрированием и понятием комплексного числа. Если каких-то знаний вам всё-таки не хватает, ознакомьтесь с материалами из нашей подборки по вузовской математике.

1. Наматываем сигнал

Давайте начнём с самого простого случая. Рассмотрим гармонический сигнал, совершающий 3 колебания в секунду (f₀ = 3с^-1):

g(t) = 1 + cos (6πt).

Отобразим g(t) на комплексную плоскость. Для этого введём радиус-вектор, который равномерно вращается по часовой стрелке. Его длина в каждый момент времени равна модулю значения сигнала, а частота вращения выбирается произвольным образом.

Теперь построим траекторию движения конца вектора, совершающего полный оборот за две секунды, или, другими словами, с частотой вращения f_В = 0.5 об/с.

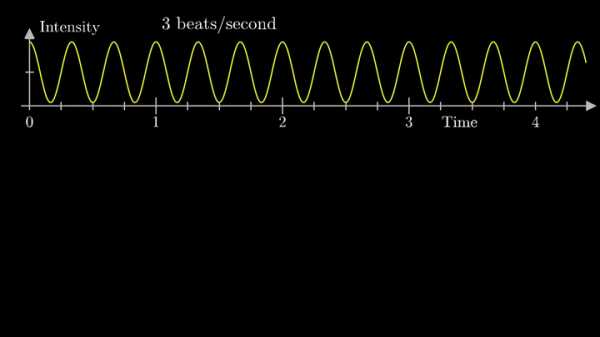
Выглядит, будто мы намотали исходный сигнал на начало координат. В минимумах сигнала полученная "намотка" сливается с началом координат, а при приближении к максимумам – отклоняется.

Пока выглядит не особо информативно, не так ли?

А теперь увеличим частоты намотки.

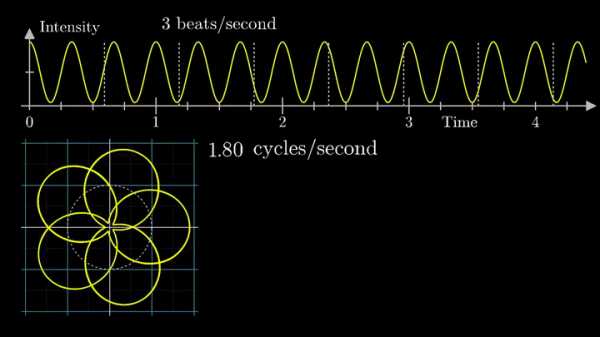
Сначала график распределяется довольно симметрично относительно начала координат до частоты вращения f_В = 3 об/с. Затем максимумы резко смещаются в правую полуплоскость, а намотка перестаёт напоминать узор спирографа.

2. Ищем центр масс

Посмотрим внимательнее, что происходит. В качестве характеристики намотки возьмём усреднённое значение всех её точек – центр масс (отметим его оранжевым цветом).

Строим зависимость положения центра масс от частоты намотки. Сейчас нам достаточно рассмотреть х-кординату, но в дальнейшем для определения преобразования Фурье потребуются обе координаты.

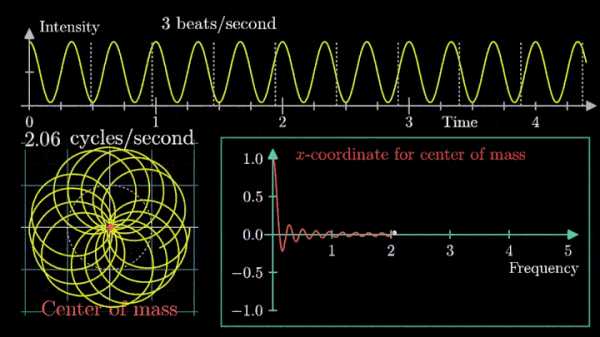
Мы видим два пика: в точках f_В = 0 об/с и f_В = 3 об/с. На основании такого поведения центра масс уже можно судить о частоте исходного сигнала (он колеблется с f = 3с^-1).

Тогда что означает всплеск на низких частотах?

3. Анализируем влияние смещения

Возможно, вы обратили внимание, что рассматриваемый нами сигнал смещён на единицу. Сдвиг был введён для наглядности, но именно он приводит к усложнению поведения центра масс.

При нулевой частоте всё отображение сигнала на комплексной плоскости располагается на оси абсцисс. На малых частотах намотка по-прежнему группируется в правой полуплоскости.

Как только мы убираем сдвиг, т. е. берём сигнал вида g(t) = cos (6πt), намотка при низких частотах сдвигается влево по оси абсцисс.

Построение радиус-вектора остаётся аналогичным. Его длина равна модулю значения сигнала, направление вращения – положительное. Но при смене знака g(t) направление вектора меняется на противоположное.

Сейчас вы увидите, как меняется намотка и х-координата центра масс несмещённого сигнала.

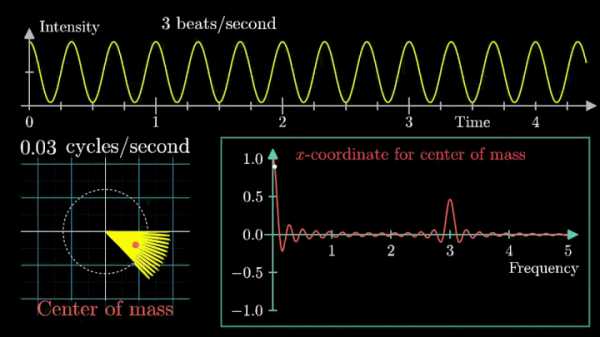
Таким образом, на графике остался только один резкий скачок.

Это важный момент при использовании преобразования Фурье: линейный тренд и смещение проявляются на низких частотах, потому их исключают из исходного сигнала.

4. Выделяем частоты полигармонического сигнала

Теперь рассмотрим сумму двух гармонических сигналов с частотой колебаний f₁ = 2 с^-1 и f₂ = 3 с^-1. Проделаем с ней те же операции – «намотаем» возле начала координат, и, меняя частоту вращения, построим график х-координаты центра масс.

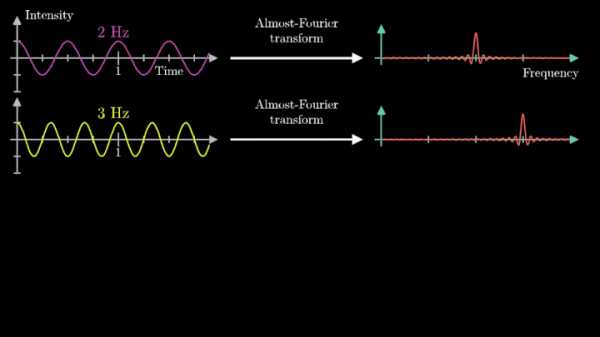
Мы наблюдаем два пика в точках f_В = 2 об/с и f_В = 3 об/с, что соответствует частотному составу исходной суммы.

Отметим ещё один интересный факт, верный как для х-координаты, так и для преобразования Фурье. Преобразование для суммы сигналов и сумма преобразований сигналов имеют один и тот же вид. Т. е. преобразование Фурье линейно.

Таким образом, этот подход позволяет определить частоту колебаний как моно-, так и полигармонического сигнала. Осталось математически описать процедуру вычисления центра масс намотки.

Вывод преобразования Фурье

В самом начале рассмотрения мы отобразили исходный сигнал на комплексную плоскость. Такой выбор не случаен – это позволяет рассматривать точки на плоскости как комплексные числа и использовать формулу Эйлера для описания намотки:

e^iφ=cos(φ)+i·sin(φ).

Геометрически это соотношение означает, что при любом φ точка e^iφ на комплексной плоскости лежит на единичной окружности.

Построим радиус-вектор e^iφ при разных значениях φ.

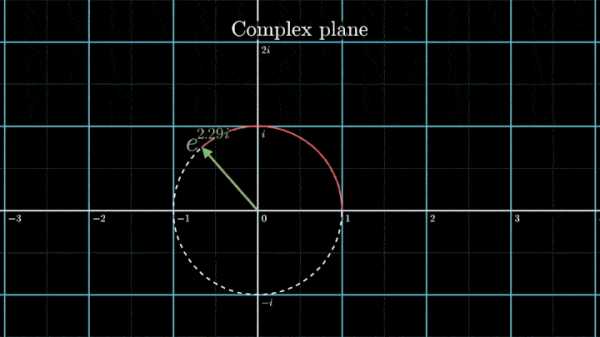
При изменении φ на 2π вектор проходит полный оборот против часовой стрелки, так как 2π – длина единичной окружности. Чтобы задать скорость вращения вектора, показатель степени домножаем на ft, а для смены направления вращения – на -1.

Тогда намотка сигнала g(t) описывается как g(t)e^-2πift.

Теперь вычисляем центр масс. Для этого отметим N произвольных точек на графике намотки и вычислим среднее:

Если мы будем увеличивать количество рассматриваемых точек, придём к предельному случаю:

где t₁ и t₂ – границы интервала, на котором рассматривается сигнал.

Выражение перед интегралом представляет собой масштабирующий коэффициент, но не отражает поведение центра масс. Потому его можно отбросить.

Полученное выражение и будет являться преобразованием Фурье с той разницей, что в общем виде интегрирование задаётся на интервале от -∞ до +∞.

Такой переход к бесконечному интервалу означает, что мы не накладываем никаких ограничений на длительность рассматриваемого сигнала.

Применение преобразования Фурье для фильтрации

Теперь, говоря о преобразовании Фурье, вы можете представлять его геометрическую интерпретацию – намотку сигнала на комплексную плоскость и вычисление центр масс.

При этом частота намотки f становится входным параметром для изображения по Фурье. Центр масс выступает оценкой, насколько хорошо соотносится (коррелирует) параметр f с присутствующими в сигнале частотами.

После того, как вы найдёте в принесённой другом записи все частотные компоненты, вам останется только вычесть их из изображения и применить обратное преобразование Фурье.

Мы что-то упустили? Напишите об этом в комментариях :)

Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих

1. Преобразование Фурье и спектр сигнала

Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который утянул из инета написал программку, уверяет, что она делает преобразование Фурье).

Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:

рис.1 График временной функции сигнала

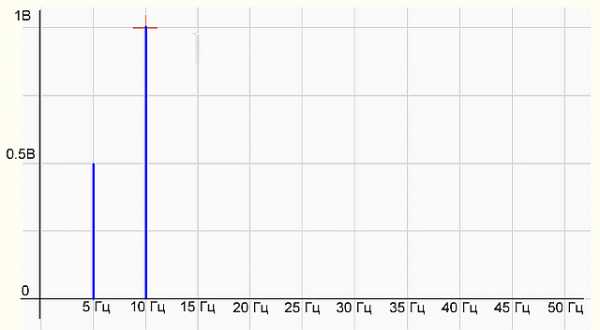
рис.2 График спектра сигнала

На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.

Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.

Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.

С математической точки зрения — сколько ошибок в этой фразе?

Теперь начальство решило мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.


рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек

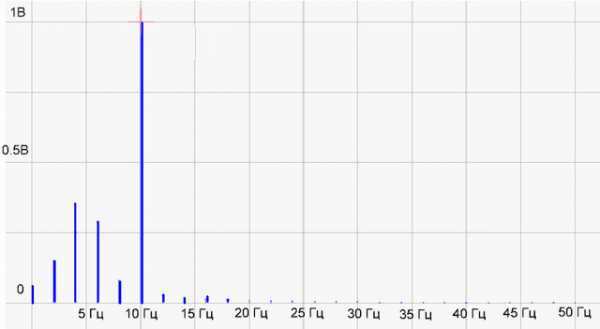
рис.4 Спектр функции

Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…

Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.

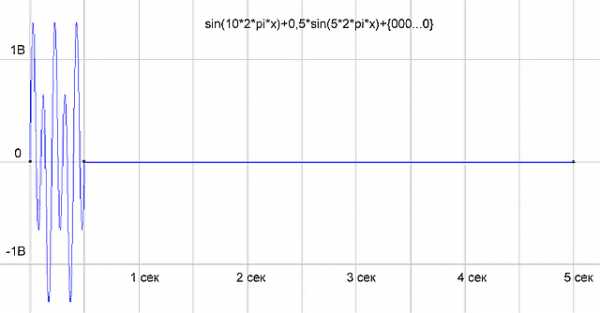
рис.5 Добили нулей до 5 сек

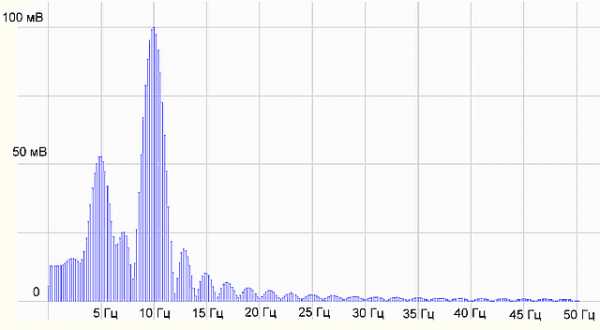
рис.6 Получили спектр

Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.

2. Непрерывная функция и представление её рядом Фурье

Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:

(1), где:

k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей

Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.

(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)

Этот ряд может быть также записан в виде:

(2),
где , k-я комплексная амплитуда.

или

(3)

Связь между коэффициентами (1) и (3) выражается следующими формулами:

и

Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»

Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.

Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид и\или косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.

Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.

Например, на графике рис.7 исходная функция определена на отрезке {-T\2, +T\2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.

Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.

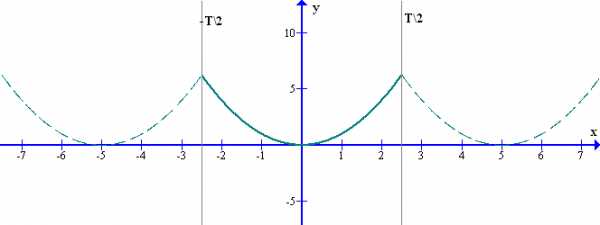
рис.7 Представление непериодической исходной функции рядом Фурье

Таким образом:

Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.

Далее.

Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).

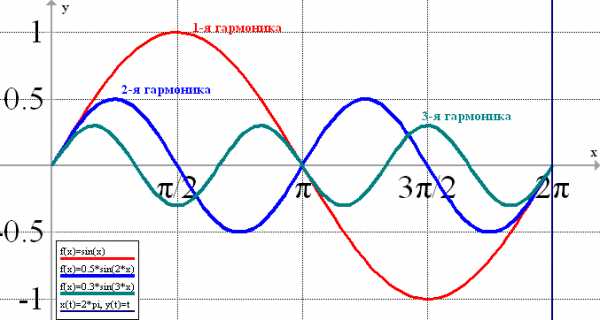
рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)

Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= к\Т, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1\T; к=2 F2=2\T; к=3 F3=3\T;… Fk= к\Т (при нулевой частоте — постоянная составляющая).

Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.

Шаг между гармониками в этом случае равен 1 Гц.

Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.

Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.

3. Дискретные сигналы и дискретное преобразование Фурье

С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).

Обычная схема измерения и оцифровки сигнала выглядит следующим образом.

рис.9 Схема измерительного канала

Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.

рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т

Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).

Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))

Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени , т.е. с частотой Fd ≥ 2*Fмакс, где Fd — частота дискретизации; Fмакс — максимальная частота спектра сигнала. Другими слова частота оцифровки сигнала (частота дискретизации АЦП) должна как минимум в 2 раза превышать максимальную частоту сигнала, который мы хотим измерить.

А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?

В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.

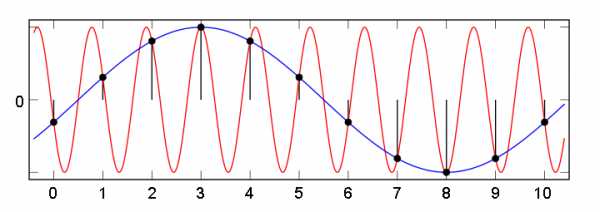
Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации

Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.

Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.

Рассмотрим теперь дискретное преобразование Фурье (ДПФ).

Сравнивая с рядом Фурье

видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.

Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»

Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).

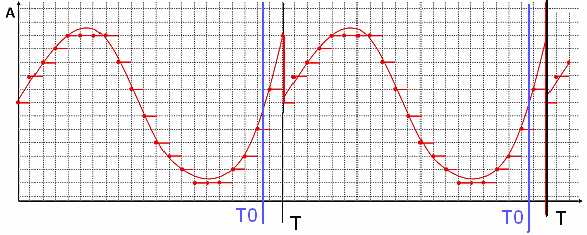
рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0

Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.

Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.

В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.

Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.

Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора

При меньшей длительности картина будет выглядеть «хуже»:

Рис.14 Пример функции и спектра сигнала вибрации ротора

На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.

Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.

Некоторые итоги

1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).

2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».

3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.

Использованные материалы и другие полезные материалы.

FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)

Преобразование Фурье

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Страница проекта на GitHub.

Содержание

Свойство линейности Свойство временного сдвига Преобразование Фурье свертки сигналов Преобразование Фурье произведения сигналов Масштабирование и инверсия во времени Преобразование Фурье производной исходного сигнала Свойство интегрирования исходного сигнала Преобразование Фурье комплексно-сопряженного сигнала Амплитудно- и фазочастотная характеристики сигнала Двойственность преобразования Фурье Убывание спектральной плотности сигнала по частоте Список литературы

Свойство линейности

Пусть даны непериодические сигналы и , а также их спектральные плотности и соответственно. Везде далее мы будем предполагать, что и  — абсолютно интегрируемые сигналы, тогда преобразование Фурье сигнала равно

(1)

Следствием является свойство умножения на константу :

(2)

Свойство временного сдвига

Рассмотрим сигнал как результат временного сдвига исходного сигнала на произвольную величину . Тогда преобразование Фурье сигнала имеет вид:

(3)

Введем замену переменной , тогда и . При любом конечном пределы интегрирования не меняются и спектральная плотность равна:

(4)

Таким образом, задержка сигнала во времени приводит к изменению фазы его спектральной плотности без изменения амплитуды.

Преобразование Фурье свертки сигналов

Пусть сигнал представляет собой свертку сигналов и :

(5)

Тогда спектральная плотность сигнала равна:

(6)

Поменяем порядок интегрирования, и используем свойство (4) временного сдвига:

(7)

Таким образом, спектральная плотность свертки двух сигналов равна произведению их спектральных плотностей.

Это одно из важнейших свойств спектрального анализа, которое позволяет анализировать системы обработки в частотной области, заменяя трудоемкое вычисление свертки сигналов произведением их спектральных плотностей.

Преобразование Фурье произведения сигналов

Пусть сигнал представляет собой произведение сигналов и . Преобразование Фурье сигнала равно:

(8)

Подставим в (8) вместо сигнала обратное преобразование Фурье его спектральной плотности :

(9)

Поменяем в (9) операции интегрирования и получим:

(10)

Тогда окончательно преобразование Фурье произведения сигналов

(11)

пропорционально свертке спектральных плотностей этих сигналов.

Масштабирование и инверсия во времени

Пусть сигнал представляет собой масштабированный во времени сигнал ,  — вещественная константа, отличная от нуля.

Тогда преобразование Фурье сигнала равно:

(12)

Введем в выражении (12) замену переменной , тогда , . При этом пределы интегрирования при положительном не меняются: , откуда , и аналогично . Тогда (12) принимает вид:

(13)

При отрицательном , помимо масштабирования имеет место инверсия сигнала во времени. Тогда вводя замену переменной в (12), пределы интегрирования при также меняются: , , и аналогично , откуда . В результате при получаем:

(14)

Знак минус в выражении (14) появился в результате перестановки нижнего и верхнего пределов интегрирования. Объединяя выражения (13) и (14), для любого вещественного можно записать:

(15)

Следствием (15) является свойство преобразования Фурье инверсного во времени сигнала при :

(16)

Временна́я инверсия сигнала приводит к частотной инверсии его спектральной плотности.

Преобразование Фурье производной исходного сигнала

Пусть сигнал представляет собой непрерывный на всей числовой оси абсолютно интегрируемый сигнал, чья спектральная плотность равна . Тогда сигнал также является абсолютно интегрируемым, и его преобразование Фурье равно:

(17)

Используем правило интегрирования по частям [2, стр. 330]:

(18)

Учтем, что модуль комплексной экспоненты равен единице, а сигнал является абсолютно интегрируемым, т.е. . Тогда два первых слагаемых выражения (18) равны нулю, и окончательно можно записать:

(19)

Таким образом, спектральная плотность производной сигнала равна спектральной плотности этого сигнала, умноженной на .

Как и в случае с периодическими сигналами, наличие множителя приводит к тому, что с ростом частоты затухает слабее чем спектральная плотность исходного сигнала . Поэтому изначально мы наложили ограничение на исходный сигнал: он должен быть непрерывным, тогда его спектральная плотность будет затухать быстрее чем , и умножение на не приведет к росту с увеличением частоты, т.е. обеспечит сходимость (17).

Свойство интегрирования исходного сигнала

Пусть теперь представляет собой сигнал с нулевой постоянной составляющей. Спектральная плотность сигнала равна нулю при .

Тогда сигнал

(20)

представляет собой выход интегратора при входном сигнале .

Обратим внимание, что при , сигнал  является абсолютно интегрируемым.

Рассмотрим спектральную плотность сигнала . Для этого заметим, что сигнал ничто иное, как производная сигнала . Тогда используя свойство преобразования Фурье производной сигнала (19) можно записать:

(21)

При , спектральная плотность рассчитывается без особого труда. Однако на частоте получаем неопределенность вида , раскрытие которой по правилу Лопиталя [2, стр. 257] по аналогии со свойством ряда Фурье приводит к окончательному выражению вида:

(22)

Анализируя (22) можно заключить, что интегрирование сигнала устраняет разрывы и приводит к более быстрому затуханию спектральной плотности, ввиду наличия дополнительного множителя .

Преобразование Фурье комплексно-сопряженного сигнала

Пусть исходный сигнал представляет собой комплексный абсолютно интегрируемый сигнал, где  — синфазная и  — квадратурная компоненты. Рассмотрим преобразование Фурье , используя формулу Эйлера представления комплексных экспонент:

(23)

где , , и  — соответствующее значение каждого из четырех интегралов. Заметим, что справедливы следующие равенства:

(24)

Рассмотрим теперь преобразование Фурье комплексно-сопряженного сигнала :

(25)

Учтем свойство (24), тогда:

(26)

и сравнивая с (23) можно заключить, что:

(27)

Таким образом, спектральная плотность комплексно-сопряженного сигнала равна инверсной по частоте комплексно-сопряженной спектральной плотности исходного сигнала.

Важным следствием (27) является свойство симметрии спектральной плотности вещественного сигнала.

Пусть имеется вещественный сигнал , чья спектральная плотность равна . Поскольку сигнал вещественный, то комплексное сопряжение его не меняет, т.е. . Перейдя в частотную область, с учетом (27) получаем равенство:

(28)

Таким образом, спектральная плотность вещественного сигнала обладает симметрией относительно нулевой частоты.

Для вещественного сигнала выражение (24) с учетом можно представить:

(29)

и спектральная плотность (23) вещественного сигнала принимает вид:

(30)

Тогда определяет реальную часть спектральной плотности и является четной функцией частоты, а  — мнимая часть спектральной плотности является нечетной функцией частоты.

Амплитудно- и фазочастотная характеристики сигнала

По аналогии с понятиями амплитудного и фазового спектра периодического сигнала можно ввести понятия амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристики сигнала:

(31)

Тогда, в случае вещественного сигнала, с учетом свойств симметрии спектральной плотности (28), можно заключить, что АЧХ является четной функцией частоты , а ФЧХ — нечетной: .

Свойство симметрии наглядно показано на рисунке 1 для одностороннего экспоненциального импульса.

Рисунок 1. Симметрия АЧХ и ФЧХ экспоненциального импульса:
а — сигнал во времени; б — АЧХ (сплошная) и ФЧХ (пунктирная)

Двойственность преобразования Фурье

Пусть сигнал имеет спектральную плотность . Рассмотрим что произойдет, если мы возьмем преобразование Фурье от спектральной плотности :

(32)

Обратите внимание, интегрирование идет по переменной , хотя выражение (32) представляет собой прямое преобразование Фурье. Тогда можно переписать:

(33)

Можно сделать вывод, что преобразование Фурье от спектральной плотности снова возвращает сигнал, инверсный во времени, умноженный на . Это свойство носит название двойственности (дуальности) преобразования Фурье.

Двойственность преобразования Фурье позволяет формулировать свойства как для временного так и для частотного представления одновременно. Внимательный читатель уже мог отметить схожесть формулировок свойств преобразования Фурье. Так свертка сигналов во времени приводит к произведению спектральных плотностей, в то время как произведение сигналов во времени приводит к свертке в частотной области. Таким образом, свойство остается справедливым если в формулировке данного свойства поменять местами время и частоту.

При рассмотрении свойства временного сдвига мы получили, что спектральная плотность умножается на комплексную экспоненту. Тогда руководствуясь двойственностью преобразования Фурье можно предположить, что сдвиг спектральной плотности по частоте приведет к умножению сигнала на комплексную экспоненту во времени. Действительно, обратное преобразование от спектральной плотности смещенной по частоте на величину , равно:

(34)

Вводя замену переменной получаем , . Пределы интегрирования остаются неизменными, и выражение (34) принимает вид:

(35)

Как мы и предполагали, смещение спектральной плотности по частоте приводит к умножению сигнала на комплексную экспоненту.

Обратим внимание, что при смещении спектральной плотности вещественного сигнала по частоте, мы нарушаем симметрию , и сигнал после умножения на комплексную экспоненту становится комплексным.

Продолжая рассмотрение двойственности преобразования Фурье, мы можем легко сформулировать требования к сигналу, при котором его спектральная плотность будет вещественной.

Мы говорили, что спектральная плотность вещественного сигнала  является симметричной относительно нулевой частоты: . Тогда мы можем переформулировать это свойство и в другую сторону: если сигнал (в общем случае комплексный) обладает свойством симметрии во временной области: , то его спектральная плотность чисто вещественна.

Для доказательства данного утверждения представим сигнал в виде . Тогда . Если выполняется условие симметрии , то:

(36)

Тогда с учетом выражения (23) и (24), мнимая часть спектральной плотности равна:

(37)

где

(38)

Заметим, что (38) представляет собой интегралы в бесконечных симметричных пределах от произведения четной и нечетной функции (четность и нечетность мы установили выше). Тогда можно заключить, что оба интеграла (38) равны нулю, и мнимая часть спектральной плотности , симметричного во времени сигнала , также равна нулю согласно (37). Что и требовалось доказать.

Убывание спектральной плотности сигнала по частоте

Мы уже отмечали тот факт, что дифференцирование сигнала приводит к умножению спектральной плотности на , т.е. спектральная плотность производной сигнала убывает медленнее с ростом частоты, чем спектральная плотность исходного сигнала. При интегрировании сигнала  — наоборот, спектральная плотность делится на и убывает быстрее исходного сигнала.

Таким образом, можно предположить, что скорость убывания спектральной плотности зависит от степени гладкости исходного сигнала  и наша цель установить данную зависимость.

Прежде всего, нам потребуется обратиться к лемме Римана-Лебега.

Лемма (Римана-Лебега). Преобразование Фурье абсолютно-интегрируемой функции является ограниченной функцией частоты , при этом стремится к нулю при .

Доказательство данной леммы приведено в [3, стр. 83–84]. Лемма Римана-Лебега доказывает качественное свойство убывания спектральной плотности абсолютно-интегрируемого сигнала с ростом частоты , но не дает количественной оценки скорости убывания .

Пусть исходный сигнал является непрерывной, абсолютно-интегрируемой функцией времени, которая может быть дифференцируема  раз, причем все  первых производных также будут представлять собой абсолютно-интегрируемые функции. Тогда производную порядка сигнала можно обозначить как . Если все первых производных являются абсолютно-интегрируемыми, то мы можем перейти в частотную область и согласно свойству преобразования Фурье, спектральная плотность равна:

(39)

откуда . Таким образом, можно заключить, что спектральная плотность убывает быстрее чем , если сигнал может быть раз дифференцируем.

Если сигнал является бесконечно дифференцируемым, например гауссов импульс , то скорость убывания его спектральной плотности носит экспоненциальный характер, что выше любой конечной степени .

Наличие в сигнале разрыва первого рода (например скачка в прямоугольном импульсе) приводит к убыванию спектральной плотности со скоростью с ростом частоты.

Выводы

В данном разделе мы рассмотрели некоторые свойства преобразования Фурье.

В следующем разделе мы рассмотрим спектральные плотности некоторых распространенных сигналов.

Смотри также

Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Преобразование Фурье непериодических сигналов
Спектральные плотности некоторых сигналов
Информация была полезна? Поделитесь с друзьями!

Примечания

Преобразование Фурье представляет собой интеграл в бесконечных пределах. Применение правила интегрирования по частям возможно [1, стр. 374] при соблюдении условия сходимости выражения (17), которое обеспечивается при непрерывном .

Список литературы

[1] Будак, Б.М., Фомин, С.В. Кратные интегралы и ряды. Москва, Наука, 1965, 608 c.

[2] Ильин, В.А., Позняк Э.Г. Основы математического анализа. Москва, Наука, 1965, 572 c.

[3] Хургин, Я.И., Яковлев, В.П. Финитные функции в физике и технике. Москва, Наука, 1971, 408 с.

[4] Баскаков, С.И. Радиотехнические цепи и сигналы Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[5] Гоноровский И.С. Радиотехнические цепи и сигналы Москва, Советское радио, 1977, 608 c.

[6] Bracewell, R. The Fourier Transform and Its Applications McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

© Бахурин Сергей 2015 - 2020. Все права защищены. Любое копирование материалов сайта без разрешения автора запрещено.

Фурье преобразование - это... Что такое Фурье преобразование?

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Преобразование Фурье функции f вещественной переменной является интегральным преобразованием и задается следующей формулой:

Отметим, что разные источники могут давать определения, отличающиеся от приведенного выбором коэффициента перед интегралом, а также знака «-» в показателе экспоненты. Все свойства в этом случае будут аналогичны, хотя вид каких-то формул может измениться.

Кроме этого, существуют разнообразные обобщения этого понятия, которые будут приведены ниже.

Определения, основные свойства

Хотя формула, задающая преобразование Фурье, имеет ясный смысл только для функций класса , преобразование Фурье может быть определено и для более широкого класса функций, и даже обобщённых функций. Это возможно благодаря ряду свойств преобразования Фурье:

Это свойство позволяет по непрерывности распространить определение преобразования Фурье на всё пространство . Равенство Парсеваля будет при этом справедливо для всех .

• Формула обращения:

справедлива, если интеграл в правой части имеет смысл. В частности, это верно, если функция f является достаточно гладкой. Если , то формула также верна, поскольку равенство Парсеваля позволяет придать интегралу в правой части смысл с помощью предельного перехода.

Эта формула объясняет физический смысл преобразования Фурье: правая часть — (бесконечная) сумма гармонических колебаний e^iωx с частотами ω, амплитудами и фазовыми сдвигами argf(ω) соответственно.

• Теорема о свертке: если , тогда

, где

Эта формула может быть распространена и на случай обобщённых функций.

• Преобразование Фурье и дифференцирование. Если , то

Из этой формулы легко выводится формула для n-й производной:

Формулы верны и в случае обобщённых функций.

• Преобразование Фурье и сдвиг.

Эта и предыдущая формула являются частными случаями теоремы о свёртке, так как сдвиг по аргументу — это свёртка со сдвинутой дельта-функций δ(x − x₀), а дифференцирование — свёртка с производной дельта-функции.

• Преобразование Фурье и растяжение.

• Преобразование Фурье обобщённых функций. Преобразование Фурье можно определить для широкого класса обобщённых функций. Определим вначале пространство гладких быстро убывающих функций (пространство Шварца):

Ключевым свойством этого пространства является то, что это инвариантное подпространство по отношению к преобразованию Фурье.

Теперь определим его двойственное пространство . Это некоторое подпространство в пространстве всех обобщённых функций — так называемые обобщённые функции медленного роста. Теперь для функции её преобразованием Фурье называется обобщённая функция , действующая на основные функции по правилу

Например, вычислим преобразование Фурье дельта-функции:

Таким образом, преобразованием Фурье дельта-функции является константа .

Применения преобразования Фурье

Преобразование Фурье используется во многих областях науки — в физике, теории чисел, комбинаторике, обработке сигналов, теории вероятностей, статистике, криптографии, акустике, океанологии, оптике, геометрии, и многих других. В обработке сигналов и связанных областях преобразование Фурье обычно рассматривается как декомпозиция сигнала на частоты и амплитуды, то есть, обратимый переход от временно́го пространства (time domain) в частотное пространство (frequency domain). Богатые возможности применения основываются на нескольких полезных свойствах преобразования:

• Преобразования являются линейными операторами и, с соответствующей нормализацией, также являются унитарными (свойство, известное как теорема Парсеваля или, в более общем случае как теорема Планшереля, или в наиболее общем как дуализм Понтрягина).
• Преобразования обратимы, причём обратное преобразование имеет практически такую же форму, как и прямое преобразование.
• Синусоидальные базисные функции являются собственными функциями дифференцирования, что означает, что данное представление превращает линейные дифференциальные уравнения с постоянными коэффициентами в обычные алгебраические. (Например, в линейной стационарной системе частота — консервативная величина, поэтому поведение на каждой частоте может решаться независимо.)
• По теореме о свёртке, преобразование Фурье превращает сложную операцию свёртки в простое умножение, что означает, что они обеспечивают эффективный способ вычисления основанных на свёртке операций, таких как умножение многочленов и умножение больших чисел.
• Дискретная версия преобразования Фурье может быстро рассчитываться на компьютерах, используя алгоритм быстрого преобразования Фурье (БПФ, англ. FFT).

Разновидности преобразования Фурье

Многомерное преобразование Фурье

Преобразование Фурье функций, заданных на пространстве , определяется формулой

Здесь ω и x — векторы пространства ,  — их скалярное произведение. Обратное преобразование в этом случае задается формулой

Эта формула может быть интерпретирована как разложение функции f в линейную комбинацию (суперпозицию) «плоских волн» вида с амплитудами , частотами ω и фазовыми сдвигами соответственно. Как и прежде, в разных источниках определения многомерного преобразования Фурье могут отличаться выбором константы перед интегралом.

Замечание относительно области задания преобразования Фурье и его основные свойства остаются справедливыми и в многомерном случае, со следующими уточнениями:

• Взятие частных производных под действием преобразования Фурье превращается в умножение на одноимённую координату:

• Изменяется константа в теореме о свёртке:

• Преобразование Фурье и сжатие координат:

Ряды Фурье

Непрерывное преобразование само фактически является обобщением более ранней идеи рядов Фурье, которые определены для 2π-периодических функций и представляют собой разложение таких функций в (бесконечную) линейную комбинацию гармонических колебаний с целыми частотами:

Разложение в ряд Фурье применимо также к функциям, заданным на ограниченных промежутках, поскольку такие функции могут быть периодически продолжены на всю прямую.

Ряд Фурье является частным случаем преобразования Фурье, если последнее понимать в смысле обобщённых функций. Для любой 2π-периодической функции имеем

Иными словами, преобразование Фурье периодической функции представляет собой сумму точечных нагрузок в целых точках, и равно нулю вне их.

Дискретное преобразование Фурье

Дискретное преобразование Фурье — преобразование конечных последовательностей (комплексных) чисел, которое, как и в непрерывном случае, превращает свёртку в поточечное умножение. Используется в цифровой обработке сигналов и в других ситуациях, где необходимо быстро выполнять свёртку, например, при умножении больших чисел.

Пусть  — последовательность комплексных чисел. Рассмотрим многочлен . Выберем какие-нибудь n точек на комплексной плоскости . Теперь многочлену f(t) мы можем сопоставить новый набор из n чисел: . Заметим, что это преобразование обратимо: для любого набора чисел существует единственный многочлен f(t) степени не выше n − 1 с такими значениями в соответственно(см. Интерполяция).

Набор {f_k} и называется дискретным преобразованием Фурье исходного набора {x_k}. В качестве точек z_k обычно выбирают корни n-й степени из единицы:

.

Такой выбор продиктован тем, что в этом случае обратное преобразование принимает простую форму, а также тем, что вычисление преобразования Фурье может быть выполнено особенно быстро. Так, в то время как вычисление свёртки двух последовательностей длины n напрямую требует порядка n² операций, переход к их преобразованию Фурье и обратно по быстрому алгоритму может быть выполнен за O(nlogn) операций. Для преобразований Фурье свёртке соответствует покомпонентное умножение, которое требует лишь порядка n операций.

Оконное преобразование Фурье

где даёт (вообще говоря несколько искажённое) распределение частот части оригинального сигнала f(t) в окрестности времени t.

Классическое преобразование Фурье имеет дело со спектром сигнала, взятым во всем диапазоне существования переменной. Нередко интерес представляет только локальное распределение частот, в то время как требуется сохранить изначальную переменную (обычно время). В этом случае используется обобщение преобразования Фурье, так называемое оконное преобразование Фурье. Для начала необходимо выбрать некоторую оконную функцию W, эта функция должна иметь хорошо локализованный спектр.

Другие варианты

Дискретное преобразование Фурье является частным случаем (и иногда применяется для аппроксимации) дискретного во времени преобразования Фурье (DTFT), в котором x_k определены на дискретных, но бесконечных областях, и таким образом спектр является непрерывным и периодическим. Дискретное во времени преобразование Фурье является по существу обратным для рядов Фурье.

Эти разновидности преобразования Фурье могут быть обобщены на преобразования Фурье произвольных локально сжатых абелевых топологических групп, которые изучаются в гармоническом анализе; они преобразуют группу в ее дуальную группу. Эта трактовка также позволяет сформулировать теорему свёртки, которая устанавливает связь между преобразованиями Фурье и свёртками. См. также дуализм Понтрягина для обобщённых обоснований преобразования Фурье.

Интерпретация в терминах времени и частоты

В терминах обработки сигналов, преобразование берёт представление функции сигнала в виде временны́х рядов и отображает его в частотный спектр, где ω — угловая частота. То есть оно превращает функцию времени в функцию частоты; это разложение функции на гармонические составляющие на различных частотах.

Когда функция f является функцией времени и представляет физический сигнал, преобразование имеет стандартную интерпретацию как спектр сигнала. Абсолютная величина получающейся в результате комплексной функции F представляет амплитуды соответствующих частот (ω), в то время как фазовые сдвиги получаются как аргумент этой комплексной функции.

Однако важно осознавать, что преобразования Фурье не ограничиваются функциями времени и временными частотами. Они могут в равной степени применяться для анализа пространственных частот, также как для практически любых других функций.

Таблица важных преобразований Фурье

Следующая таблица содержит список важных формул для преобразования Фурье F(ω) и G(ω) обозначают фурье компоненты функций f(t) и g(t), соответственно. f и g должны быть интегрируемыми функциями или обобщёнными функциями.

Помните, что соотношения в этой таблице и в особенности множители такие как , зависят от соглашения, какая форма определения для Фурье преобразования использовалась прежде (хотя в общем виде соотношения, конечно, правильны).

Литература

• Сергиенко А. Б. Цифровая обработка сигналов. — 2-е. — Спб: Питер, 2006. — С. 751. — ISBN 5-469-00816-9

• М. А. Павлейно, В. М. Ромаданов Спектральные преобразования в MatLab. — СПб: 2007. — С. 160. — ISBN 978-5-98340-121-1

См. также

Ссылки

Wikimedia Foundation. 2010.

Оконное преобразование Фурье — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 сентября 2018; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 сентября 2018; проверки требуют 3 правки.

Оконное преобразование Фурье — это разновидность преобразования Фурье, определяемая следующим образом:

F(t,ω)=∫−∞∞f(τ)W(τ−t)e−iωτdτ,{\displaystyle F(t,\omega )=\int \limits _{-\infty }^{\infty }f(\tau )W(\tau -t)e^{-i\omega \tau }\,d\tau ,}

где W(τ−t){\displaystyle W(\tau -t)} — некоторая оконная функция. В случае дискретного преобразования оконная функция используется аналогично:

F(m,ω)=∑n=−∞∞f[n]w[n−m]e−jωn{\displaystyle F(m,\omega )=\sum _{n=-\infty }^{\infty }f[n]w[n-m]e^{-j\omega n}}

Существует множество математических формул, визуально улучшающих частотный спектр на разрыве границ окна. Для этого применяются преобразования: треугольное (Барлетта), синус-окно, синус в кубе, синус в 4-й степени, преобразование Парзена, Уэлча, Гаусса, Хеннинга, приподнятый косинус (Хэмминга), Чебышева, с пульсациями, Розенфилда, Блэкмана-Харриса, горизонтальное и с плоской вершиной. Также существует методика по взаимному перекрытию окон, при этом обычно можно выбрать сколько семплов из предыдущего окна будет усреднено с текущим окном.

На практике нет возможности получить сигнал на бесконечном интервале, так как нет возможности узнать, какой был сигнал до включения устройства и какой он будет в будущем. Ограничение интервала анализа равносильно произведению исходного сигнала на прямоугольную оконную функцию. Таким образом, результатом оконного преобразования Фурье является не спектр исходного сигнала, а спектр произведения сигнала и оконной функции. В результате возникает эффект, называемый растеканием спектра сигнала. Опасность заключается в том, что боковые лепестки^{[уточнить]} сигнала более высокой амплитуды могут маскировать присутствие других сигналов меньшей амплитуды.

Для борьбы с растеканием спектра применяют более гладкую оконную функцию, спектр которой имеет более широкий главный лепесток и низкий уровень боковых лепестков. Спектр, полученный при помощи оконного преобразования Фурье, является сверткой спектра исходного идеального сигнала и спектра оконной функции.

Искажения, вносимые применением окон, определяются размером окна и его формой. Выделяют следующие основные свойства оконных функций: ширина главного лепестка по уровню -3 дБ, ширина главного лепестка по нулевому уровню, максимальный уровень боковых лепестков, коэффициент ослабления оконной функции.

При использовании оконного преобразования Фурье невозможно одновременно обеспечить хорошее разрешение по времени и по частоте. Чем уже окно, тем выше разрешение по времени и ниже разрешение по частоте.

Сравнение оконного преобразования Фурье с разными окнами. Слева (узкое окно) - хорошее разрешение по времени, справа (более широкое окно) - хорошее разрешение по частоте.

Разрешение по осям является постоянным. Это нежелательно для ряда задач, в которых информация по частотам распределена неравномерно. В таких задачах в качестве альтернативы оконному преобразованию Фурье может использоваться вейвлет-преобразование, временное разрешение которого увеличивается с частотой (частотное снижается).

Прямоугольное окно[править | править код]

Прямоугольное окно; B=1.00

w(n)={1,n∈[0,N−1]0,n∉[0,N−1]{\displaystyle w(n)=\left\{{\begin{matrix}1,&n\in [0,N-1]\\0,&n\notin [0,N-1]\\\end{matrix}}\right.}

Получается автоматически при ограничении выборки N отсчетами. Максимальный уровень боковых лепестков частотной характеристики: -13 дБ.

Окно Ханна (Хеннинга)[править | править код]

Окно Ханна; B = 1.50

w(n)=0.5(1−cos⁡(2πnN−1)){\displaystyle w(n)=0.5\;\left(1-\cos \left({\frac {2\pi n}{N-1}}\right)\right)}

где N — ширина окна. Уровень боковых лепестков: -31.5 дБ.

Окно Хэмминга[править | править код]

Окно Хэмминга

w(n)=0.53836−0.46164cos⁡(2πnN−1){\displaystyle w(n)=0.53836-0.46164\;\cos \left({\frac {2\pi n}{N-1}}\right)}

Уровень боковых лепестков: -42 дБ.

Окно Блэкмана[править | править код]

Окно Блэкмана; α = 0.16; B=1.73

w(n)=a0−a1cos⁡(2πnN−1)+a2cos⁡(4πnN−1){\displaystyle w(n)=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N-1}}\right)+a_{2}\cos \left({\frac {4\pi n}{N-1}}\right)}

a0=1−α2;a1=12;a2=α2{\displaystyle a_{0}={\frac {1-\alpha }{2}};\quad a_{1}={\frac {1}{2}};\quad a_{2}={\frac {\alpha }{2}}}

Уровень боковых лепестков: -58 дБ (α=0.16).

Окно Кайзера[править | править код]

Окно Кайзера, α =2; B=1.5 Окно Кайзера, α =3; B=1.8

w(n)=|I0(β1−(2n−N+1N−1)2)||I0(β)|{\displaystyle w(n)={\frac {|I_{0}\left(\beta {\sqrt {1-\left({\frac {2n-N+1}{N-1}}\right)^{2}}}\right)|}{|I_{0}(\beta )|}}}

где I0{\displaystyle I_{0}} — модифицированная функция Бесселя первого рода нулевого порядка; β{\displaystyle \beta } — коэффициент определяющий долю энергии, сосредоточенной в главном лепестке спектра оконной функции. Чем больше β{\displaystyle \beta } тем больше доля энергии, и шире главный лепесток, и меньше уровень боковых лепестков. На практике используются значения от 4 до 9.

Понимание алгоритма БПФ / OTUS. Онлайн-образование corporate blog / Habr

Здравствуйте, друзья. Уже завтра стартует курс «Алгоритмы для разработчиков», а у нас остался один неопубликованный перевод. Собственно исправляемся и делимся с вами материалом. Поехали.

Быстрое преобразование Фурье (БПФ — англ. FFT) является одним из важнейших алгоритмов обработки сигналов и анализа данных. Я пользовался им годами, не имея формальных знаний в области компьютерных наук. Но на этой неделе мне пришло в голову, что я никогда не задавался вопросом, как БПФ так быстро вычисляет дискретное преобразование Фурье. Я стряхнул пыль со старой книги по алгоритмам, открыл ее, и с удовольствием прочитал об обманчиво простой вычислительной уловке, которую Дж. В. Кули и Джон Тьюки описали в своей классической работе 1965 года, посвященной этой теме.

Цель этого поста — окунуться в алгоритм БПФ Кули-Тьюки, объясняя симметрии, которые к нему приводят, и показать несколько простых реализаций на Python, применяющих теорию на практике. Я надеюсь, что это исследование даст специалистам по анализу данных, таким как я, более полную картину того, что происходит под капотом используемых нами алгоритмов.

Дискретное преобразование Фурье

БПФ — это быстрый алгоритм для вычисления дискретного преобразования Фурье (ДПФ), которое напрямую вычисляется за . ДПФ, как и более знакомая непрерывная версия преобразования Фурье, имеет прямую и обратную форму, которые определяются следующим образом:

Прямое дискретное преобразование Фурье (ДПФ):

Обратное дискретное преобразование Фурье (ОДПФ):

Преобразование из xn → Xk является переводом из конфигурационного пространства в пространство частотное и может быть очень полезным как для исследования спектра мощности сигнала, так и для преобразования определенных задач для более эффективного вычисления. Некоторые примеры этого в действии вы можете найти в главе 10 нашей будущей книги по астрономии и статистике, где также можно найти изображения и исходный код на Python. Пример использования БПФ для упрощения интегрирования сложных в противном случае дифференциальных уравнений смотрите в моем посте «Решение уравнения Шредингера в Python».

Из-за важности БПФ (далее может быть использовано равносильное FFT — Fast Fourier Transform) во многих областях Python содержит множество стандартных инструментов и оболочек для его вычисления. И NumPy, и SciPy имеют оболочки из чрезвычайно хорошо протестированной библиотеки FFTPACK, которые находятся в подмодулях numpy.fft и scipy.fftpack соответственно. Самый быстрый БПФ, о котором я знаю, находится в пакете FFTW, который также доступен в Python через пакет PyFFTW.

На данный момент, однако, давайте оставим эти реализации в стороне и зададимся вопросом, как мы можем вычислить БПФ в Python с нуля.

Вычисление дискретного преобразования Фурье

Для простоты мы будем касаться только прямого преобразования, поскольку обратное преобразование может быть реализовано очень похожим образом. Взглянув на приведенное выше выражение ДПФ (DFT), мы видим, что это не более чем прямолинейная линейная операция: умножение матрицы на вектор

с матрицей М, заданной

Имея это в виду, мы можем вычислить ДПФ с использованием простого умножения матрицы следующим образом:

In [1]:

import numpy as np def DFT_slow(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x)

Мы можем перепроверить результат, сравнив его со встроенной в numpy БПФ-функцией:

In [2]:

x = np.random.random(1024) np.allclose(DFT_slow(x), np.fft.fft(x))

0ut[2]:

True

Просто чтобы подтвердить медлительность нашего алгоритма, мы можем сравнить время выполнения этих двух подходов:

In [3]:

%timeit DFT_slow(x) %timeit np.fft.fft(x)

10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop

Мы более чем в 1000 раз медленнее, что и следовало ожидать для такой упрощенной реализации. Но это не самое худшее. Для входного вектора длины N алгоритм БПФ масштабируется как , в то время как наш медленный алгоритм масштабируется как . Это означает, что для элементов мы ожидаем, что БПФ завершится за где-то около 50 мс, в то время как наш медленный алгоритм займет около 20 часов!

Так как же БПФ добивается такого ускорения? Ответ заключается в использовании симметрии.

Симметрии в дискретном преобразовании Фурье

Одним из наиболее важных инструментов в построении алгоритмов является использование симметрий задачи. Если вы можете аналитически показать, что одна часть проблемы просто связана с другой, вы можете вычислить подрезультат только один раз и сэкономить эти вычислительные затраты. Кули и Тьюки использовали именно этот подход при получении БПФ.
Мы начнем с вопроса о значении . Из нашего выражения выше:

где мы использовали тождество exp [2π i n] = 1, которое выполняется для любого целого числа n.

Последняя строка хорошо показывает свойство симметрии ДПФ:

Простым расширением,

для любого целого числа i. Как мы увидим ниже, эту симметрию можно использовать для гораздо более быстрого вычисления ДПФ.

ДПФ в БПФ: использование симметрии

Кули и Тьюки показали, что можно разделить вычисления БПФ на две меньшие части. Из определения ДПФ имеем:

Мы разделили одно дискретное преобразование Фурье на два слагаемых, которые сами по себе очень похожи на меньшие дискретные преобразования Фурье, одно на значения с нечетным номером и одно на значения с четным номером. Однако до сих пор мы не сохранили никаких вычислительных циклов. Каждый член состоит из (N / 2) ∗ N вычислений, всего .

Хитрость заключается в использовании симметрии в каждом из этих условий. Поскольку диапазон k равен 0≤k <N, а диапазон n равен 0≤n <M≡N / 2, мы видим из свойств симметрии выше, что нам нужно выполнить только половину вычислений для каждой подзадачи. Наше вычисление стало , где M в два раза меньше N.

Но причин останавливаться на этом нет: пока наши меньшие преобразования Фурье имеют четное M, мы можем повторно применять этот подход «разделяй и властвуй», каждый раз вдвое уменьшая вычислительные затраты, пока наши массивы не станут достаточно маленькими, чтобы стратегия больше не сулила выгоды. В асимптотическом пределе этот рекурсивный подход масштабируется как O [NlogN].

Этот рекурсивный алгоритм может быть очень быстро реализован на Python, отталкиваясь от нашего медленного ДПФ кода, когда размер подзадачи становится достаточно маленьким:

In [4]:

def FFT(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if N % 2 > 0: raise ValueError("size of x must be a power of 2") elif N <= 32: # this cutoff should be optimized return DFT_slow(x) else: X_even = FFT(x[::2]) X_odd = FFT(x[1::2]) factor = np.exp(-2j * np.pi * np.arange(N) / N) return np.concatenate([X_even + factor[:N / 2] * X_odd, X_even + factor[N / 2:] * X_odd])

Здесь мы сделаем быструю проверку того, что наш алгоритм дает правильный результат:
In [5]:

x = np.random.random(1024) np.allclose(FFT(x), np.fft.fft(x))

Out[5]:
True

Сопоставим этот алгоритм с нашей медленной версией:
-In [6]:

%timeit DFT_slow(x) %timeit FFT(x) %timeit np.fft.fft(x)

10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop

Наш расчет быстрее чем прямая версия на порядок! Более того, наш рекурсивный алгоритм асимптотически : мы реализовали быстрое преобразование Фурье.

Обратите внимание, что мы все еще не приблизились к скорости встроенного алгоритма FFT в numpy, и этого следовало ожидать. Алгоритм FFTPACK, стоящий за fft numpy, — это реализация на Фортране, которая получила годы доработок и оптимизаций. Кроме того, наше решение NumPy включает в себя как рекурсию стека Python, так и выделение множества временных массивов, что увеличивает время вычислений.

Хорошая стратегия для ускорения кода при работе с Python / NumPy — по возможности векторизовать повторяющиеся вычисления. Это мы можем сделать — в процессе удалять наши рекурсивные вызовы функций, что сделает наш Python FFT еще более эффективным.

Векторизованная Numpy-версия

Обратите внимание, что в вышеупомянутой рекурсивной реализации FFT на самом низком уровне рекурсии мы выполняем N / 32 идентичных матрично-векторных произведений. Эффективность нашего алгоритма выиграет, если одновременно вычислить эти матрично-векторные произведения как единое матрично-матричное произведение. На каждом последующем уровне рекурсии мы также выполняем повторяющиеся операции, которые можно векторизовать. NumPy отлично справляется с такой операцией, и мы можем использовать этот факт для создания этой векторизованной версии быстрого преобразования Фурье:

In [7]:

def FFT_vectorized(x): """A vectorized, non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2") # N_min here is equivalent to the stopping condition above, # and should be a power of 2 N_min = min(N, 32) # Perform an O[N^2] DFT on all length-N_min sub-problems at once n = np.arange(N_min) k = n[:, None] M = np.exp(-2j * np.pi * n * k / N_min) X = np.dot(M, x.reshape((N_min, -1))) # build-up each level of the recursive calculation all at once while X.shape[0] < N: X_even = X[:, :X.shape[1] / 2] X_odd = X[:, X.shape[1] / 2:] factor = np.exp(-1j * np.pi * np.arange(X.shape[0]) / X.shape[0])[:, None] X = np.vstack([X_even + factor * X_odd, X_even - factor * X_odd]) return X.ravel()

Хотя алгоритм немного более непрозрачен, это просто перестановка операций, используемых в рекурсивной версии, с одним исключением: мы используем симметрию в вычислении коэффициентов и строим только половину массива. Опять же, мы подтверждаем, что наша функция дает правильный результат:

In [8]:

x = np.random.random(1024) np.allclose(FFT_vectorized(x), np.fft.fft(x))

Out[8]:
True

Поскольку наши алгоритмы становятся намного более эффективными, мы можем использовать больший массив для сравнения времени, оставляя DFT_slow:
In [9]:

x = np.random.random(1024 * 16) %timeit FFT(x) %timeit FFT_vectorized(x) %timeit np.fft.fft(x)

10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop

Мы улучшили нашу реализацию еще на порядок! Сейчас мы находимся на расстоянии примерно в 10 раз от эталона FFTPACK, используя всего пару десятков строк чистого Python + NumPy. Хотя это все еще не соответствует в вычислительном отношении, с точки зрения читаемости версия Python намного превосходит исходный код FFTPACK, который вы можете просмотреть здесь.

Итак, как FFTPACK достигает этого последнего ускорения? Ну, в основном, это просто вопрос детальной бухгалтерии. FFTPACK тратит много времени на повторное использование любых промежуточных вычислений, которые можно использовать повторно. Наша клочковатая версия все еще включает в себя избыток выделения памяти и копирования; на низкоуровневом языке, таком как Fortran, легче контролировать и минимизировать использование памяти. Кроме того, алгоритм Кули-Тьюки можно расширить, чтобы использовать разбиения размером, отличным от 2 (то, что мы здесь реализовали, известно как БПФ Кули-Тьюки радикса по основе 2). Также могут быть использованы другие более сложные алгоритмы БПФ, в том числе принципиально отличные подходы, основанные на сверточных данных (см., Например, алгоритм Блюштейна и алгоритм Рейдера). Комбинация вышеупомянутых расширений и методов может привести к очень быстрым БПФ даже на массивах, размер которых не является степенью двойки.

Хотя функции на чистом Python, вероятно, бесполезны на практике, я надеюсь, что они преподнесли некоторую интуицию в том, что происходит на фоне анализа данных на основе FFT. Как специалисты по данным, мы можем справиться с реализацией «черного ящика» фундаментальных инструментов, созданных нашими более алгоритмически настроенными коллегами, но я твердо убежден, что чем больше у нас понимания о алгоритмах низкого уровня, которые мы применяем к нашим данным, тем лучшими практиками мы будем.

Этот пост был полностью написан в блокноте IPython. Полный блокнот можно скачать здесь или посмотреть статически здесь.

Многие могут заметить, что материал далеко не новый, но, как нам кажется, вполне актуальный. В общем пишите была ли статья полезной. Ждём ваши комментарии.

Анализ Фурье — Википедия

Сигнал струны бас гитары, что играет ноту A («Ля» — 55 Гц). Распределение Фурье временного сигнала звука бас гитары для открытой струны A (55 Гц). Анализ Фурье позволяет выявить колебательные компоненты сигналов и функций.

Анализ Фурье — направление в анализе, изучающее каким образом общие математические функции могут быть представлены либо приближены через сумму более простых тригонометрических функций. Анализ Фурье возник при изучении свойств рядов Фурье, и назван в честь Жозефа Фурье, который показал, что представление функции в виде суммы тригонометрических функций значительно упрощает изучение процесса теплообмена.

Сегодня^{[уточнить]} предметом анализа Фурье является широкий спектр математических задач. В науке и технике, процесс разложения функции на колебательные компоненты часто называют анализом Фурье, хотя оперирования и восстановления функций из таких частей известно как синтез Фурье.

Например, при определении какие именно компоненты частот присутствуют в музыкальной ноте, применяют расчёты преобразования Фурье выбранной музыкальной ноты. После чего можно ресинтезировать тот же звук используя те частотные компоненты, которые обнаружили в анализе Фурье. В математике анализом Фурье часто называют обе эти операции.

Процесс разложения сам по себе называется преобразованием Фурье.

Анализ Фурье имеет много применений в науке — в физике, дифференциальных уравнениях с частными производными, теории чисел, комбинаторике, обработке сигналов, обработке цифровых изображений, теории вероятности, статистике, судебной экспертизе, криптографии, численном анализе, акустике, океанографии, геометрии, структурном анализе белков и других областях.

Такая широкая применимость обусловлена многими полезными свойствами преобразования:

Преобразование является линейным отображением и, при соответствующей нормализации, также унитарным (это свойство известно как теорема Парсеваля или, в более общем случае, как теорема Планшереля, и вообще благодаря понятию двойственности Понтрягина)^[1].

• Преобразование, как правило, является обратимым.
• Показательные функции являются собственными функциями для операции дифференцирования, это значит, что такое представление превращает линейные дифференциальные уравнения с постоянными коэффициентами в обычные алгебраические уравнения (Evans 1998). Таким образом, можно анализировать поведение линейных стационарных систем независимо для каждой частоты.
• Благодаря теореме о свёртке преобразования Фурье превращают сложную операцию свёртки в простое умножение, что означает, что такие преобразования позволяют производить расчёты с операциями на основе свёрток, такими, как умножение многочленов и умножения больших чисел, эффективным способом^[2].
• Дискретная версия преобразования Фурье может быстро рассчитываться компьютерами с использованием алгоритмов быстрого преобразования Фурье (FFT)^[3].

В судебной экспертизе при использовании лабораторных инфракрасных спектрофотометров применяют анализ преобразования Фурье для измерения длины волны света, при которой материал будет поглощать инфракрасный спектр. Метод преобразования Фурье используется для декодирования измеренных сигналов и записи данных о длине волны. А при использовании компьютера такие вычисления используются быстро, поэтому такое компьютерно-управляемое устройство может выдать спектр поглощения инфракрасного излучения за считанные секунды^[4].

Преобразование Фурье также используют для компактного представления сигнала. Например, алгоритм сжатия JPEG использует модификацию преобразования Фурье (дискретного косинусного преобразования) для небольших квадратных фрагментов цифрового изображения. Компоненты Фурье каждого квадрата округляются до меньшей арифметической точности, а незначительными компонентами пренебрегают, поэтому оставшиеся компоненты можно хранить очень компактно. При реконструкции изображения каждый квадрат восстанавливается из сохранившихся приближенных компонентов преобразования Фурье, которые потом обратно превращаются в приближенно восстановленное исходное изображение.

(Непрерывное) преобразование Фурье[править | править код]

Чаще всего, без уточнения, преобразование Фурье обозначает применение к преобразованию непрерывных функций действительного аргумента, результатом которого является непрерывная функция частоты, известная как распределения частоты. Одна функция переходит в другую, а сама операция является обратимой. Когда областью определения входной (начальной) функции есть время (t), а областью определения исходной (финальной) функции является частота, преобразование функции s(t) при частоте f задается следующим образом:

S(f)=∫−∞∞s(t)⋅e−2iπftdt.{\displaystyle S(f)=\int _{-\infty }^{\infty }s(t)\cdot e^{-2i\pi ft}\,dt.}

Расчет этой величины при всех значениях f образует функцию в частотной области. Тогда s(t) можно представить как рекомбинации комплексных экспонент для всех возможных частот:

s(t)=∫−∞∞S(f)⋅e2iπftdf,{\displaystyle s(t)=\int _{-\infty }^{\infty }S(f)\cdot e^{2i\pi ft}\,df,}

что является формулой для обралексное число, S( f ), содержит в себе одновременно амплитуду и фазу частоты f.

Ряд Фурье[править | править код]

Преобразование Фурье периодической функции, s_P(t), с периодом P, становится функцией, которая является гребёнкой Дирака, модулированной последовательностью комплексных коэффициентов:

S[k]=1P∫PsP(t)⋅e−2iπkPtdt{\displaystyle S[k]={\frac {1}{P}}\int _{P}s_{P}(t)\cdot e^{-2i\pi {\frac {k}{P}}t}\,dt}

для всех целых значений k, и где ∫_P является интегралом в области интервала длиной P.

Обратное преобразование, известное как ряд Фурье, является представлением s_P(t) в терминах суммы потенциально бесконечного числа гармонично связанных синусоид или комплексных экспоненциальных функций, каждая из которых имеет амплитуду и фазу, заданная одним из коэффициентов:

sP(t)=∑k=−∞∞S[k]⋅e2iπkPt⟺F∑k=−∞+∞S[k]δ(f−kP).{\displaystyle s_{P}(t)=\sum _{k=-\infty }^{\infty }S[k]\cdot e^{2i\pi {\frac {k}{P}}t}\quad {\stackrel {\displaystyle {\mathcal {F}}}{\Longleftrightarrow }}\quad \sum _{k=-\infty }^{+\infty }S[k]\,\delta \left(f-{\frac {k}{P}}\right).}

Когда s_P(t) задается как периодическая сумма другой функции, s(t):

sP(t)=def∑m=−∞∞s(t−mP),{\displaystyle s_{P}(t)\,{\stackrel {\text{def}}{=}}\,\sum _{m=-\infty }^{\infty }s(t-mP),}

коэффициенты пропорциональны элементам S( f ) для дискретных интервалов P:

S[k]=1P⋅S(kP).{\displaystyle S[k]={\frac {1}{P}}\cdot S\left({\frac {k}{P}}\right).}

∫P(∑m=−∞∞s(t−mP))⋅e−2iπkPtdt=∫−∞∞s(t)⋅e−2iπkPtdt⏟=defS(kP){\displaystyle \int _{P}\left(\sum _{m=-\infty }^{\infty }s(t-mP)\right)\cdot e^{-2i\pi {\frac {k}{P}}t}\,dt=\underbrace {\int _{-\infty }^{\infty }s(t)\cdot e^{-2i\pi {\frac {k}{P}}t}\,dt} _{{\stackrel {\mathrm {def} }{=}}\,S\left({\frac {k}{P}}\right)}}

Достаточным условием для восстановления s(t) (и таким образом S( f )) только из этих элементов (то есть из ряда Фурье) является то, что ненулевой отсчет s(t) будет ограничен известным интервалом длиной P, с удвоением частотной области в соответствии с теоремой отсчетов Найквиста-Шеннона.

• Conte, S. D.; de Boor, Carl. Elementary Numerical Analysis (неопр.). — Third. — New York: McGraw Hill, Inc., 1980. — ISBN 0-07-066228-2.
• Evans, L. Partial Differential Equations (неопр.). — American Mathematical Society, 1998. — ISBN 3-540-76124-1.
• Howell, Kenneth B. Principles of Fourier Analysis (неопр.). — CRC Press, 2001. — ISBN 978-0-8493-8275-8.
• Kamen, E. W.; Heck, B. S. Fundamentals of Signals and Systems Using the Web and Matlab (англ.). — 2. — Prentiss-Hall, 2000. — ISBN 0-13-017293-6.
• Knuth, Donald E. The Art of Computer Programming Volume 2: Seminumerical Algorithms (англ.). — 3rd. — Addison-Wesley Professional, 1997. — P. Section 4.3.3.C: Discrete Fourier transforms, pg.305. — ISBN 0-201-89684-2.
• Müller, Meinard. The Fourier Transform in a Nutshell (неопр.). — Springer, 2015. — С. In Fundamentals of Music Processing, Section 2.1, p. 40—56. — ISBN 978-3-319-21944-8. — doi:10.1007/978-3-319-21945-5.
• Polyanin, A. D.; Manzhirov, A. V. Handbook of Integral Equations (неопр.). — Boca Raton: CRC Press, 1998. — ISBN 0-8493-2876-4.
• Rudin, Walter. Fourier Analysis on Groups (неопр.). — Wiley-Interscience, 1990. — ISBN 0-471-52364-X.
• Smith, Steven W. The Scientist and Engineer's Guide to Digital Signal Processing (англ.). — Second. — San Diego: California Technical Publishing, 1999. — ISBN 0-9660176-3-3.
• Stein, E. M.; Weiss, G. Introduction to Fourier Analysis on Euclidean Spaces (англ.). — Princeton University Press, 1971. — ISBN 0-691-08078-X.

Преобразование Фурье — Национальная библиотека им. Н. Э. Баумана

Материал из Национальной библиотеки им. Н. Э. Баумана
Последнее изменение этой страницы: 22:47, 17 ноября 2016.

Преобразование Фурье — операция взятия интеграла Фурье от функции вещественной переменной, результатом которой является новая функция, описывающая амплитуды при разложении исходной функции на гармонические колебания с разными частотами.

Аналогично ряду Фурье, имеет вещественную и комплексную формы.

Вещественный интеграл Фурье

Как правило, большая часть оптических и электрических сигналов имеет непериодический характер и поэтому представляются непереодическими вещественными функциями. Непериодические функции не могут быть разложены в ряд Фурье, однако любую такую функцию s(x){\displaystyle s(x)\,\!} всегда можно считать периодической с периодом Tx→ ∞{\displaystyle T_{x}\to \ \infty \,\!}.

Пусть полученная периодическая функция удовлетворяет условиям Дирихле (определена на всей числовой оси, имеет конечное число точек разрыва на каждом конечном промежутке и абсолютно интегрируема ∫−∞∞|s(x)|dx< ∞{\displaystyle \int \limits _{-\infty }^{\infty }|s(x)|\,dx<\ \infty \,\!}), что всегда выполняется на практике для рассматриваемых сигналов. Тогда посредством предельного перехода получается разложение s(x){\displaystyle s(x)\,\!} в так называемый вещественный (тригонометрический) интеграл Фурье:

s(x)=∫0∞dνx∫−∞∞s(u)cos⁡[2πνx(x−u)]du=2∫0∞[acos(νx)cos⁡(2πxνx)+bsin(νx)sin⁡(2πxνx)]dνx,(1.1){\displaystyle s(x)=\int \limits _{0}^{\infty }\,d\nu _{x}\int \limits _{-\infty }^{\infty }s(u)\cos {\big [}2\pi \nu _{x}(x-u){\big ]}\,du=2\int \limits _{0}^{\infty }{\big [}a_{\cos }(\nu _{x})\cos(2\pi x\nu _{x})+b_{\sin }(\nu _{x})\sin(2\pi x\nu _{x}){\big ]}\,d\nu _{x},\quad \quad {\color {Maroon}(1.1)}\,\!}

где acos(νx)=∫−∞∞s(u)sin⁡[2πνxu]du(1.2){\displaystyle a_{\cos}(\nu_{x}) = \int\limits_{-\infty}^{\infty} s(u)\sin\big[ 2\pi\nu_{x}u\big] \, du \quad {\color{Maroon}(1.2)} \,\! } — косинус-преобразование Фурье;

bsin(νx)=∫−∞∞s(u)cos⁡[2πνxu]du(1.3){\displaystyle b_{\sin}(\nu_{x}) = \int\limits_{-\infty}^{\infty} s(u)\cos\big[ 2\pi\nu_{x}u\big] \, du \quad {\color{Maroon}(1.3)} \,\! } — синус-преобразование Фурье;

νx{\displaystyle \nu _{x}\,\!} — текущее значение пространственной (временной) частоты.

Интеграл Фурье (1.1){\displaystyle \color {Maroon}(1.1)\,\!} представляет вещественную функцию s(x){\displaystyle s(x)\,\!} в виде суммы бесконечного числа косинусоидальных гармоник с амплитудой dA=acos(νx)dνx{\displaystyle dA=a_{cos}(\nu _{x})d\nu _{x}\,\!} и синусоидальных гармоник с амплитудой dB=bsin(νx)dνx{\displaystyle dB=b_{sin}(\nu _{x})d\nu _{x}\,\!} при непрерывно изменяющейся частоте 0≤νx< ∞{\displaystyle 0\leq \nu _{x}<\ \infty \,\!}.

В зависимости от физического смысла переменной x говорят о непрерывном вещественном спектре амплитуд acos(νx){\displaystyle a_{cos}(\nu _{x})\,\!} и bsin(νx){\displaystyle b_{sin}(\nu _{x})\,\!} несмещенных по фазе косинусоидальных и синусоидальных гармоник или о непрерывном вещественном спектре амплитуд acos(νt),bsin(νt){\displaystyle a_{cos}(\nu _{t}),b_{sin}(\nu _{t})\,\!}которые также называют вещественной спектральной плотностью амплитуд косинусоидальных и синусоидальных гармоник соответственно.

Выражение (1.1){\displaystyle \color {Maroon}(1.1)\,\!} можно преобразовать к виду:

s(x)=∫0∞dcos(nux)cos⁡[2πxνx+ϕ(nux)]dνx(1.4){\displaystyle s(x)=\int \limits _{0}^{\infty }d_{\cos }(nu_{x})\cos {\big [}2\pi x\nu _{x}+\phi (nu_{x}){\big ]}\,d\nu _{x}\quad \quad {\color {Maroon}(1.4)}\,\!}

где dcos(νx)=acos2(νx)+bsin2(νx){\displaystyle d_{\cos }(\nu _{x})={\sqrt {a_{\cos }^{2}(\nu _{x})+b_{\sin }^{2}(\nu _{x})}}\,\!};

ϕ(νx)=arctan⁡−bsin(νx)acos(νx){\displaystyle \phi (\nu _{x})=\arctan {\frac {-b_{\sin }(\nu _{x})}{a_{\cos }(\nu _{x})}}\,\!};

cos⁡ϕ(νx)=acos(νx)d(νt){\displaystyle \cos {\phi }(\nu _{x})={\frac {a_{\cos }(\nu _{x})}{d(\nu _{t})}}\,\!};

sin⁡ϕ(νx)=−bsin(νx)ϕ(νt){\displaystyle \sin {\phi }(\nu _{x})=-{\frac {b_{\sin }(\nu _{x})}{\phi (\nu _{t})}}\,\!}.

В зависимости от представления сигнала говорят о непрерывных вещественных пространственно-частотных спектрах амплитуд dcos(νx){\displaystyle d_{\cos }(\nu _{x})\,\!} и фаз ϕ(νx){\displaystyle \phi (\nu _{x})\,\!} или о непрерывных вещественных частотно-временных спектрах амплитуд dcos(νt){\displaystyle d_{\cos }(\nu _{t})\,\!} и фаз ϕ(νt){\displaystyle \phi (\nu _{t})\,\!} смещенных по фазе косинусоидальных гармоник. Эти спектры часто называют вещественной спектральной плотностью амплитуд и фаз, при этом частоты непрерывно заполняют действительную полуось 0≤νx< ∞,0≤νt< ∞{\displaystyle 0\leq \nu _{x}<\ \infty ,0\leq \nu _{t}<\ \infty \,\!}, а функции dcos{\displaystyle d_{\cos }\,\!} и ϕ{\displaystyle \phi \,\!} задают закон распределения амплитуд и начальных фаз в зависимости от частоты. В результате интеграл Фурье представляет вещественную функцию s(x){\displaystyle s(x)\,\!} в виде суммы бесконечного числа смещенных по фазе косинусоидальных гармоник с амплитудой dD=dcos(νx)dνx{\displaystyle dD=d_{\cos }(\nu _{x})d\nu _{x}\,\!} при непрерывно изменяющейся частоте.

Тригонометрический интеграл Фурье (1.1){\displaystyle \color {Maroon}(1.1)\,\!} обычно применяют для разложения в вещественный спектр непериодических многомерных и электрических сигналов, описываемых четными или нечетными функциями. Для четной функции (1.1){\displaystyle \color {Maroon}(1.1)\,\!} имеет вид косинус-интеграла Фурье из несмещенных по фазе косинусоидальных гармоник:

schet(x)=2∫0∞acoschet(νx)cos⁡(2πxνx)dνx(1.5){\displaystyle s^{chet}(x)=2\int \limits _{0}^{\infty }a_{\cos }^{chet}(\nu _{x})\cos(2\pi x\nu _{x})\,d\nu _{x}\quad \quad {\color {Maroon}(1.5)}\,\!}

где косинус-преобразование Фурье (1.2){\displaystyle \color {Maroon}(1.2)\,\!} имеет вид acoschet(νx)=2∫0∞schet(x)cos⁡(2πxνx)dx(1.6){\displaystyle a_{\cos }^{chet}(\nu _{x})=2\int \limits _{0}^{\infty }s^{chet}(x)\cos(2\pi x\nu _{x})\,dx\quad \quad {\color {Maroon}(1.6)}\,\!}

В случае нечетной функции имеем синус-интеграл Фурье, задающий непрерывное разложение по не смещенным по фазе синусоидальным гармоникам:

snechet(x)=2∫0∞bsinchet(νx)sin⁡(2πxνx)dνx(1.7){\displaystyle s^{nechet}(x)=2\int \limits _{0}^{\infty }b_{\sin }^{chet}(\nu _{x})\sin(2\pi x\nu _{x})\,d\nu _{x}\quad \quad {\color {Maroon}(1.7)}\,\!}

где синус-преобразование Фурье (1.3){\displaystyle {\color {Maroon}(1.3)}\,\!} имеет вид bsinnechet(νx)=2∫0∞snechet(x)sin⁡(2πxνx)dx(1.8){\displaystyle b_{\sin }^{nechet}(\nu _{x})=2\int \limits _{0}^{\infty }s^{nechet}(x)\sin(2\pi x\nu _{x})\,dx\quad {\color {Maroon}(1.8)}\,\!}

Формулы (1.5){\displaystyle \color {Maroon}(1.5)\,\!} – (1.8){\displaystyle \color {Maroon}(1.8)\,\!} обычно используют вместо (1.1){\displaystyle \color {Maroon}(1.1)\,\!} – (1.3){\displaystyle \color {Maroon}(1.3)\,\!} для временных сигналов s(t){\displaystyle s(t)\,\!}, так как последние заданы для t≥0{\displaystyle t\geq 0\,\!} и могут быть продолжены на всю действительную ось четным или нечетным образом.

Комплексный интеграл Фурье

Переход к комплексному виду интеграла Фурье осуществляется в результате предельного перехода Tx→∞{\displaystyle T_{x}\to \infty \,\!} в комплексном ряде Фурье так, что νx1=1Txdνx,νxk=kTxdνx,ckdc=s~(νx)dνx{\displaystyle \nu _{x1}={\frac {1}{T_{x}}}d\nu _{x},\quad \nu _{xk}={\frac {k}{T_{x}}}d\nu _{x},\quad c_{k}dc={\tilde {s}}(\nu _{x})d\nu _{x}\,\!}. В результате комплексный интеграл Фурье принимает вид:

s(x)=∫−∞∞[∫−∞∞s(u)e−i2πνxudu]ei2πνxxdνx,(2.1){\displaystyle s(x) = \int\limits_{-\infty}^{\infty} \bigg[ \int\limits_{-\infty}^{\infty} s(u)e^{-i2\pi\nu_xu}\, du \bigg] e^{i2\pi\nu_xx}\, d\nu_x, \quad \quad {\color{Maroon}(2.1)} \,\! }

где s~(νx)=F{s(x)}=∫−∞∞s(x)e−i2πνxxdx=acos(νx)−ibsin(νx)(2.2){\displaystyle {\tilde {s}}(\nu _{x})=F{\big \{}s(x){\big \}}=\int \limits _{-\infty }^{\infty }s(x)e^{-i2\pi \nu _{x}x}\,dx=a_{\cos }(\nu _{x})-ib_{\sin }(\nu _{x})\quad \color {Maroon}(2.2)\,\!} называют прямым преобразованием Фурье или Фурье-образом функции s(x){\displaystyle s(x)\,\!}.

При этом из сравнения (2.1){\displaystyle \color {Maroon}(2.1)\,\!} с (1.6){\displaystyle \color {Maroon}(1.6)\,\!} и (1.8){\displaystyle \color {Maroon}(1.8)\,\!} следует, что для четной и нечетной функции имеют место равенства:

s~chet(νx)=acoschet(νx),s~nechet(νx)=−ibsinnechet(νx){\displaystyle {\tilde {s}}^{chet}(\nu _{x})=a_{\cos }^{chet}(\nu _{x}),\quad {\tilde {s}}^{nechet}(\nu _{x})=-ib_{\sin }^{nechet}(\nu _{x})\,\!}

Обычно s~(νx)=|s~(νx)|eiϕsin(νx){\displaystyle {\tilde {s}}(\nu _{x})=|{\tilde {s}}(\nu _{x})|e^{i\phi _{\sin }(\nu _{x})}\,\!} называют непрерывным комплексным спектром или комплексной спектральной плотностью, которую графически изображают в виде спектральной плотности амплитуд as(nux)=|s~(νx)|{\displaystyle a_{s}(nu_{x})=|{\tilde {s}}(\nu _{x})|\,\!} и спектральной плотности фаз ϕs(νx)=arg[s~(νx)]{\displaystyle \phi _{s}(\nu _{x})=arg[{\tilde {s}}(\nu _{x})]\,\!} для −∞< νx< ∞{\displaystyle -\infty <\ \nu _{x}<\ \infty \,\!}. При x=t{\displaystyle x=t\,\!} говорят о непрерывном комплексном частотно-временном спектре s~(νt)=|s~(νt)|eiϕsin(νx){\displaystyle {\tilde {s}}(\nu _{t})=|{\tilde {s}}(\nu _{t})|e^{i\phi _{sin}(\nu _{x})}\,\!} , который удобно вычислять для всех частот. Очевидно, отрицательные временные частоты по-прежнему не имеют физического смысла. Выражение, восстанавливающее исходный сигнал (прообраз) по комплексной спектральной плотности, имеет вид:

s(x)=F−1{s~(x)}=∫−∞∞s~(νx)ei2πxνxdνx(2.3){\displaystyle s(x)=F^{-1}{\big \{}{\tilde {s}}(x){\big \}}=\int \limits _{-\infty }^{\infty }{\tilde {s}}(\nu _{x})e^{i2\pi x\nu _{x}}\,d\nu _{x}\quad \quad \color {Maroon}(2.3)\,\!}

Это выражение называют обратным преобразованием Фурье. Оно показывает, что функцию s(x){\displaystyle s(x)\,\!} можно представить в виде суммы бесконечного числа комплексных экспоненциальных гармоник с амплитудой dc=s~(νx)dνx{\displaystyle dc={\tilde {s}}(\nu _{x})d\nu _{x}\,\!} и непрерывно изменяющейся частотой−∞< νx< ∞{\displaystyle -\infty <\ \nu _{x}<\ \infty \,\!}. По аналогии с комплексным рядом Фурье говорят о разложении сигнала на выходе транспаранта (1.5){\displaystyle \color {Maroon}(1.5)\,\!} в виде непрерывной суммы дифрагировавших вверх и вниз плоских волн. При этом переход к комплексному интегралу Фурье является также естественным физическим обобщением разложения по плоским волнам комплексного непериодического сигнала, учитывающего как амплитудную, так и фазовую модуляцию объекта.

В случае вещественной функции s(x){\displaystyle s(x)\,\!} интеграл Фурье (2.1){\displaystyle \color {Maroon}(2.1)\,\!} служит комплексным обобщением тригонометрического интеграла Фурье (1.1){\displaystyle \color {Maroon}(1.1)\,\!}. Действительно, из (2.1){\displaystyle \color {Maroon}(2.1)\,\!} имеем

s(x)=∫−∞∞dνx∫−∞∞s(u)e−i2πνx(x−u)du==∫−∞∞dνx∫−∞∞s(u)cos⁡[2πνx(x−u)]du+∫−∞∞dνx∫−∞∞s(u)sin⁡[2πνx(x−u)]du(2.4){\displaystyle {\begin{aligned}s(x)&=\int \limits _{-\infty }^{\infty }\,d\nu _{x}\int \limits _{-\infty }^{\infty }s(u)e^{-i2\pi \nu _{x}(x-u)}\,du=\\&=\int \limits _{-\infty }^{\infty }\,d\nu _{x}\int \limits _{-\infty }^{\infty }s(u)\cos {\big [}2\pi \nu _{x}(x-u){\big ]}\,du+\int \limits _{-\infty }^{\infty }\,d\nu _{x}\int \limits _{-\infty }^{\infty }s(u)\sin {\big [}2\pi \nu _{x}(x-u){\big ]}\,du\end{aligned}}\quad \quad {\color {Maroon}(2.4)}\,\!}

Так как для вещественной функции первый внутренний интеграл является четной, а второй внутренний интеграл – нечетной функцией от νx{\displaystyle \nu _{x}\,\!}, то первое слагаемое в (2.4){\displaystyle \color {Maroon}(2.4)\,\!} удваивается, а второе равно нулю. Тогда с необходимостью (2.4){\displaystyle \color {Maroon}(2.4)\,\!} переходит в (1.1){\displaystyle \color {Maroon}(1.1)\,\!}.

С помощью прямого преобразование Фурье (2.2){\displaystyle \color {Maroon}(2.2)\,\!} удобно вычислять коэффициенты ck{\displaystyle c_{k}\,\!} комплексного ряда Фурье, если известен Фурье-образ финитного импульса simp(x)=speriod(x)rect(xTx){\displaystyle s_{imp}(x)=s_{period}(x)rect({\frac {x}{T_{x}}})\,\!} , порождающего периодическую функцию speriod{\displaystyle s_{period}\,\!} . Рассматривая его для определенности на промежутке −Tx2≤x≤Tx2{\displaystyle -{\frac {T_{x}}{2}}\leq x\leq {\frac {T_{x}}{2}}\,\!} и доопределяя нулем в оставшихся точках действительной оси, с учетом (2.2){\displaystyle \color {Maroon}(2.2)\,\!} получим:

ck(νxk)=1Tx∫−∞∞simp(x)e−i2πνxkxdx=1Txs~imp(νxk){\displaystyle c_{k}(\nu _{xk})={\frac {1}{T_{x}}}\int \limits _{-\infty }^{\infty }s_{imp}(x)e^{-i2\pi \nu _{xk}x}\,dx={\frac {1}{T_{x}}}{\tilde {s}}_{imp}(\nu _{xk})\,\!}

Таким образом, коэффициенты ck{\displaystyle c_{k}\,\!} с точностью до множителя 1Tx{\displaystyle {\frac {1}{T_{x}}}\,\!} совпадают с ординатами комплексной спектральной плотности s~imp(νxk){\displaystyle {\tilde {s}}_{imp}(\nu _{xk})\,\!} в точках νxk{\displaystyle \nu _{xk}\,\!}. При этом если Tx→∞{\displaystyle T_{x}\to \infty \,\!}, то s~imp(νxk)→s~(νx){\displaystyle {\tilde {s}}_{imp}(\nu _{xk})\to {\tilde {s}}(\nu _{x})\,\!}.

Многомерные интегралы и преобразования Фурье

По аналогии с многомерными рядами Фурье, для упрощения математических выкладок многомерные интегралы Фурье также удобнее рассматривать в комплексной форме. Непериодическая функция двух переменных может быть представлена двумерным комплексным интегралом Фурье:

s(x,y)=∫−∞∞∫−∞∞[∫−∞∞∫−∞∞s(u,v)e−i2π(νxu+νyv)dudv]ei2π(xνx+yνy)dνxdνy{\displaystyle s(x,y)=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }{\bigg [}\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }s(u,v)e^{-i2\pi (\nu _{x}u+\nu _{y}v)}dudv{\bigg ]}e^{i2\pi (x\nu _{x}+y\nu _{y})}d\nu _{x}d\nu _{y}\,\!}

Прямое двумерное преобразование Фурье имеет вид:

s~(νx,νy)=F{s(x,y)}=∫−∞∞∫−∞∞s(x,y)e−i2π(νxx+νyy)dxdy(3.1){\displaystyle {\tilde {s}}(\nu _{x},\nu _{y})=F{\big \{}s(x,y){\big \}}=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }s(x,y)e^{-i2\pi (\nu _{x}x+\nu _{y}y)}dxdy\quad \quad {\color {Maroon}(3.1)}\,\!}

или

s~(ν→)=∫−∞∞∫−∞∞s(r→)e−i2πν→r→)dr→{\displaystyle {\tilde {s}}({\vec {\nu }})=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }s({\vec {r}})e^{-i2\pi {\vec {\nu }}{\vec {r}})}d{\vec {r}}\,\!},

где ν→=(νx,νy),r=(x,y){\displaystyle {\vec {\nu }}=(\nu _{x},\nu _{y}),\quad r=(x,y)\,\!}

На практике двумерный Фурье-образ s~(νx,νy)=|s~(νx,νy)|eiϕs(νx,νy){\displaystyle {\tilde {s}}(\nu _{x},\nu _{y})=|{\tilde {s}}(\nu _{x},\nu _{y})|e^{i\phi _{s}(\nu _{x},\nu _{y})}\,\!} называют двумерным непрерывным комплексным ПЧС или двумерной комплексной спектральной плотностью, которую графически изображают в виде двумерной спектральной плотности амплитуд as(νx,νy)=|s~(νx,νy)|{\displaystyle a_{s}(\nu _{x},\nu _{y})=|{\tilde {s}}(\nu _{x},\nu _{y})|\,\!} и двумерной спектральной плотности фаз ϕs(νx,νy)=arg[s~(νx,νy)]{\displaystyle \phi _{s}(\nu _{x},\nu _{y})=arg[{\tilde {s}}(\nu _{x},\nu _{y})]\,\!} , рассматриваемых в двумерном частотном пространстве R2(nux,νy){\displaystyle R^{2}(nu_{x},\nu _{y})\,\!}.

Для двумерного обратного преобразования Фурье получим:

s(x,y)=F−1{s~(νx,νy)}∫−∞∞s~(νx,νy)ei2π(xνx+yνy)dνxdνy(3.2){\displaystyle s(x,y)=F^{-1}{\big \{}{\tilde {s}}(\nu _{x},\nu _{y}){\big \}}\int \limits _{-\infty }^{\infty }{\tilde {s}}(\nu _{x},\nu _{y})e^{i2\pi (x\nu _{x}+y\nu _{y})}\,d\nu _{x}d\nu _{y}\quad \quad {\color {Maroon}(3.2)}\,\!}

или s(r→)=∫−∞∞∫−∞∞s~(ν→)ei2πν→r→dν→{\displaystyle s({\vec {r}})=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }{\tilde {s}}({\vec {\nu }})e^{i2\pi {\vec {\nu }}{\vec {r}}}\,d{\vec {\nu }}\,\!}

Прямое и обратное преобразование Фурье для функции трех переменных в общем виде можно записать аналогичным образом:

s~(νx,νy,νt)=∫−∞∞∫−∞∞∫−∞∞s(x,y,t)e−i2π(νxx+νyy+

Преобразование Фурье

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Страница проекта на GitHub.

Содержание

Предельный переход от ряда Фурье к преобразованию Фурье Пояснения понятия спектральной плотности сигнала Связь спектральной плотности непериодического сигнала и огибающей коэффициентов ряда Фурье Условия существования преобразования Фурье Список литературы

Предельный переход от ряда Фурье к преобразованию Фурье

Использование периодических функций для представления периодических сигналов выглядит вполне логичным и позволяет перевести анализ в частотную область. Таким образом, мы можем заменить сигнал набором спектральных гармоник , путем разложения в ряд Фурье:

(1)

где  — период повторения сигнала. Спектр состоит из дискретных гармоник, равноотстоящих по частоте с шагом рад/с.

Однако, периодические функции могут быть использованы и для частотного представления непериодических сигналов. В данном разделе мы произведем переход от ряда Фурье (1) к интегральному преобразованию Фурье для непериодических сигналов .

Для начала рассмотрим, что будет происходить, если мы будем увеличивать период повторения периодического сигнала. На рисунке 1 показаны временные осциллограммы периодической последовательности прямоугольных импульсов , а также амплитудный спектр , при различном периоде повторения с, с и с, при амплитуде сигнала равной 2 В.

Рисунок 1. Амплитудный спектр периодической последовательности прямоугольных импульсов
при увеличении периода повторения

Из рисунка 1 видно, что при увеличении периода , гармоники спектра приближаются друг к другу, потому что расстояние между гармониками  обратно пропорционально периоду . Амплитуды гармоник при этом уменьшаются из-за уменьшения средней мощности сигнала на одном периоде повторения.

При увеличении периода повторения до бесконечности, периодический сигнал становится непериодическим, расстояние между гармониками  уменьшатся до нуля (дискретные гармоники сольются в одну сплошную линию), а амплитуды гармоник уменьшатся до бесконечно-малых значений.

Подставим в уравнение (1) для сигнала выражение для коэффициентов ряда Фурье :

(2)

Непериодический сигнал можно получить как предельный переход периодического сигнала (2) при стремящимся к бесконечности:

(3)

Учитывая, что , множитель переходит в бесконечно-малое приращение частоты:

(4)

Значения частот дискретных гармоник:

(5)

и (3) с учетом (4) и (5):

(6)

Сумма бесконечно-малых площадей, где  — основание прямоугольника переходит в интеграл, а переходит в непрерывную переменную :

(7)

Окончательно, из выражения (7) можно выделить пару интегральных преобразований Фурье для непериодического сигнала:

(8)

(9)

Уравнение (8) определяет прямое преобразование Фурье непериодического сигнала. Прямое преобразование Фурье обозначается оператором , ставит в соответствие сигналу непрерывную функцию частоты , которая носит название спектральной плотности сигнала .

Выражение (9) представляет собой обратное преобразование Фурье, которое обозначается оператором и позволяет восстановить сигнал  по его спектральной плотности .

В терминах частоты , выраженной в Гц, с учетом , уравнения (8) и (9) принимают вид:

(10)

(11)

Пояснения понятия спектральной плотности сигнала

Часто спектральную плотность непериодического сигала называют спектром, что не совсем корректно, потому что не определяет конечные амплитуды гармоник сигнала, как это было при разложении периодического сигнала в ряд Фурье, а задает распределение энергии сигнала по оси частот. Для пояснения отличия понятия спектра периодического сигнала от спектральной плотности непериодического сигнала рассмотрим следующую аналогию.

Пусть имеется стержень длины м, единичной площади , который состоит из сегментов сплава меди и алюминия в различных пропорциях, как это показано на рисунке 2.

Рисунок 2. Стрежень состоящий из сегментов
сплава меди и алюминия в различных пропорциях

Каждый сегмент имеет постоянную плотность , где , но различные сегменты имеют различную плотность. Масса стержня может быть представлена как сумма масс всех сегментов:

(12)

где  — конечные массы отдельных сегментов.

Также как стержень в приведенном примере состоит из отдельных сегментов конечных масс, так и периодический сигнал состоит из суммы дискретных гармоник конечной амплитуды, в соответствии с рядом Фурье.

Предположим теперь, что такой же стержень представляет собой непрерывно-меняющийся по длине сплав меди и алюминия, как это показано на рисунке 3.

Рисунок 3. Стрежень состоящий из непрерывного по длине
сплава меди и алюминия

Плотность такого стержня непрерывно уменьшается по длине. Тогда массу мы не можем представить как сумму конечных дискретных масс, а только как интеграл плотности по длине стержня:

(13)

Другими словами, конечная масса состоит из бесконечного числа бесконечно-малых масс . Размерность плотности при постоянной площади стержня можно выразить в единицах кг/м.

Аналогично, спектральная плотность непериодического сигнала есть непрерывная функция частоты . При этом каждой бесконечно-малой полосе соответствует амплитуда , по аналогии бесконечно-малых масс из которых состоит полная масса стержня.

Единица измерения плотности в приведенном примере кг/м, тогда единица измерения равна сигнал/(единицу полосы), или Вс, если характеризует изменение напряжения. Таким образом, размерность спектральной плотности непериодического сигнала отличается от размерности спектра периодического сигнала и эти два термина отождествлять не следует.

Связь спектральной плотности непериодического сигнала и огибающей коэффициентов ряда Фурье

В предыдущем параграфе мы привели пояснения понятия спектральной плотности непериодического сигнала физической аналогией с плотностью непрерывного сплава двух металлов. Мы говорили, что спектральная плотность непериодического сигнала представляет собой непрерывную функцию частоты . При этом каждой частоте соответствует бесконечно-малая амплитуда , спектра сигнала.

И хотя физический смысл спектральной плотности отличается от физического смысла спектра периодического сигнала, равно как масса стержня отличается от плотности, но оба этих представления находятся в тесной связи друг с другом. Эту взаимосвязь спектра периодического сигнала и спектральной плотности мы проследим на примере одиночного импульса длительности и его периодических копий.

Пример одиночного импульса показан на рисунке 4 сплошной линией. Обратим внимание, что исходный импульс ограничен по длительности, т.е. при .

Рисунок 4. Периодическое повторение одиночного импульса

Периодический сигнал , показанный на рисунке 4 пунктиром, представляет собой бесконечную сумму копий сигнала , сдвинутых друг относительно друга по времени на величину (чтобы импульсы не перекрывались во времени).

Преобразование Фурье одиночного импульса равно:

(14)

Периодический сигнал имеет дискретный спектр , где , , который равен:

(15)

Сравнивая (14) и (15) на фиксированной секте частот , можно заключить, что:

(16)

Таким образом, если периодический сигнал представляет собой повторенный импульс длительности , то его спектр на сетке частот равен значению спектральной плотности одиночного импульса , деленного на период повторения . При этом приводит размерность спектральной плотности к размерности спектра (равно как объем тела приводит размерность плотности к размерности массы тела).

Непрерывная по частоте спектральная плотность, деленная на период повторения задает непрерывную огибающую дискретного спектра , как это показано на рисунке 5 пунктирной линией.

Рисунок 5. Cпектральная плотность как непрерывная огибающая дискретного спектра

Забегая немного вперед, можем заметить, что периодическое повторение одиночного импульса привело к дискретизации непрерывной по частоте огибающей и переходу к дискретному спектру . Мы еще будем подробно рассматривать этот вопрос в следующих главах.

Условия существования преобразования Фурье

Мы осуществили передельный переход от периодического сигнала к непериодическому при устремлении периода повторения к бесконечности. При увеличении периода длительность сигнала не увеличивалась. Это можно видеть на рисунке 1, длительность импульса остается постоянной при увеличении периода повторения .

Таким образом мы можем утверждать, что преобразование Фурье (8) и (9) существует для всех ограниченных во времени сигналов , для которых выполняется условие Дирихле [1, стр. 165].

Представим теперь, что сигнал не является ограниченным во времени, но затухает настолько быстро, что выполняется условие:

(17)

Говорят, что  — абсолютно интегрируемая функция времени [2, стр. 510], если выполняется (17).

Рисунок 6. График функции

В качестве примера абсолютно интегрируемой функции можно привести , график которой показан на рисунке 6. Поскольку затухает достаточно быстро, то всегда найдется такое конечное , при котором ошибка представления в виде ряда Фурье функции на интервале (при отбрасывании «затухающих хвостов») будет меньше любой конечной величины. Другими словами, «затухающие хвосты» с ростом периода будут оказывать исчезающе слабое влияние.

Таким образом, функция может быть бесконечной, но носить затухающий характер, и при условии абсолютной интегрируемости функции , мы можем использовать преобразование Фурье для расчета ее спектральной плотности.

Можно заметить, что всякий ограниченный во времени сигнал, удовлетворяющий условиям Дирихле также является абсолютно интегрируемым.

Приведенные рассуждения не являются строгим математическим доказательством условий существования преобразования Фурье, а скорее дают интуитивно-понятное разъяснение (17). Строгое доказательство условий существования преобразования Фурье можно найти [1, стр. 199] или в [2, стр. 511].

Выводы

В данном разделе мы рассмотрели предельных переход от периодического сигнала к непериодическому и получили выражения для прямого и обратного интегрального преобразования Фурье.

Мы отметили, что в отличии от спектра периодических сигналов, преобразование Фурье непериодического сигнала возвращает спектральную плотность сигнала, выраженную в единицах измерения сигнала, деленного на частоту. Были даны необходимые пояснения к понятию спектральной плотности.

Также были рассмотрены условия существования преобразования Фурье.

В следующих разделе мы рассмотрим свойства преобразования Фурье, a также спектральные плотности некоторых сигналов.

Смотри также

Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов
Информация была полезна? Поделитесь с друзьями!

Список литературы

[1] Воробьев Н.Н. Теория рядов. Москва, Наука, Главная редакция физико-математической литературы, 1979, 408 с.

[2] Будак, Б.М., Фомин, С.В. Кратные интегралы и ряды. Москва, Наука, 1965, 608 c.

[3] Баскаков, С.И. Радиотехнические цепи и сигналы Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[4] Гоноровский И.С. Радиотехнические цепи и сигналы Москва, Советское радио, 1977, 608 c.

[5] Дёч, Г. Руководство по практическому применению преобразования Лапласа. Москва, Наука, 1965, 288 c.

[6] Bracewell, R. The Fourier Transform and Its Applications McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

© Бахурин Сергей 2015 - 2020. Все права защищены. Любое копирование материалов сайта без разрешения автора запрещено.

---

Смотрите также

• 
  Белые точки на гландах что это такое
• 
  Пиломатериал что это такое
• 
  Букинг что это такое
• 
  Перманентный макияж что это такое фото
• 
  Лазерная кавитация что это такое
• 
  Металлолом 5а что это такое
• 
  Это что же такое будет если все умными стянуть харатьян
• 
  Факоэмульсификация катаракты что это такое
• 
  Иммобилайзер что это такое в машине фото
• 
  Терморегулятор что это такое
• 
  Перкуссия в медицине что это такое