Самый сложный математический пример в мире
Математики решили самую сложную задачу в мире
Одна из самых сложных математических загадок в мире поддалась математикам Эндрю Сазерленду из США и Эндрю Букеру из Бристольского университета в Британии. Они вычислили три числа, сумма кубов которых будет равна 42. На расчеты понадобился миллион часов машинного времени.
Задача, поставленная еще в 1954 году, выражена следующим уравнением: x³ + y³ + z³ = k. K — каждое из чисел от 1 до 100. Требовалось найти x, y и z.
Греф признался в ненависти к школе и экзаменам
ПодробнееВ течение десятков лет математики искали решения для целых чисел от единицы до 100. Ученым удалось найти значения для всех чисел, кроме 33 и 42. Задачу 33 в итоге решили — это сделал британец Эндрю Букер, который написал новый алгоритм вычислений и прогнал решение через мощный компьютер. Решение было найдено за три недели. Оставалось число 42.
Букер решил заручиться поддержкой своего заокеанского коллеги Эндрю Сазерленда, уточнил сайт Science Alert. Для решения задачи ученые решили использовать сеть Charity Engine, которая объединяет более полумиллиона персональных компьютеров по всему миру в глобальную вычислительную сеть.
На решение задачи потребовалось более миллиона часов машинного времени. В итоге планетарный разум выдал три числа. Целиком уравнение выглядит так: (-80538738812075974)³ + 80435758145817515³ + 12602123297335631³ = 42.
70человек поделились статьей
Задачи современной математики, которые до сих пор не решены
Как и всегда в математике, если проблема не решается «в лоб», к ней подходят с другого конца. Например, в 2013 году было доказано, что количество простых чисел, отличающихся на 70 миллионов, бесконечно. Тогда же, с разницей менее чем в месяц, значение разницы было улучшено до 59 470 640, а затем и вовсе на порядок — до 4 982 086. На данный момент существуют теоретические обоснования бесконечности пар простых чисел с разницей в 12 и 6, однако доказанной является лишь разность в 246. Как и прочие проблемы такого рода, гипотеза о числах-близнецах особенно важна для криптографии.
Гипотеза Римана
Если кратко, то Бернхард Риман предположил, что распределение простых чисел по множеству всех натуральных чисел не подчиняется каким-либо законам. Но их количество на заданном участке числового ряда коррелирует с распределением определенных значений на графике дзета-функции. Она расположена выше и для каждого s дает бесконечное количество слагаемых. Например, когда в качестве s подставляется 2, то в результате получается уже решенная “базельская задача” — ряд обратных квадратов (1 + 1/4 + 1/9 + 1/16 + …).
Одна из “проблем тысячелетия”, за решение которой назначен приз в миллион долларов, а также вхождение в пантеон “богов” современной математики. На деле, доказательство этой гипотезы настолько сильно толкнет вперед теорию чисел, что это событие по праву будет называться историческим. Многие вычисления и утверждения в математике строятся на предположении о том, что “гипотеза Римана” верна, и до сих пор никого не подводили. Немецкий математик сформулировал знаменитую задачу 160 лет назад, и с тех пор к ее решению подступались неисчислимое количество раз, однако прогресс очень скромен.
Реально сложные задачи
В отличие от предыдущей задачи, здесь решение намного сложнее, потому что в голове нужно держать одновременно 2-3 условия, которыми надо проверять числа. Но мы справимся.
Для решения нам понадобится вспомнить, что такое простые числа и в чём их особенность. Простое число — то, которое может делиться нацело только на себя и на единицу. Например, число 5 — простое, потому что делится только на 5 и на 1. А число 6 — не простое, потому что кроме 6 и 1 оно ещё делится на 2 и 3 без остатка. Семь тоже будет простым числом, а восемь — нет, потому что кроме 8 и 1 оно делится также на 2 и 4.
Если перемножить два простых числа, то полученное произведение больше никак нельзя получить другим способом (кроме умножения этого же числа на единицу). Поясним на примере.
Возьмём два простых числа 5 и 7 и перемножим их — получится 35. Больше число 35 получить никак не получится, кроме как умножить 35 на 1. Это значит, что если произведение можно разложить на два простых множителя, то других вариантов разложения (кроме числа и единицы) у него не будет. Это нам пригодится при решении задач — и если число можно разложить на 2 простых, то и их сумму тоже легко сразу посчитать.
Ещё пример:
54 = 2 × 27
54 = 3 × 18
54 = 6 × 9, а это значит, что число 54 нельзя получить перемножением двух простых чисел и нельзя сразу сказать, чему однозначно равна сумма множителей.
И ещё:
21 = 3 × 7
Оба числа простые, поэтому произведение 21 можно получить только из них, а значит, легко посчитать сумму — она будет равна 3 + 7 = 10.
Теперь переведём их диалог на язык математики и логики и обозначим числа как n и m:
Первый: Я понял, что одно из чисел точно не простое, потому что иначе я сразу бы разложил число на произведение двух простых и легко получил сумму. А раз так, то это одно из чисел m или n можно получить перемножением двух других чисел. Поэтому общее произведение состоит не менее чем из трёх множителей, причём как минимум один из них отличается от остальных — поэтому получается несколько вариантов возможных сумм, и я не знаю, какая из них правильная (пометим это как Правило 1).
Второй: Сумму, которая у меня есть, нельзя получить из двух простых чисел, поэтому и твоё произведение тоже нельзя разложить на два простых множителя. Это значит, что у меня нечётная сумма, потому что, по гипотезе Гольдбаха, в нашем случае можно получить любое чётное число, сложив два простых. А раз это не два простых числа, значит, и сумма будет нечётная. А ещё эта сумма точно не равна сумме двух и простого числа, потому что два — тоже простое, ха! Поэтому есть несколько вариантов суммы m и n, которые подходят под твои условия, но я не могу пока определить, какие именно (пометим это как Правило 2).
Первый: Из всех множителей моего произведения я могу составить только один вариант пары, сумма которой подойдёт под твоё ограничение — не будет разбиваться на сумму двух простых или сумму чисел одного множителя (Правило 3).
Второй: Ах вот как! Из всех вариантов пар, на которые можно разбить сумму и подходящих под твои условия, есть только одна, которая позволила бы тебе определить это (Правило 4). Теперь и мне понятно, что это за числа!
Теперь подберём варианты суммы, которая была у второго. Ограничения такие:
- нечётная;
- не равна сумме двойки и простого числа.
1 — не подходит, потому что оба числа больше единицы.
2, 4, 6, 8… — нет, потому что чётные.
3 — нет, потому что это сумма двойки и простого числа.
5 — нет, по той же причине (2 + 3).
7 — тоже нет (2 + 5).
9 — тоже нет (2 + 7, а 7 — простое число).
11 — подходит.
13 — нет, потому что 13 = 2 + 11 (11 — простое число).
15 — нет, потому что 15 = 2 + 13 (13 — тоже простое число).
17 — подходит.
19 — нет, потому что 19 = 2 + 17 (17 — простое число).
…
Способ подбора суммы понятен, дальше можно продолжать по тому же алгоритму. Мы же выберем те, которые нам уже подошли, и на их примере покажем, что нужно делать дальше, чтобы получить правильный ответ. Наши числа, которые нам подходят уже сейчас: 11 и 17. Начнём с 11.
Сумма = 11.
Найдём все слагаемые, которые могут давать эту сумму:
2 + 9
3 + 8
4 + 7
5 + 6
Для каждого из них запишем произведение и проверим, выполняется ли Правило 3, которое сказал первый программист.
Смотрим на произведение 2 × 9 = 18 и как ещё его можно получить.
18 = 2 × 9 → Да (Правило 3 выполняется).
18 = 3 × 6 → Нет (Правило 3 не работает, потому что 3 + 6 = 9, а 9 можно получить из простых чисел 2 и 7).
Смотрим на произведение 3 × 8 = 24.
24 = 2 × 12 → Нет (чётная сумма, Правило 2 не работает).
24 = 3 × 8 → Да (выполняется Правило 3).
24 = 6 × 4 → Нет (чётная сумма).
Смотрим на произведение 4 × 7 = 28.
28 = 2 × 14 → Нет (чётная сумма).
28 = 4 × 7 → Да (выполняется Правило 3).
Смотрим на произведение 5 × 6 = 30.
30 = 2 × 15 → Да.
30 = 3 × 10 → Нет (Правило 3 не работает, потому что 3 + 10 = 13, а 13 можно получить суммой простых чисел 2 и 11).
30 = 5 × 6 → Да.
Тут мы вообще не можем выбрать одну пару, потому что Правило 3 выполняется 2 раза, а значит, этот вариант отбрасываем.
Получается, что для суммы 11 могут быть три варианта произведений, для которых выполняется Правило 3: 2 и 9, 3 и 8, 4 и 7. Но тогда Правило 4 не выполняется, потому что нужно, чтобы для одной суммы была только одна пара, которая подходит под правило 3. Продолжаем искать.
Сумма = 17.
Найдём все слагаемые, которые могут давать эту сумму:
2 + 15
3 + 14
4 + 13
5 + 12
6 + 11
7 + 10
8 + 9
Для каждого из них запишем произведение и проверим, выполняется ли Правило 3, которое сказал первый программист.
Смотрим на произведение 2 × 15 = 30 и как ещё его можно получить.
30 = 2 × 15 → Да.
30 = 3 × 10 → Нет (Правило 3 не работает, потому что 3 + 10 = 13, а 13 можно получить суммой простых чисел 2 и 11).
30 = 5 × 6 → Да.
Тут мы вообще не можем выбрать одну пару, потому что Правило 3 выполняется 2 раза, а значит, этот вариант отбрасываем.
Смотрим на произведение 3 × 14 = 42 и как ещё его можно получить:
42 = 2 × 21 → Да.
42 = 3 × 14 → Да.
42 = 6 × 7 → Нет.
Два раза выполняется Правило 3 — отбрасываем пару.
Смотрим на произведение 4 × 13 = 52 и как ещё его можно получить.
52 = 2 × 26 → Нет.
52 = 4 × 13 → Да.
Смотрим на произведение 5 × 12 = 60 и как ещё его можно получить.
60 = 2 × 30 → Нет.
60 = 3 × 20 → Да.
60 = 5 × 12 → Да.
60 = 6 × 10 → Нет.
Два раза выполняется Правило 3 — отбрасываем пару.
Смотрим на произведение 6 × 11 = 66 и как ещё его можно получить.
66 = 2 × 33 → Да.
66 = 3 × 22 → Нет.
66 = 6 × 11 → Да.
Два раза выполняется Правило 3 — отбрасываем пару.
Смотрим на произведение 7 × 10 = 70 и как ещё его можно получить.
70 = 2 × 35 → Да.
70 = 5 × 14 → Нет.
70 = 7 × 10 → Да.
Два раза выполняется Правило 3 — отбрасываем пару.
Смотрим на произведение 8 × 9 = 72 и как ещё его можно получить.
72 = 2 × 36 → Нет.
72 = 3 × 24 → Да.
72 = 4 × 18 → Нет.
72 = 6 × 12 → Нет.
72 = 8 × 9 → Да.
Два раза выполняется Правило 3 — отбрасываем пару.
Получается, что для суммы 17 может быть только один вариант произведения, для которого выполняется Правило 3: это 4 и 13. А значит, что Правило 4 тоже выполняется и мы нашли нужные числа!
Если вы дочитали досюда и всё поняли — снимаем шляпу. Вы не из тех, кого могут испугать вычисления и логический подход!
7 самых сложных логических задач, которые решит только один человек из десяти
7 самых сложных логических задач, которые решит только один человек из десяти
В связи с началом учебного года мы решили проверить, насколько наши подписчики умны и изобретательны. А ты сможешь решить все, представленные нами, задачи?
«ПОСЧИТАЙ-КА»
Давай проверим, умеешь ли ты считать?
Реши без помощи калькулятора вот этот пример: К 1000 нужно прибавить 40, потом еще 1000. Затем приплюсуйте 30. Есть? Теперь снова 1000. Добавьте 20. Еще раз 1000. И напоследок 10.
Сколько получилось?
А теперь проверь все еще раз с помощью своего телефона. Совпало?
«ЧТО БОДРИТ УТРОМ?»
А теперь задачка на логику.
Женщина уронила в стакан, полный кофе, свой перстень. Как он мог остаться сухим?
Как ты думаешь, в чем тут секрет?
«СПИЧКИ ДЕТЯМ НЕ ИГРУШКА»
Сколько спичек на картинке?
«ЗЕЛЕНЫЙ ЧЕЛОВЕЧЕК»
Это та загадка, которую ты решишь с помощью детской наивностью. Мы уверены, её можно отгадать с первого раза! Ответь на вопрос: что нужно сделать, когда видишь зеленого человечка?
Учитель рисует на листке бумаги несколько кружков и спрашивает одного ученика: «Сколько здесь кружков?». «Семь» — отвечает ученик. «Правильно. Так сколько здесь кружков?» — опять спрашивает учитель другого ученика. «Пять» — отвечает тот. «Правильно» — снова говорит учитель. Так сколько же кружков он нарисовал на листке?
Думаешь все так легко? А теперь попробуй решить задачи, которые считаются самыми сложными в мире!
«СУПЕР СУДОКУ»
Первое, над чем мы предлагаем тебе поломать голову – это самая сложная судоку в мире.
Судоку – это японская головоломка с числами. Принцип ее совсем не замысловат. Но ту, которую предложили тебе мы, сможет решить точно не каждый!
«БОГИ ЛОГИЧЕСКИХ ЗАДАЧ»
Есть три бога, A, B, и C, один из которых бог истины, другой бог лжи и третий бог случая, причём неясно, кто из них кто. Бог истины всегда говорит правду, бог лжи обманывает, а бог случая может сказать и то, и другое в произвольном порядке. Необходимо определить, кем является каждый из богов, задав три вопроса, на которые можно ответить «да» или «нет», при этом каждый вопрос задаётся только одному богу. Боги понимают вопросы, но отвечают на своём языке, в котором есть слова «da» и «ja», но неизвестно, какое слово обозначает «да», а какое «нет».
Эта логическая задача за авторством американского философа и логика Джорджа Булоса была впервые опубликована в итальянской газете «la Repubblica» в 1992-м году. Так же в загадке есть комментарии создателей:
– Можно задавать одному богу более чем один вопрос (поэтому другим богам может быть не задано ни одного вопроса вообще).
– Каков будет следующий вопрос и кому он будет задан, может зависеть от ответа на предыдущий вопрос.
– Бог случая отвечает случайным образом, зависящим от подбрасываний монетки, спрятанной в его голове: если выпадет аверс, то отвечает правдиво, если реверс — то врёт.
– Бог случая отвечает «da» или «ja» на любой вопрос, на который можно ответить «да» либо «нет».
Ответы на все задачи можно посмотреть по ссылке.
Found a typo in the text? Select it and press ctrl + enter
Когда математика становится слишком сложной / Хабр
Математики давно пытаются привыкнуть к тому, что некоторые задачи в принципе невозможно решить

Мы любим повторять, что всё возможно. В книге Джастера Нортона «Мило и волшебная будка» король отказывается сообщить Мило, что его цель недостижима, поскольку «многое становится возможным, если не знаешь, что оно невозможно» [правда, это слова других персонажей книги / прим. перев.]. Но в реальном мире некоторые вещи и вправду невозможны, и мы можем доказать это при помощи математики.
Люди используют термин «невозможно» разными способами. Он может описывать просто маловероятные вещи – такие, как найти две одинаковых колоды перемешанных карт. Он может описывать задачи, практически невозможные по причине отсутствия времени, места или ресурсов – такие, как переписать всю Библиотеку Конгресса от руки. Устройства типа вечного двигателя невозможны физически, поскольку их существование противоречило бы нашему пониманию физики.
Математическая невозможность – это другое. Мы начинаем с недвусмысленных предположений, и, используя математические рассуждения и логику, заключаем, что некоторые исходы событий невозможны. Никакая удача, настойчивость, время или навыки не сделают задачу выполнимой. История математики полнится доказательствами невозможности. Многие из них считаются наиболее примечательными результатами математики. Но так было не всегда.
Кара за, возможно, самое первое доказательство невозможности, была строгой. Историки считают, что в пятом веке до н.э. Гиппас из Метапонта, последователь Пифагора, обнаружил, что невозможно найти отрезок, которым можно было бы измерить как длину стороны, так и длину диагонали правильного пятиугольника. Сегодня мы говорим, что длина диагонали правильного пятиугольника со стороной длины 1 – золотое сечение, ϕ = 1/2 (1 + √5) – является иррациональным числом. Открытие Гиппаса стало вызовом кредо Пифагора, «всё есть число», поэтому легенды говорят, что Гиппаса либо утопили в море, либо просто изгнали из рядов пифагорейцев.
Более века спустя Евклид возвысил прямую и круг, сочтя их фундаментальными кривыми геометрии. Впоследствии многие поколения геометров чертили всякое – делили углы, проводили перпендикуляры, и так далее – только при помощи циркуля и линейки. Однако определённые конструкции, казавшиеся простыми, поставили греческих геометров в тупик, приобрели в итоге мифический статус, и раздражали математиков более 2000 лет. Это задачи деления произвольного угла на три части, построение стороны куба, объём которого в два раза превышает объём заданного, построение всех правильных многоугольников, а также построение квадрата с площадью, равной площади заданного круга.
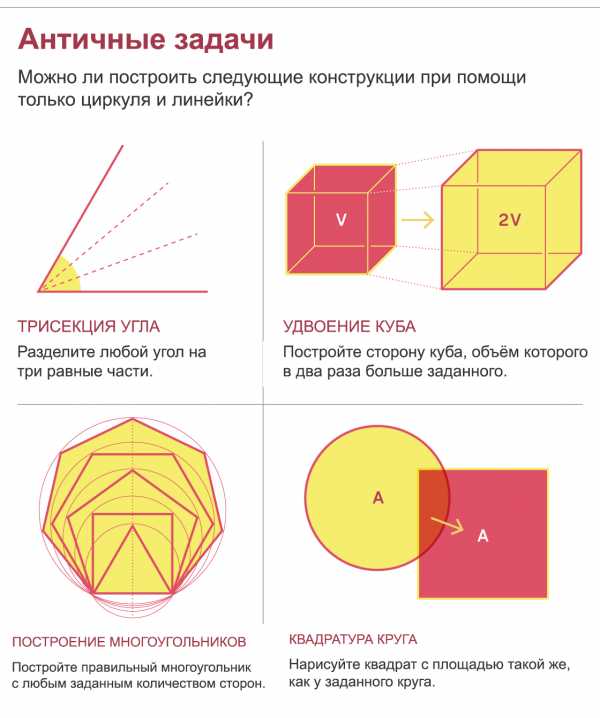
Хотя задачи эти по своей природе геометрические, доказательство невозможности их решения таковым не является. Чтобы продемонстрировать невозможность их решения, потребовалась новая математика.
В XVII века Рене Декарт сделал фундаментальное открытие: если мы ограничим себя только циркулем и линейкой, мы не сможем строить отрезки любой длины. Если мы начнём с отрезка длиной 1, мы сможем строить только такие отрезки, длину которых можно выразить при помощи целых чисел, сложения, вычитания, умножения, деления и извлечения квадратного корня (как золотое сечение).
Поэтому одной из стратегий поиска доказательства невозможности решения геометрической задачи – то есть, что некий объект нельзя построить – будет показать, что длину некоего отрезка итоговой фигуры нельзя выразить указанным способом. Но для того, чтобы это строго показать, потребовалась зарождавшаяся тогда алгебра.
Два столетия спустя соотечественник Декарта, Пьер Лоран Ванцель, использовал многочлены (суммы коэффициентов и переменных, возведённых в степень) и их корни (переменные, при подстановке которых многочлен становится равным нулю) для атаки на эти классические задачи. К примеру, в задаче удвоения куба сторона куба с объёмом, удвоенным по сравнению с объёмом единичного куба, должна быть равной . Это корень многочлена x3-2, поскольку .
В 1837 Ванцель доказал, что для того, чтобы отрезок можно было построить при помощи циркуля и линейки, его длина должна быть корнем многочлена, который нельзя разложить на множители, и чья степень (наивысшая степень переменной) является степенью двойки. Например, золотое сечение является корнем многочлена второй степени x2 − x − 1. Но x3-2 – это многочлен третьей степени, поэтому построить нельзя. Поэтому Ванцель заключил, что удвоить куб невозможно.
Сходным образом он доказал, что невозможно использовать классические инструменты для трисекции любого угла или построения определённых правильных многоугольников – к примеру, семистороннего. Интересно, что все три доказательства невозможностей были размещены на одной странице. Как у Исаака Ньютона и Альберта Эйнштейна были свои annus mirabilis (годы чудес), так и эту ситуацию можно назвать pagina mirabilis – страницей чудес.
Доказательство невозможности оставшейся задачи, квадратуры круга, потребовала чего-то нового. В 1882 году Фердинанд фон Линдеман доказал ключевой момент – что число π нельзя построить – доказав его трансцендентность, то есть, что оно не является корнем никакого многочлена.
Этим классическим задачам можно приписать дурную репутацию и считать их сиренами, заманивавшими математиков, чтобы те разбивались об острые скалы невозможности. Но я считаю их музами, вдохновлявшими многие поколения творческих мыслителей.
То же касается и более новой невозможной задачи, возникающей из такого простого действия, как переход через мост. Представьте, что вы живёте в Питтсбурге, «городе мостов», как многие из моих учеников. Какой-нибудь велосипедист, любящий приключения, может задуматься – можно ли, начав поездку из дома, проехать ровно один раз по каждому из 22 мостов, пересекающих основные реки Питтсбурга, и вернуться домой.
В 1735 году прусский мэр поставил аналогичную задачу перед Леонардом Эйлером, только для Кёнигсберга (ныне Калининград). Семь мостов этого города объединяют три берега реки и остров. Сначала Эйлер отмёл эту задачу, как не математическую: «Решения такого рода мало связаны с математикой, и я не понимаю, почему вы ожидаете, что его выдаст вам математик, а не кто-либо ещё».
Однако вскоре Эйлер доказал невозможность решения этой задачи, и в процессе создал новую область математики, названную им геометрией расположений – то, что мы сегодня называем топологией. Он понял, что конкретные детали – точные расположения мостов, форма участков земли, и т.п. – были не важны. Важны были только их связи. Позднее математики уточнили формулировки Эйлера с использованием того, что мы сегодня называем графами. Идея связности лежит в основе изучения социальных сетей, интернета, эпидемиологии, лингвистики, планирования оптимальных маршрутов, и т.д.
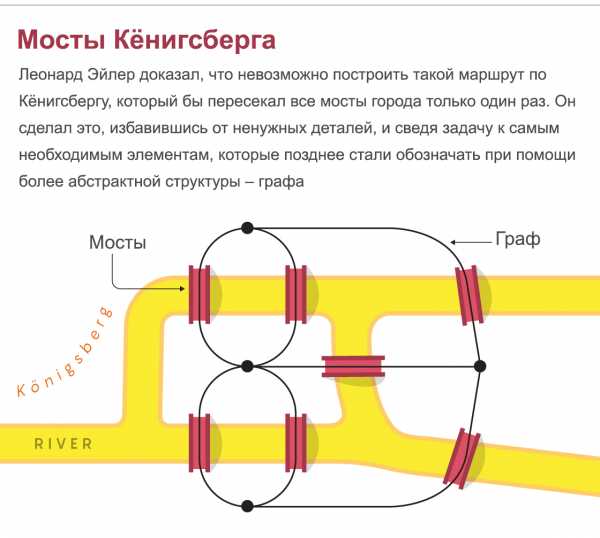
Мосты Кёнигсберга: Леонард Эйлер доказал, что невозможно построить такой маршрут по Кёнигсбергу, который бы пересекал все мосты города только один раз. Он сделал это, избавившись от ненужных деталей, и сведя задачу к самым необходимым элементам, которые позднее стали обозначать при помощи более абстрактной структуры – графа.
Доказательство Эйлера было удивительно простым. Он рассудил, что каждый раз, когда мы приходим, а потом уходим с конкретного участка земли, мы должны исключить два моста. Поэтому на каждый участок земли должно вести чётное количество мостов. Но поскольку на каждый участок Кёнигсберга вело нечётное количество мостов, построить такой маршрут было невозможно. Сходным образом три моста, ведущие на остров Герз на реке Аллегейни в Питтсбурге, делают невозможным построение искомого велосипедного маршрута.
Как показывает эта задача, невозможности не ограничиваются абстрактной математикой. У них могут быть последствия и в реальном мире – иногда даже политические.
Недавно математики обратились к такому понятию, как джерримендеринг. В США после каждой переписи штаты должны переделывать избирательные округа. Но иногда правящая партия переписывает их границы смехотворным образом для максимизации своих политических сил.
Во многих штатах есть требование «компактности» округов, не имеющего строгого математического определения. В 1991 году Дэниел Полсби и Роберт Поппер предложили 4πA/P2 в качестве способа измерения компактности округа площади A и периметра P. Эти значения варьируются от 1 для круглого округа до почти нуля у деформированных округов с длинным периметром.
Тем временем Николас Стефанопулос и Эрик Макги ввели в 2014 году понятие «разрыва эффективности» в качестве меры политической честности плана изменения округов. Две разных стратегии джерримендеринга заключаются либо в том, чтобы у оппозиции в округе оказалось менее 50% голосов, или около 100%. Каждая из этих тактик заставляет оппозицию терять голоса, теряя нужных кандидатов, или тратя голоса на тех, кому это не нужно. Разрыв эффективности описывает относительное количество утерянных голосов.
Обе эти меры полезны для распознавания джерримендеринга. Но в 2018 году Борис Алексеев и Дастин Миксон доказали, что «иногда небольшого разрыва эффективности можно достичь при помощи округов странной формы». То есть, математически невозможно всегда рисовать округа так, чтобы они удовлетворяли и требованиям Полсби-Поппера, и честности в плане разрыва эффективности.
Однако обнаружение и предотвращение тайных методов джерримендеринга – это активно развивающаяся область, привлекающая многих талантливых исследований. Как и с проблемами античности или с задачей о мостах Кёнигсберга, я уверен, проблема джерримендеринга вдохновит творческий подход и поспособствует развитию математики.
Более сложные примеры уравнений | Математика
52. Более сложные примеры уравнений.
Пример 1.
5/(x – 1) – 3/(x + 1) = 15/(x2 – 1)
Общий знаменатель есть x2 – 1, так как x2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x2 – 1. Получим:
или, после сокращения,
5(x + 1) – 3(x – 1) = 15
или
5x + 5 – 3x + 3 = 15
или
2x = 7 и x = 3½
Рассмотрим еще уравнение:
5/(x-1) – 3/(x+1) = 4(x2 – 1)
Решая, как выше, получим:
5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.
Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.
Для первого примера получим:
Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.
Для второго примера получим:
5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0
Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.
Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.
Пример 2.
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:
(x + 3) (2x – 2) = (2x + 3) (x – 1)
или
2x2 + 6x – 2x – 6 = 2x2 + 3x – 2x – 3.
Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x2. Однако, мы можем от обеих частей уравнения вычесть по 2x2 — от этого уравнение не нарушится; тогда члены с x2 уничтожатся, и мы получим:
6x – 2x – 6 = 3x – 2x – 3
Перенесем неизвестные члены влево, известные вправо — получим:
3x = 3 или x = 1
Вспоминая данное уравнение
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.
Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:
2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,
что невозможно.
Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:
(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)
Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:
6x + 10 = 2x + 18
или
4x = 8 и x = 2
Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:
или 11 = 11
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:
(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x2 + 4x – 10 = 2x2 + 16x – 18.
Здесь уже члены с x2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы
4x2 – 12x = –8
или
x2 – 3x = –2
Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:
1) 22 – 3 · 2 = –2 и 2) 12 – 3 · 1 = –2
Если мы вспомним начальное уравнение
(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),
то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.
Пример 3.
Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:
1) x2 – 5x + 6 = x2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),
2) x2 – x – 2 = x2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),
3) x2 – 2x – 3 = x2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).
Общий знаменатель равен (x – 3)(x – 2)(x + 1).
Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:
на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:
3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.
Отсюда получим:
–x = –13 и x = 13.
Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.
Если бы мы взяли уравнение:
то, поступая совершенно так же, как выше, получили бы
3(x + 1) – 2(x – 3) = x – 2
или
3x + 3 – 2x + 6 = x – 2
или
3x – 2x – x = –3 – 6 – 2,
откуда получили бы
0 = –11,
что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.
15 самых сложных вопросов по SAT математике

Хотите проверить себя, отвечая на самые сложные вопросы по математике SAT? Хотите знать, что делает эти вопросы такими сложными и как их лучше всего решать? Если вы готовы по-настоящему погрузиться в математический раздел SAT и нацелиться на этот высший балл, то это руководство для вас.
Мы собрали то, что мы считаем , из 15 самых сложных вопросов для текущего SAT , со стратегиями и ответами на каждый из них.Все это сложные вопросы SAT Math из практических тестов SAT College Board, а это значит, что их понимание - один из лучших способов учиться для тех из вас, кто стремится к совершенству.
Изображение: Соня Севилья / Викимедиа
Краткий обзор SAT Math
Третий и четвертый разделы теста SAT всегда будут математическими разделами . Первый математический подраздел
.21 самый сложный вопрос по математике для ACT
Вы учились и теперь готовы к математическому разделу ACT (ууу!). Но готовы ли вы ответить на самые сложные математические вопросы, которые предлагает ACT? Вы хотите точно знать, почему эти вопросы так сложны и как их лучше всего решать? Если вы настроены на этот высший балл (или вам просто очень любопытно посмотреть, какие будут самые сложные вопросы), то это руководство для вас.
Мы собрали, по нашему мнению, 21 самый сложный вопрос, который ACT задавал студентам за последние 10 лет, со стратегиями и ответами на каждый из вопросов.Все это настоящие вопросы по математике ACT, поэтому их понимание и изучение - один из лучших способов улучшить свой текущий результат ACT и выбить его из общего ряда в день экзамена.
Краткий обзор раздела ACT Math
Как и все тематические разделы ACT, математический раздел ACT представляет собой один законченный раздел, который вы будете изучать сразу. Это всегда будет второй раздел теста, и у вас будет 60 минут, чтобы ответить на 60 вопросов .
ACT размещает свои вопросы
. Самая сложная математическая задача в мире. |
17 безумных фактов о самом сложном классе математики в Гарварде "Math 55"
«Математика 55» приобрела репутацию самого сложного курса математики для студентов Гарварда - и, судя по этой оценке, возможно, в мире. Многие студенты боятся этого курса, а некоторые записываются из чистого любопытства, чтобы понять, о чем идет речь. (Сообщается, что в первый день каждого семестра класс проводится только стоя.) Но немногие избранные считают это обрядом посвящения, который свойственен их математическим способностям.
Двухсеместровый курс, состоящий из «Абстрактной алгебры с отличием» (Math 55a) осенью и «Honors Real and Complex Analysis» (Math 55b) весной, - намного сложнее чем вы могли бы поверить в его скромное название. Но, по общему мнению, это стоит того, чтобы пройти через испытания. Поскольку очень немногие из нас когда-либо получат шанс начать курс, не говоря уже о его завершении, вот 17 безумных вещей, которые вы, вероятно, не знаете, о самом сумасшедшем академическом опыте, который большинство из нас когда-либо могло себе представить.И если вы хотите проверить свои собственные алгебраические навыки (или их отсутствие), не пропустите эти 20 вопросов по математике для начальной школы, которые так усложняют, что вы удивитесь, как вы закончили обучение.

 Shutterstock
Shutterstock Чтобы понять, какой мозг требуется для прохождения Math 55, примите во внимание, что Сам Билл Гейтс был студентом этого курса. (Он прошел.) И если вы хотите отточить свой мозг, как соучредитель Microsoft, вот 5 книг, которые, по словам Билла Гейтса, вам следует прочитать.

 Shutterstock
Shutterstock Один бывший студент Гарварда, называющий себя «поклонницей математики 55», сказал The Harvard Crimson : «Эти ребята - мои образцы для подражания.«И ученик 55-летнего возраста (так себя называют студенты математики 55) мог подтвердить: когда люди узнают, они« просто спонтанно воспламеняются, падают в обморок, теряют сознание, становятся ярко-красными, начинают хихикать ».
Или просто просят помочь с домашним заданием.


Согласно справочнику для первокурсников факультета математики Гарварда, есть два курса математики для первого года обучения, самый сложный из которых - Math 55. Вы можете пройти Math 21, который преподают аспиранты и где домашнее задание обычно занимает от трех до шести часов. в неделю.Или вы можете выбрать математику 55, что даст вам в 10 раз больше объема домашнего задания.
«На выполнение наборов задач может уйти от 24 до 60 часов в неделю». Да, в неделю . Так что, по сути, это работа на полную ставку плюс работа на неполную ставку - и это в дополнение к остальной части вашей учебной нагрузки, стажировок, любых реальных концертов с неполной занятостью и необходимых вечеринок в Гарварде.

 Shutterstock
Shutterstock Как автор Сэм Уильямс описывает в Free as in Freedom свою биографию пионера свободного программного обеспечения (и выпускника математики 55) Ричарда Столлмана , курс рассчитан на «четыре года математики за два семестра. .«
Профессор Пенсильванского университета Дэвид Харбатер , бывший коллега в возрасте 55 лет, добавляет: «Можно с уверенностью сказать, что никогда не было такого интенсивного и продвинутого класса для начинающих студентов». Другими словами: это похоже на обучение «с большой скоростью». И, говоря о безумной учебной программе, ознакомьтесь с 20 самыми нелепыми университетскими курсами, в которые вы не поверите, что они реальны.

 Shutterstock
Shutterstock Вы можете ожидать, что студенты будут регулярно отказываться от программы Math 55.К окончанию семестра размер класса сокращается до половины или меньше от первоначального. По словам одного студента, который изучал математику 55 в 2005 году и вел постоянный подсчет посещаемости: «У нас был 51 студент в первый день, 31 студент во второй день, 24 в течение следующих четырех дней, 23 в течение еще двух недель, а затем 21. на оставшуюся часть первого семестра после пятого понедельника.


По общему мнению, те, кто выживает в первые пять недель - конец гарвардского периода, когда они перестают работать, - становятся толстыми как воры.Они должны; этого требует курсовая работа. Итак, они проводят время вместе, вместе веселятся, вместе делают домашнее задание.
Домашнее задание выполняется в освещенной флуоресцентными лампами общей комнате Тайер Холла, общежития на северной стороне Гарвардского двора. (Кстати, Стив Баллмер , Э. Каммингс и Энди Боровиц - все они, кстати, пожили там в годы учебы в Гарварде.) 55 Военная комната.«Мы команда, пытающаяся выжить в этом классе, - говорит один из 55. - Нет никаких претензий. Никакого отношения «Мы лучше всех» ».

 Shutterstock
Shutterstock «Это определенно культ», - сказал The Harvard Crimson Раймонд Т. Пьерумберт, профессор Оксфордского университета, в прошлом 55-летний (он проходил курс в 70-х). "Я рассматриваю это как больше испытание, чем курс. Люди, которые прошли через это, на самом деле не забывают об этом ... Это как смена кольца братства.Он вас идентифицирует ».

 Shutterstock / Smolaw
Shutterstock / Smolaw Большинство студентов, изучающих математику 55, каждую неделю создают наборы задач объемом от 15 до 20 страниц. Им приходится производить так много, что ученикам иногда не рекомендуется показывать слишком много своих работ.
Как объясняет один из бывших сотрудников 55 лет: «Многие студенты выписывают решения в форме леммы-теоремы, доказывая все с самого начала. Я тоже это делал. Это делает вашу задачу огромной … Вы должны узнать, в чем основная идея Доказательства есть, и то, что можно принять как должное.Это не так просто сделать на студенческом курсе доказательства, где почти все доказательства основаны на очевидных фактах ».
 Shutterstock
Shutterstock В книге Уильямса он описывает книгу Ричарда Столлмана «Математика 55», завершающую семестр с 20 студентами, восемь из которых впоследствии станут профессорами математики. В конце концов один стал преподавать физику.

 Shutterstock
Shutterstock Те, кто записывается на Math 55, могут задаться вопросом, действительно ли они в состоянии справиться с этим.Что ж, это выясняется довольно быстро, благодаря диагностическому обследованию абитуриентов. Студентам, набравшим более 50 процентов, рекомендуется записаться на курс «Математика 55», а тем, кто набрал менее 10 процентов, рекомендуется пройти курс «Математика 21. Если вы окажетесь посередине, выбор за вами».

 Shutterstock
Shutterstock Согласно справочнику для первокурсников, Math 55 «часто содержит бывших членов команд Международной математической олимпиады». Это всемирный чемпионат, в котором учащиеся старших классов математики из более чем 100 стран соревнуются друг с другом, решая до смешного сложные математические задачи.
Например, вот задача из прошлогоднего боя:
Выпуклый четырехугольник ABCD удовлетворяет условию AB · CD = BC · DA. Точка X находится внутри
ABCD, так что
∠XAB = ∠XCD и ∠XBC = ∠XDA.
Докажите, что ∠BXA + ∠DXC = 180◦
Удачи.

 Shutterstock
Shutterstock На курсы Math 55 записывается намного больше мужчин, чем женщин. Согласно отчету Harvard Crimson , с 1990 по 2006 год курс прошли всего 17 женщин.В 2015 году ни одна женщина не завершила математику 55a.

 Shutterstock
Shutterstock Профессор Юм-Тонг Сиу, чей класс начался с 50 студентов в 2003 году, сказал, что он активно пытался сократить размер класса. Как сообщает The Harvard Independent , в классе осталось 25 студентов, но Сиу добавила: «Я хочу еще немного сократить». Цель: 20. «Нам нужна группа студентов с аналогичным опытом, чтобы мы могли двигаться в темпе, который подходит им одновременно, чтобы они не скучали и не скучали», - сказал Сиу.


Сосед из двух человек 55 объяснил Harvard Independent , что «в одну особенно напряженную ночь решения проблем он спал больше, чем они двое вместе взятых, а всего у него было всего шесть часов!»


«Если проблема занимает полтора часа, чтобы решить и описать ее, я бы назвал ее простой», - сказал The Harvard Independent один студент. Для сравнения, это примерно столько же, сколько средний анимационный фильм Диснея.


Тех, кто планирует поступить в Math 55, предупреждают, что математика должна быть их делом . Это не класс для дилетантов, которые хотят изучать философию или заниматься политикой на стороне. Как предупреждает руководство для первокурсников, Math 55 предназначена только для тех, кто «достаточно уверен, что вы хотите быть концентратором математики» и кто «хочет, чтобы математика была вашим самым важным предметом».

 Shutterstock
Shutterstock Согласно The Harvard Independent , одно празднование «Дня Пи» в Math 55, которое приходится на 14 марта, потому что число Пи равно 3.14 - оставил треть класса 2002 пьяным. Так что не говорите, что математики тоже не умеют развлекаться! А чтобы после всего этого почувствовать себя немного умнее, ознакомьтесь с этими 40 фактами о числах, которые заставят вас почувствовать себя математическим гением.
Чтобы узнать больше удивительных секретов о том, как прожить свою лучшую жизнь, нажмите здесь , чтобы подписаться на нас в Instagram!
.