Трехмерное измерение что это такое

Трёхмерное пространство — Википедия

Материал из Википедии — свободной энциклопедии

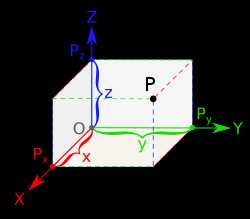Трёхмерная метрика пространства Трёхмерная система координат с осью Х, направленной к читателю У этого термина существуют и другие значения, см. 3D.

Трёхме́рное простра́нство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так как оно имеет три однородных измерения — длину, ширину и высоту, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.

Понимание трёхмерного пространства людьми, как считается, развивается ещё в младенчестве, и тесно связано с координацией движений человека. Визуальная способность воспринимать окружающий мир органами чувств в трёх измерениях называется восприятием глубины.

В аналитической геометрии каждая точка трёхмерного пространства описывается как набор из трёх величин — координат. Задаются три взаимно перпендикулярных координатных оси, пересекающихся в начале координат. Положение точки задаётся относительно этих трёх осей заданием упорядоченной тройки чисел. Каждое из этих чисел задаёт расстояние от начала отсчёта до точки, измеренное вдоль соответствующей оси, что равно расстоянию от точки до плоскости, образованной другими двумя осями.

Также существуют другие системы координат, наиболее часто используются цилиндрическая и сферическая системы.

Другой взгляд даёт линейная алгебра, где важную роль играет понятие линейной независимости. Пространство трёхмерно по той причине, что высота коробки не зависит от её длины и ширины. На языке линейной алгебры пространство трёхмерно, потому что каждая точка может быть задана комбинацией из трёх линейно независимых векторов. В этих терминах пространство-время четырёхмерно, потому что положение точки во времени не зависит от её положения в пространстве.

Трёхмерное пространство имеет несколько свойств, которые отличают его от пространств другой размерности. Например, это пространство наименьшей размерности, в котором можно завязать узел на куске верёвки^[1]. Многие законы физики, например многие законы обратных квадратов связаны с тем что размерность нашего пространства три ^[2].

Нульмерное, одномерное и двухмерное пространства могут рассматриваться как располагающиеся в трёхмерном пространстве; само оно может считаться частью модели четырёхмерного пространства (четвёртым измерением иногда называют время)^[3].

1. ↑ Dale Rolfsen, Knots and Links, Publish or Perish, Berkeley, 1976, ISBN 0-914098-16-0
2. ↑ Brian Greene, The Fabric of the Cosmos, Random House, New York, 2003, ISBN 0-375-72720-5
3. ↑ Четырёхмерное пространство — время (неопр.). Дата обращения 26 февраля 2009.

Трёхмерное пространство - это... Что такое Трёхмерное пространство?

Трёхмерная метрика пространства 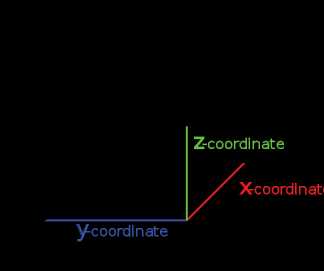Трёхмерная система координат с осью Х направленной к читателю. У этого термина существуют и другие значения, см. 3D.

Трёхме́рное простра́нство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так как оно имеет три однородных измерения — высоту, ширину и длину, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.

Понимание трёхмерного пространства людьми, как считается, развивается ещё в младенчестве, и тесно связано с координацией движений человека. Визуальная способность воспринимать окружающий мир органами чувств в трёх измерениях называется глубиной восприятия.

В аналитической геометрии каждая точка трёхмерного пространства описывается как набор из трёх величин — координат. Задаются три взаимно перпендикулярных координатных оси, пересекающихся в начале координат. Положение точки задаётся относительно этих трёх осей заданием упорядоченной тройки чисел. Каждое из этих чисел задаёт расстояние от начала отсчёта до точки, измеренное вдоль соответствующей оси, что равно расстоянию от точки до плоскости, образованной другими двумя осями.

Также существуют другие системы координат, наиболее часто используются цилиндрическая и сферическая системы.

Другой взгляд даёт линейная алгебра, где важную роль играет понятие линейной независимости. Пространство трёхмерно по той причине, что высота коробки не зависит от её длины и ширины. На языке линейной алгебры пространство трёхмерно, потому что каждая точка может быть задана комбинацией из трёх линейно независимых векторов. В этих терминах пространство-время четырёхмерно, потому что положение точки во времени не зависит от её положения в пространстве.

Трёхмерное пространство имеет несколько свойств, которые отличают его от пространств другой размерности. Например, это пространство наименьшей размерности, в котором можно завязать узел на куске верёвки^[1]. Многие законы физики, например многие законы обратных квадратов связаны с тем что размерность нашего пространства три^[2].

Нульмерное, одномерное и двухмерное пространства могут рассматриваться как располагающиеся в трёхмерном пространстве; само оно может считаться частью модели четырёхмерного пространства (четвёртым измерением континуума, как правило, называют время — неоднородное качество по отношению к пространственной мерности).^[3]

Примечания

1. ↑ Dale Rolfsen, Knots and Links, Publish or Perish, Berkeley, 1976, ISBN 0-914098-16-0
2. ↑ Brian Greene, The Fabric of the Cosmos, Random House, New York, 2003, ISBN 0-375-72720-5
3. ↑ Четырёхмерное пространство — время. Архивировано из первоисточника 18 февраля 2011. Проверено 26 февраля 2009.

См. также

Трехмерное пространство. Почему оно трехмерное?

.

Почему наше пространство трехмерное?

Содержание статьи:

Что такое трехмерное пространство?

Трехмерное пространство – имеет три однородных измерения: высоту, ширину и длину. Это геометрическая модель нашего материального мира.

Чтобы понять природу физического пространства, вначале надо ответить на вопрос о происхождении его размерности. Поэтому значение размерности, как видно, самая значительная характеристика физического пространства.

Размерность пространства

Размерность – наиболее общее количественно выражаемое свойство пространства-времени. В настоящее время физическая теория, претендующая на пространственно-временное описание реальности, берет значение размерности в качестве исходного постулата. Понятие числа измерений, или размерности пространства, относится к наиболее фундаментальным понятиям математики и физики.

Современная физика вплотную подошла к ответу на метафизический вопрос, который был поставлен еще в работах австрийского физика и философа Эрнста Маха: «Почему пространство трехмерное?». Считается, что факт трехмерности пространства связан с фундаментальными свойствами материального мира.

Развитие процесса из точки порождает пространство, т.е. место, где должна происходить реализация программы развития. «Порождаемое пространство «есть для нас форма Вселенной, или форма материи во Вселенной».

Так считали в древности…

Еще Птолемеем было написано на тему о размерности пространства, где он утверждал, что в природе не может существовать более трех пространственных измерений. В своей книге «О небе» еще один греческий мыслитель Аристотель писал, что лишь наличие трех измерений обеспечивает совершенство и полноту мира. Одно измерение, рассуждал Аристотель, образует линию. Если добавить к линии другое измерение, получим поверхность. Дополнение поверхности еще одним измерением образует объемное тело.

Выходит, что «выйти за пределы объемного тела к чему-то другому уже нельзя, так как всякое изменение происходит в силу какого-либо недостатка, а таковой здесь отсутствует. Приведенный ход мысли Аристотеля страдает одной существенной слабостью: остается неясным, по какой причине именно трехмерное объемное тело обладает полнотой и совершенством. В свое время Галилей справедливо высмеял мнение о том, что «число «3» есть число совершенное и что оно наделено способностью сообщать совершенство всему, что обладает троичностью».

Чем определяется мерность пространства

Пространство обладает бесконечной протяженностью по всем направлениям. Однако при этом оно может быть измеряемо лишь в трех независимых друг от друга направлениях: в длину, ширину и высоту; эти направления мы называем измерениями пространства и говорим, что наше пространство имеет три измерения, что оно трехмерное. При этом «независимым направлением мы в этом случае называем линию, лежащую под прямым углом к другой. Таких линий, т.е. лежащих одновременно под прямым углом одна к другой и не параллельных между собою, наша геометрия знает лишь три. То есть мерность нашего пространства определяется количеством возможных в нем линий, лежащих под прямым углом одна к другой. На линии другой линии не может быть – это одномерное пространство. На поверхности возможны 2 перпендикуляра – это двумерное пространство. В «пространстве» три перпендикуляра – это трехмерное пространство».

Почему пространство трехмерное?

Редкий в земных условиях опыт материализации людей часто оказывают на очевидцев физическое воздействие…

Но, в представлениях о пространстве и времени есть еще много неясного, порождающего непрекращающиеся дискуссии ученых. Почему наше пространство имеет три измерения? Могут ли существовать многомерные миры? Возможно ли существование материальных объектов вне пространства и времени?

Утверждение, что физическое пространство обладает тремя измерениями, имеет столь же объективный характер, как и утверждение, к примеру, что существует три физических состояния вещества: твердое, жидкое и газообразное; оно описывает фундаментальный факт объективного мира. И. Кант подчеркнул, что причина трехмерности нашего пространства еще неизвестна. П. Эренфест и Дж. Уитроу показали, что если бы число измерений пространства было больше трех, то существование планетарных систем было бы невозможным – лишь в трехмерном мире могут существовать устойчивые орбиты планет в планетных системах. То есть трехмерный порядок материи является единственно стабильным порядком.

Но трехмерность пространства не может утверждаться как некая абсолютная необходимость. Это физический факт, подобный любому другому, и, как следствие, он подлежит тому же самому виду объяснения.

Вопрос о том, почему наше пространство трехмерное, может решаться или с позиции телеологии, исходящей из ненаучного утверждения, что «трехмерный мир самый совершенный из возможных миров», или с научноматериалистических позиций, основываясь на фундаментальных физических закономерностях.

Мнение современников

Современная физика говорит о том, что характеристика трехмерности состоит в том, что она, и только она, дает возможность формулировать для физической реальности непрерывные причинные законы. Но, «современные концепции не отражают истинного состояния физической картины мира. В наше время ученые рассматривают пространство как некую структуру, состоящую из множества уровней, которые также неопределенны. И потому не случайно современная наука не может дать ответ на вопрос, почему наше пространство, в котором мы живем и которое обозреваем – трехмерное».

Теория связанных пространств

В параллельных мирах события происходят по-своему, они могут…

«Попытки искать ответ на этот вопрос, оставаясь только в пределах математики, обречена на неудачу. Ответ может содержаться в новой малоразработанной области физики». Попробуем найти ответ на этот вопрос исходя из положений рассматриваемой физики связанных пространств.

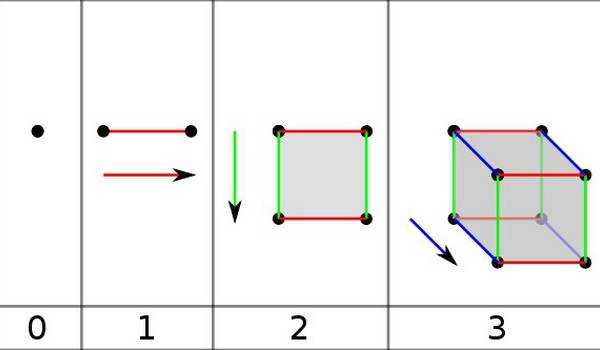
Согласно теории связанных пространств, развитие объекта идет в три этапа, при этом каждый этап развивается вдоль своего выделенного направления, т.е. вдоль своей оси развития.

На первом этапе развитие объекта идет вдоль первоначального выделенного направления, т.е. имеет одну ось развития. На втором этапе происходит поворот системы, образованной на первом этапе, на 90°, т.е. происходит изменение направления пространственной оси, и развитие системы начинает идти вдоль второго выделенного направления, перпендикулярного первоначальному. На третьем этапе снова происходит поворот развития системы на 90°, и она начинает развиваться вдоль третьего выделенного направления, перпендикулярного первым двум. В результате образуются три вложенные друг в друга сферы пространства, каждое из которых соответствует одной из осей развития. Причем все три указанные пространства связаны в единое устойчивое образование физическим процессом.

А потому как данный процесс реализуется на всех масштабных уровнях нашего мира, то все системы, в том числе и сами координаты, построены по триадному (трехкоординатному) принципу. Отсюда следует, что в результате прохождения трех этапов развития процесса естественным образом формируется трехмерное пространство, образованное как следствие физического процесса развития тремя координатными осями трех взаимно перпендикулярных направлений развития!

Эти разумные сущности возникли на самой заре существования Вселенной…

Не зря Пифагору, который, как видно, мог обладать этим знанием, принадлежит выражение: «Все вещи состоят из трех». Об этом же говорится и у Н.К. Рериха: «Символ Триединости имеет огромную древность и встречается во всем Мире, потому он не может быть ограничен какой-либо сектой, организацией, религией или традицией, а также личными или групповыми интересами, потому как представляет эволюцию сознания во всех ее фазах… Знак триединости оказался раскинутым по всему миру… Если собрать вместе все отпечатки того же самого знака, то, возможно, он окажется самым распространенным и древнейшим среди символов человеческих. Никто не может утверждать, что этот знак принадлежит только одному верованию или основан на одном фольклоре».

• Не зря еще в древние времена наш мир представлялся как триединое божество (три слитое в один): нечто одно, целое и неделимое, по своей сакральной значимости намного превосходящее исходные величины.

Мы проследили пространственную специализацию (распределение по координатным направлениям пространства) внутри отдельно взятой системы, но точно такое же распределение мы можем видеть и в любом социуме от атома до галактик. Данные три разновидности пространства являются не чем иным, как тремя координатными состояниями геометрического пространства.

 

 

---

 

С. Якушко

ред. shtorm777.ru

ПОХОЖИЕ ЗАПИСИ

«Что такое четвертое измерение?» – Яндекс.Кью

Количеством измерений пространства удобно называть минимальное количество чисел, которые нужны, чтобы однозначно задать положение точки в этом пространстве. Тогда измерением будет одно из используемых нами чисел.
Возьмём, к примеру, лист бумаги. Очевидно, что чтобы задать положение любой точки на этом листе, необходимо минимум два числа. Мы условно выберем где-то начало, от которого мы будем отсчитывать числа, и затем любая точка будет характеризоваться расстоянием от начальной точки (по ширине и высоте). Значит, лист бумаги (а на самом деле его идеально бесконечно тонкая модель) — двумерное пространство.
Интуитивно понятно, что окружающий нас мир трёхмерен. Чтобы измерить габариты шкафа, нужно найти три числа, которые его характеризуют, — длину, ширину и высоту. Но иногда мы переставляем шкафы: вот шкаф в одном месте, а вот он в другом. Он поменял свои координаты. Можно сказать, что нам теперь нужно ещё одно число, чтобы однозначно задать положение шкафа в пространстве. В 10 часов утра шкаф стоял в комнате, а вечером он уже был на помойке.
Время — ещё одно число, а стало быть, измерение. До начала XX века при изучении природы мы в некотором смысле не уделяли времени особого значения. Всё изменилось с появлением Специальной Теории Относительности.
Мы поняли, что время не так уж сильно отличается от обычного пространства. Более того, оказывается, что время и пространство могут как бы превращаться друг в друга, переходить из одной формы в другую. Время может течь по-разному, пространство — сжиматься, и так далее.
Если мы возьмём двух близнецов и отправим одного из них в космическое путешествие на большой скорости, а второго оставим на Земле, то, вернувшись домой, путешественник увидит, что его брат стал стариком, в то время как сам он почти не изменился. Так происходит, потому что для человека, летящего на большой скорости, время течёт медленнее. Поэтому, если по часам космического корабля прошло пять лет, то на Земле — все пятьдесят.
В нынешнем представлении время и пространство неотделимы друг от друга, и поэтому в современной науке наш мир называется четырехмерным пространством-временем.

Почему мы живем в трехмерном пространстве | Futurist

Автор: Кристина Чернова |  5 мая 2016, 16:14

Мы живем в трехмерном мире: длина, ширина и глубина. Некоторые могут возразить: «А как же четвертое измерение — время?» Действительно, время — это тоже измерение. Но вот вопрос, почему пространство измеряется в трех измерениях — загадка для ученых. Новое исследование объясняет, почему мы живем в мире 3D.

Вопрос о том, почему пространство трехмерно, мучил ученых и философов с античных времен. Действительно, почему именно три измерения, а не десять или, скажем, 45?

В целом, пространство-время четырехмерно (или 3+1-мерно): три измерения образуют пространство, четвертым измерением является время. Существуют также философские и научные теории о многомерности времени, которые предполагают, что измерений времени на самом деле больше, чем кажется: привычная нам стрела времени, направленная из прошлого в будущее через настоящее — всего лишь одна из возможных осей. Это делает возможными различные научно-фантастические проекты, вроде путешествий во времени, а также создает новую, многовариантную космологию, которая допускает существование параллельных вселенных. Однако существование дополнительных временных измерений пока не доказано научно.

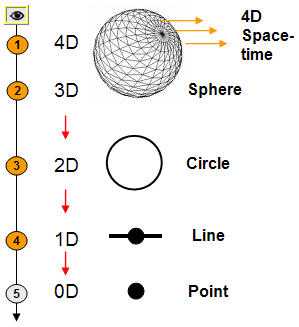
Вернемся в наше, 3+1-мерное измерение. Нам хорошо известно, что измерение времени связано со вторым законом термодинамики, который гласит, что в замкнутой системе — такой, как наша Вселенная — энтропия (мера хаоса) всегда возрастает. Уменьшаться вселенский беспорядок не может. Поэтому время всегда направлено вперед — и никак иначе.

В новой статье, опубликованной в EPL, исследователи предположили, что второй закон термодинамики может также объяснить, почему пространство трехмерно.

«Ряд исследователей в области науки и философии обращались к проблеме (3 + 1)-мерной природы пространства-времени, обосновывая выбор именно этого числа его стабильностью и возможностью поддержания жизни», — рассказал соавтор исследования Джулиан Гонсалес-Айала из Национального политехнического института в Мексике и университета Саламанки в Испании порталу Phys.org. «Ценность нашей работы заключается в том, что мы представляем рассуждения, основанные на физической модели размерности Вселенной с подходящим и разумным сценарием пространства-времени. Мы первые, кто заявил, что число «три» в размерности пространства возникает в качестве оптимизации физической величины».

Ранее ученые обращали внимание на размерность Вселенной в связи с так называемым атропным принципом: "Мы видим Вселенную такой, потому что только в такой Вселенной мог возникнуть наблюдатель, человек". Трехмерность пространства объяснялась возможностью поддержания Вселенной в том виде, в каком мы её наблюдаем. Если бы во Вселенной было множество измерений, по ньютоновскому закону тяготения не были бы возможны устойчивые орбиты планет и даже атомная структура вещества: электроны падали бы на ядра.

В данном исследовании ученые пошли другим путем. Они предположили, что пространство трехмерно из-за термодинамической величины — плотности свободной энергии Гельмгольца. Во Вселенной, заполненной излучением, эту плотность можно рассматривать как давление в пространстве. Давление зависит от температуры Вселенной и от количества пространственных измерений.

Исследователи показали, что могло происходить в первые доли секунды после Большого взрыва, называемые Планковской эпохой. В момент, когда Вселенная начала охлаждаться, плотность Гельмгольца достигла своего первого максимума. Тогда возраст Вселенной составлял долю секунды, а пространственных измерений было ровно три. Ключевая мысль исследования заключается в том, что трехмерное пространство было «заморожено», как только плотность Гельмгольца достигла своего максимального значения, которое запрещает переход в другие измерения.

На рисунке ниже изображено, как это происходило. Слева — плотность свободной энергии Гельмгольца (е) достигает своего максимального значения при температуре Т = 0,93, которое возникает, когда пространство было трехмерным (n=3). S и U представляют плотности энтропии и плотность внутренней энергии, соответственно. Справа показано, что перехода к многомерности не происходит при температуре ниже 0,93, что соответствует трем измерениям.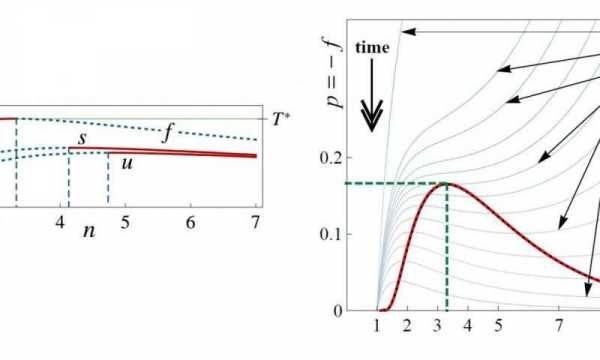

Это произошло вследствие второго закона термодинамики, который допускает переходы в более высокие измерения только тогда, когда температура выше критического значения — ни градусом меньше. Вселенная непрерывно расширяется, и элементарные частицы, фотоны, теряют энергию — поэтому наш мир постепенно охлаждается: Сейчас температура Вселенной гораздо ниже уровня, предполагающего переход из 3D-мира в многомерное пространство.

Исследователи поясняют, что пространственные измерения похожи на состояния вещества, а переход из одного измерения в другое напоминает фазовый переход — такой, как плавление льда, которое возможно лишь при очень высоких температурах.

«В процессе охлаждения ранней Вселенной и после достижения первой критической температуры, принцип приращения энтропии для замкнутых систем мог запретить определенные изменения размерности», — комментируют исследователи.

Это предположение по-прежнему оставляет место для более высоких измерений, которые существовали в Планковскую эпоху, когда Вселенная была еще более горячей, чем это было при критической температуре.

Дополнительные измерения присутствуют во многих космологических моделях — в первую очередь, в теории струн. Это исследование может помочь объяснить, почему в некоторых из этих моделей дополнительные измерения исчезли или остались такими же крошечными, как были в первые доли секунды после Большого взрыва, в то время как 3D-пространство продолжает расти во всей наблюдаемой Вселенной.

В будущем исследователи планируют улучшить свою модель, чтобы включить дополнительные квантовые эффекты, которые могли возникнуть в первую долю секунды после Большого взрыва. Кроме того, результаты дополненной модели могут также служить ориентиром для исследователей, работающих на других космологических моделях, таких как квантовая гравитация.

Понравилась статья?

Поделись с друзьями!

  Поделиться 0   Поделиться 0   Твитнуть 0

Подпишись на еженедельную рассылку

«Что такое четвертое измерение?» – Яндекс.Знатоки

Представить себе четырехмерное пространство или четветое измерение не так-то просто, но можно думать о том, что это пространство, в котором каждая точка задается четырьмя числами. На самом деле мы с вами действительно живем в четырехмерном пространстве-времени, потому что события нашей жизни кодируются как раз четырьмя числами — помимо положения в пространстве, есть еще и время.

Например, если вы назначаете свидание, то вы можете сделать это так: вы можете указать три числа, которые будут соответствовать точке в пространстве, и обязательно указать время, которое обычно задается в часах, минутах, секундах, но можно было бы закодировать его одним числом. Например, количество секунд, прошедших с определенной даты, — это тоже одно число. Таким образом получается четырехмерное пространство-время.

Представить себе геометрию этого четырехмерного пространства-времени не очень просто. Например, мы с вами привыкли к тому, что в нашем обычном трехмерном пространстве две плоскости могут пересекаться по прямой либо быть параллельными. Но не бывает такого, чтобы две плоскости пересекались в одной точке. Две прямые могут пересечься в одной точке, а на плоскости не могут в трехмерном пространстве. А в четырехмерном пространстве две плоскости могут и чаще всего пересекаются в одной точке.

Четырехмерное пространство нам важно, потому что оно применяется в физике, потому что мы в нем живем. А зачем нужны пространства более высоких измерений? Давайте представим себе, что мы изучаем какие-то объекты, которые обладают большим количеством параметров. Например, мы изучаем страны, и у каждой страны есть территория, количество населения, внутренний валовой продукт, количество городов, какие-нибудь коэффициенты, индексы, что-нибудь такое.

Мы можем представлять себе каждую страну в виде одной точки в каком-то пространстве достаточно высокой размерности. И оказывается, что с математической точки зрения это правильный способ об этом думать. В частности, переход к геометрии многомерного пространства позволяет анализировать разные сложные объекты, обладающие большим количеством параметров.

Подробнее в источнике: http://sneg5.com/nauka/fizika-i-matematika/mnogomernye-prostranstva-3d-4d.html

Многомерные пространства — 3D, 4D и другие измерения

Содержание Что такое четырёхмерное пространство («4D»)? Представление других измерений От 2D к 3D От 3D к 4D Что такое гиперкуб? Построение тессеракта Виды гиперкубов и их названия Как насчет 10D?

Многомерные пространства — миф или реальность? Большинству из нас, или, возможно, всем нам невозможно представить мир, состоящий из более чем трех пространственных измерений. Правильно ли утверждение, что такой мир не может существовать? Или просто человеческий разум не способен вообразить дополнительные измерения — измерения, которые могут оказаться такими же реальными, как и другие вещи, которые мы не можем увидеть?

Мы достаточно часто слышим что-нибудь вроде «трехмерное пространство», или «многомерное пространство», или «четырехмерное пространство». Возможно, вы знаете, что мы живем в четырехмерном пространстве-времени. Что это означает и почему это интересно, почему математики и не только математики изучают такие пространства?

Об авторах Илья Щуров — кандидат физико-математических наук, доцент кафедры высшей математики НИУ ВШЭ. Jason Hise — Physics programmer at Ready at Dawn Studios, 4D geometry enthusiast. Автор анимированных моделей, представленных в данной статье. ashgrowen — пикабушник, проиллюстрировавший в этой статье построение тессеракта и гиперкуба.

Давайте начнем с простого — начнем с одномерного пространства. Представим себе, что у нас есть город, который расположен вдоль дороги, и в этом городе есть только одна улица. Тогда мы можем каждый дом на этой улице закодировать одним числом — у дома есть номер, и этот номер однозначно определяет, какой дом имеется в виду. Люди, которые живут в таком городе, — можно считать, что они живут в таком одномерном пространстве. Жить в одномерном пространстве довольно скучно, и люди обычно живут не в одномерном пространстве.

Например, если мы говорим про города, то можно перейти от одномерного пространства к двумерному. Примером двумерного пространства является плоскость, а если мы продолжим нашу аналогию с городами, то это город, в котором можно расчертить улицы, допустим, перпендикулярно друг другу, как это сделано в Нью-Йорке, в центре Нью-Йорка. Там есть «стрит» и авеню, каждая из которых имеет свой номер, и вы можете задавать местоположение на плоскости, задавать два числа. Опять же, все мы знаем декартову систему координат, знакомую со школы, — каждая точка задается двумя числами. Это пример двумерного пространства.

Но если мы говорим про город типа центра Нью-Йорка, то на самом деле он является трехмерным пространством, потому что вам мало задать, например, конкретный дом, пусть даже вы зададите его пересечением какой-нибудь «стрит» и какой-нибудь авеню, — вам нужно будет задать еще и этаж, на котором находится нужная вам квартира. Это даст вам третье измерение — высоту. У вас получится трехмерное пространство, в котором каждая точка задается тремя числами.

Вопрос: что такое четырехмерное пространство? Представить его себе не так-то просто, но можно думать о том, что это пространство, в котором каждая точка задается четырьмя числами. На самом деле мы с вами действительно живем в четырехмерном пространстве-времени, потому что события нашей жизни кодируются как раз четырьмя числами — помимо положения в пространстве, есть еще и время. Например, если вы назначаете свидание, то вы можете сделать это так: вы можете указать три числа, которые будут соответствовать точке в пространстве, и обязательно указать время, которое обычно задается в часах, минутах, секундах, но можно было бы закодировать его одним числом. Например, количество секунд, прошедших с определенной даты, — это тоже одно число. Таким образом получается четырехмерное пространство-время.

Представить себе геометрию этого четырехмерного пространства-времени не очень просто. Например, мы с вами привыкли к тому, что в нашем обычном трехмерном пространстве две плоскости могут пересекаться по прямой либо быть параллельными. Но не бывает такого, чтобы две плоскости пересекались в одной точке. Две прямые могут пересечься в одной точке, а на плоскости не могут в трехмерном пространстве. А в четырехмерном пространстве две плоскости могут и чаще всего пересекаются в одной точке. Можно представлять себе, хотя это уже совсем сложно, пространство большей размерности. На самом деле математики, когда работают с пространствами высокой размерности, чаще всего говорят просто: допустим, пятимерное пространство — это пространство, в котором точка задается пятью числами, пятью координатами. Безусловно, математики разработали разные методы, которые позволяют понимать что-то о геометрии такого пространства.

Почему это важно? Зачем понадобились такие пространства? Во-первых, четырехмерное пространство нам важно, потому что оно применяется в физике, потому что мы в нем живем. А зачем нужны пространства более высоких измерений? Давайте представим себе, что мы изучаем какие-то объекты, которые обладают большим количеством параметров. Например, мы изучаем страны, и у каждой страны есть территория, количество населения, внутренний валовой продукт, количество городов, какие-нибудь коэффициенты, индексы, что-нибудь такое. Мы можем представлять себе каждую страну в виде одной точки в каком-то пространстве достаточно высокой размерности. И оказывается, что с математической точки зрения это правильный способ об этом думать.

В частности, переход к геометрии многомерного пространства позволяет анализировать разные сложные объекты, обладающие большим количеством параметров.

Для того чтобы изучать такие объекты, используются методы, разработанные в науке, которая называется линейная алгебра. Несмотря на то, что она алгебра, на самом деле это наука о геометрии многомерных пространств. Конечно, поскольку представить их себе довольно тяжело, математики используют формулы, для того чтобы как раз изучать такие пространства.

Представить себе четырех-, пяти- или шестимерное пространство довольно сложно, но математики не боятся трудностей, и им мало даже стомерных пространств. Математики придумали бесконечномерное пространство — пространство, содержащее бесконечное количество измерений. В качестве примера такого пространства можно привести пространство всех возможных функций, заданных на отрезке или прямой.

Оказывается, что методы, которые были разработаны для конечномерных пространств, во многом переносятся и на случаи чрезвычайно сложных с точки зрения просто попытки их все представить пространств.

У линейной алгебры есть многочисленные приложения не только в математике, но и в самых разных науках, начиная c физики и заканчивая, например, экономикой или политической наукой. В частности, линейная алгебра является основой для многомерной статистики, которая как раз используется для вычленения связей между различными параметрами в каких-то массивах данных. В частности, популярный ныне термин Big Data зачастую связывается с решением задач по обработке данных, которые представляются именно большим количеством точек в пространстве какой-то конечной размерности. Чаще всего такие задачи можно переформулировать и разумно воспринимать именно в геометрических терминах.

Со школьных лет математика разделяется на алгебру и геометрию. Но на самом деле, если мы задумаемся о том, как устроена современная математика, то мы поймем, что те задачи, которые сейчас решаются, в частности, с применением методов линейной алгебры, на самом деле являются очень отдаленным продолжением тех задач, над которыми задумывались многие тысячи лет назад, например Пифагор или Евклид, разрабатывая ту самую школьную геометрию, которая сейчас есть в любом школьном учебнике. Удивительно, что задача по анализу больших данных оказывается в некотором смысле потомком, казалось бы, совсем бессмысленных — по крайней мере с практической точки зрения — упражнений древних греков по рисованию прямых или окружностей на плоскости или мысленному проведению прямых или плоскостей в трехмерном пространстве.

Что такое четырёхмерное пространство («4D»)?

Тессерракт — четырехмерный куб

Всем знакомо сокращение 3D, означающее «трёхмерный» (буква D — от слова dimension — измерение). Например, выбирая в кинотеатре фильм с пометкой 3D, мы точно знаем: для просмотра придётся надеть специальные очки, но зато картинка будет не плоской, а объёмной. А что такое 4D? Существует ли «четырёхмерное пространство» в реальности? И можно ли выйти в «четвёртое измерение»?

Чтобы ответить на эти вопросы, начнём с самого простого геометрического объекта — точки. Точка нульмерна. У неё нет ни длины, ни ширины, ни высоты.

Сдвинем теперь точку по прямой на некоторое расстояние. Допустим, что наша точка — остриё карандаша; когда мы её сдвинули, она прочертила отрезок. У отрезка есть длина, и больше никаких измерений: он одномерен. Отрезок «живёт» на прямой; прямая является одномерным пространством.

Тессеракт — четырехмерный куб

Возьмём теперь отрезок и попробуем его сдвинуть так, как раньше точку. Можно представить себе, что наш отрезок — это основание широкой и очень тонкой кисти. Если мы выйдем за пределы прямой и будем двигаться в перпендикулярном направлении, получится прямоугольник. У прямоугольника есть два измерения — ширина и высота. Прямоугольник лежит в некоторой плоскости. Плоскость — это двумерное пространство (2D), на ней можно ввести двумерную систему координат — каждой точке будет соответствовать пара чисел. (Например, декартова система координат на школьной доске или широта и долгота на географической карте.).

Если сдвинуть прямоугольник в направлении, перпендикулярном плоскости, в которой он лежит, получится «кирпичик» (прямоугольный параллелепипед) — трёхмерный объект, у которого есть длина, ширина и высота; он расположен в трёхмерном пространстве, в таком, в каком живём мы с вами. Поэтому мы хорошо представляем себе, как выглядят трёхмерные объекты. Но если бы мы жили в двумерном пространстве — на плоскости, — нам пришлось бы изрядно напрячь воображение, чтобы представить себе, как можно сдвинуть прямоугольник, чтобы он вышел из той плоскости, в которой мы живём.

Тессеракт — четырехмерный куб

Представить себе четырёхмерное пространство для нас также довольно непросто, хотя очень легко описать математически. Трёхмерное пространство — это пространство, в котором положение точки задаётся тремя числами (например, положение самолёта задаётся долготой, широтой и высотой над уровнем моря). В четырёхмерном же пространстве точке соответствует четвёрка чисел-координат. «Четырёхмерный кирпич» получается сдвигом обычного кирпичика вдоль какого-то направления, не лежащего в нашем трёхмерном пространстве; он имеет четыре измерения.

На самом деле мы сталкиваемся с четырёхмерным пространством ежедневно: например, назначая свидание, мы указываем не только место встречи (его можно задать тройкой чисел), но и время (его можно задавать одним числом, например количеством секунд, прошедших с определенной даты). Если посмотреть на настоящий кирпич, у него есть не только длина, ширина и высота, но ещё и протяженность во времени — от момента создания до момента разрушения.

Физик скажет, что мы живём не просто в пространстве, а в пространстве-времени; математик добавит, что оно четырёхмерно. Так что четвёртое измерение ближе, чем кажется.

 

Представление других измерений

 

От 2D к 3D

Ранняя попытка объяснить концепцию дополнительных измерений появилась в 1884 году с публикацией романа о плоской земле Эдвина А. Эббота «Флатландия: романтика множества измерений«.  Действие в романе разворачивается в плоском мире, называемом «Флатландия», а повествование ведется от лица жителя этого мира — квадрата. Однажды во сне квадрат оказывается в одномерном мире — Лайнландии, жители которой (треугольники и другие двумерные объекты представлены в виде линий) и пытается объяснить правителю этого мира существование 2-го измерения, однако, приходит к выводу о том, что его невозможно заставить выйти за рамки мышления и представления только прямых линий.

Квадрат описывает его мир как плоскость, населенную линиями, кругами, квадратами, треугольниками и пятиугольниками.

Сфера, с точки зрения Квадрата — Окружность. │ commons.wikimedia.org

Однажды перед квадратом появляется шар, но его суть он не может постичь, так как квадрат в своем мире может видеть только срез сферы, только форму двумерного круга.

Сфера пытается объяснить квадрату устройство трехмерного мира, но квадрат понимает только понятия «вверх/вниз» и «лево/право», он не способен постичь понятия «вперед/назад».

Непостижимая Квадратом тайна третьего измерения на примере прохождения сферы через плоскость. Герой наблюдает уменьшение Окружности до точки и её исчезновение. │ commons.wikimedia.org

Только после того, как сфера вытащит квадрат из его двумерного мира в свой трехмерный мир, он наконец поймет концепцию трех измерений. С этой новой точки зрения квадрат становится способен видеть формы своих соотечественников.

Квадрат, вооруженный своим новым знанием, начинает осознавать возможность существования четвертого измерения. Также он приходит к мысли, что число пространственных измерений не может быть ограничено. Стремясь убедить сферу в этой возможности, квадрат использует ту же логику, что и сфера, аргументирующая существование трех измерений. Но теперь из них двоих становится «близорукой» сфера, которая не может понять этого и не принимает аргументы и доводы квадрата — так же, как большинство из нас «сфер» сегодня не принимают идею дополнительных измерений.

Рецензия на книгу Флатландия Принимая во внимание исключительность как жанра, который при некоторой фантазии и существовании иных его представителей, можно было бы назвать математическим романом, так и самой книги, её не хочется сильно ругать. Тем не менее, похвалы здесь заслуживает только лишь непривычность подачи, по духу близкая произведениям Льюиса Керрола, однако, в отличие от него, имеющая гораздо меньше точек соприкосновения с реальной жизнью. Данная книга, как верно отмечено в предисловии к изданию, не похожа ни на одну популяризацию, читателю, однако, не вполне ясно, по какой причине её сравнивают с популяризациями, потому как, хотя математические истины в ней, безусловно, затрагиваются, какой бы то ни было популяризацией книгу определённо считать невозможно. И вот почему: Перед вами уникальный пример объединения художественного вымысла с математическими идеями. И поклоннику математики, любящему читать, задумка изначально кажется замечательной: подобно математическим постулатам, ввести в рассмотрение ряд абстрактных объектов, наделить их определёнными свойствами, задать правила игры в описанном пространстве, а после, подражая опять же мысли исследователя, наблюдающего взаимодействия этих умозрительных объектов, проследить за их трансформацией. Но, так как книга всё же художественная, усилиям воли учёного места здесь не находится, поэтому для самодостаточности представленного на всеобщее обозрение мира объекты здесь наделяются сознанием и мотивацией для каких-либо взаимодействий друг с другом, после чего в прежде абстрактный мир оторванных от повседневной жизни чистых идей приносятся социальные взаимодействия с целым ворохом проблем, всегда сопутствующих всяким взаимоотношениям. Всевозможные трения, возникающие в книге на социальной почве, по мнению зрителя совершенно не нужны в книге: они практически не раскрыты и не могут восприниматься в серьезе, и в то же время отвлекают читателя от истинно тех вещей, ради которых написана книга. Даже принимая во внимания заверения обоих авторов о неспешности повествования, якобы более комфортную для читателя при приобретении каких-либо знаний (именно здесь приводится сравнение с популяризациями), зрителю темп повествования показался чрезвычайно затянутым и медлительным, а повторение одного и того же объяснения по несколько раз одними и теми же словами заставило усомниться в том, что рассказчик адекватно оценивает его умственным способности. И в конечном счёте неясно, для кого эта книга. Непривычным к математике людям описание в общем-то интересных явление в столь вольной форме вряд ли принесёт удовольствие, знакомым же с математикой ближе будет гораздо приятнее взять в руки качественную популяризацию, где величие и красоту математики не разбавляют плоскими сказками.

От 3D к 4D

Нам сложно принять эту идею, потому что, когда мы пытаемся представить даже одно дополнительное пространственное измерение — мы упираемся в кирпичную стену понимания. Похоже, что наш разум не может выйти за эти границы.

Представьте себе, например, что вы находитесь в центре пустой сферы. Расстояние между вами и каждой точкой на поверхности сферы равно. Теперь попробуйте двигаться в направлении, которое позволяет вам отойти от всех точек на поверхности сферы, сохраняя при этом равноудаленность. Вы не сможете этого сделать..

Житель Флатландии столкнулся бы с такой же проблемой, если бы он находился в центре круга. В его двумерном мире он не может находиться в центре круга и двигаться в направлении, которое позволяет ему оставаться равноудаленными каждой точке окружности круга, если только он не перейдет в третье измерение. Увы, у нас нет проводника в четырехмерное пространство как в романе Эббота, чтобы показать нам путь к 4D.

Что такое гиперкуб? Построение тессеракта

Виды гиперкубов и их названия 1. Точка — нулевое измерение 2. Отрезок — одномерное пространство 3. Квадрат — двумерное пространство (2D) 4. Куб — трёхмерное пространство (3D) 5. Тессеракт — четырёхмерное пространство (4D) 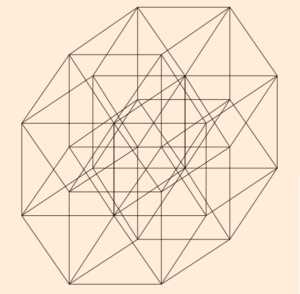6. Пентеракт — пятимерное пространство (5D) 7. Хексеракт — шестимерное пространство (6D) 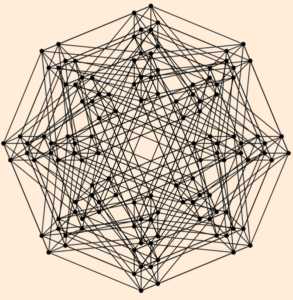8. Хептеракт — семимерное пространство (7D) 9. Октеракт — восьмимерное пространство (8D) 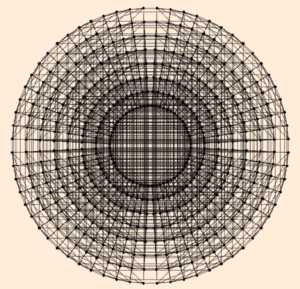10. Энтенеракт — девятимерное пространство (9D) 11. Декеракт — десятимерное пространство (10D)

Гиперкуб — это обобщающее название куба в производном числе измерений. Всего измерений десять, плюс точка (нулевое измерение).

Соответственно, существует одиннадцать видов гиперкуба. Рассмотрим построение тессеракта — гиперкуба четвертого измерения:

Для начала построим точку А (рис. 1):

Рис. 1 Точка

После, соединим ее с точкой В. Получим вектор АВ (рис. 2):

Рис. 2 Вектор

Построим вектор, параллельный вектору АВ, и назовем его CD. Соединив начала и концы векторов, получим квадрат ABDC (рис. 3):

Рис. 3 Квадрат

Теперь построим еще один квадрат A1B1D1C1, который лежит в параллельной плоскости. Соединив точки подобным образом, получим куб (рис. 4):

Рис. 4 Куб

У нас есть куб. Представьте, что положение куба в трехмерном пространстве с течением времени изменилось. Зафиксируем его новое местоположение (рис 5.):

Рис. 5 Измененное положение куба в пространстве

А теперь, мы проводим вектора, которые соединяют местоположение точек в прошлом и в настоящем. Получаем тессеракт (рис. 6):

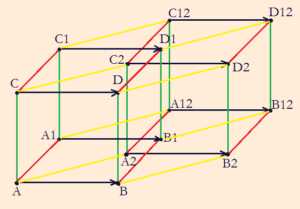
Рис. 6 Тессеракт (построение)

Подобным образом строятся остальные гиперкубы, конечно же учитывается смысл пространства, в котором гиперкуб находится.

 

Как насчет 10D?

В 1919 году польский математик Теодор Калуца предположил, что существование четвертого пространственного измерения может увязать между собой общую теорию относительности и электромагнитную теорию. Идея, впоследствии усовершенствованная шведским математиком Оскаром Кляйном, заключалась в том, что пространство состояло как из «расширенных» измерений, так и из «свернутых» измерений. Расширенные измерения — это три пространственных измерения, с которыми мы знакомы, и свернутое измерение находится глубоко в расширенных размерах. Эксперименты позже показали, что свернутое измерение Калуцы и Кляйна не объединило общую теорию относительности и электромагнитную теорию, как это первоначально предполагалось, но спустя десятилетия теоретики теории струн нашли эту идею полезной, даже необходимой.

Математика, используемая в теории суперструн, требует не менее 10 измерений. То есть для уравнений, описывающих теорию суперструн и для того чтобы связать общую теорию относительности с квантовой механикой, для объяснения природы частиц, для объединения сил и т. д. — необходимо использовать дополнительные измерения. Эти измерения, по мнению теоретиков струн, завернуты в свернутое пространство, изначально описанное Калуцей и Кляйном.

Круги представляют собой дополнительный пространственный размер, свернутый в каждую точку нашего знакомого трехмерного пространства. │ WGBH / NOVA

Чтобы расширить скрученное пространство, чтобы включить эти добавленные размеры, представьте, что круги Калуцы-Клейна заменяются сферами. Вместо одного добавленного измерения мы имеем два, если рассматривать только поверхности сфер и три, если учесть пространство внутри сферы. Получилось всего шесть измерений. Так где же другие, которые требует теория суперструн?

Оказывается, что до того, как появилась теория суперструн, два математика Эудженио Калаби из Университета Пенсильвании и Шин-Тунг Яу из Гарвардского университета описали шестимерные геометрические формы. Если мы заменим сферы в скрученном пространстве этими формами Калаби-Яу, мы получим 10 измерений: три пространственных, а также шестимерные фигуры Калаби-Яу.

Шестимерные формы Калаби-Яу могут объяснять дополнительные размеры, требуемые теорией суперструн. │ WGBH / NOVА

Приверженцы теории струн делают ставку на то, что дополнительные измерения действительно существуют. На самом деле, уравнения, описывающие теорию суперструн, предполагают вселенную с не менее чем 10 измерениями. Но даже физикам, которые все время думают о дополнительных пространственных измерениях сложно описать как они могут выглядеть, или как люди могли бы приблизиться к их пониманию.

Если теория суперструн будет доказана и идея мира, состоящего из 10 или более измерений, подтвердится, то появится ли когда-нибудь объяснение или визуальное представление более высоких измерений, которые сможет постичь человеческий разум? Ответ на этот вопрос навсегда может стать отрицательным, если только какая-то четырехмерная жизненная форма не «вытащит» нас из нашего трехмерного мира и не даст нам увидеть мир с ее точки зрения.

 

---

 

Сохранить

Сохранить

Сохранить

Сохранить

Сохранить

Сохранить

Сохранить

Сохранить

Сохранить

Общая оценка материала: 4.8

Оценка незарегистрированных пользователей:

[Total: 26 Average: 4.9]

Тессеракт — Википедия

Анимированная проекция вращающегося тессеракта

Тессера́кт (от др.-греч. τέσσαρες ἀκτῖνες — «четыре луча») — четырёхмерный гиперкуб, аналог обычного трёхмерного куба в четырёхмерном пространстве. Другие названия: 4-куб, тетраку́б, восьмияче́йник^[1], октахо́р (от др.-греч. οκτώ «восемь» + χώρος «место, пространство»), гиперкуб (если число измерений не оговаривается).

Согласно Оксфордскому словарю, слово «тессеракт» было придумано Чарльзом Говардом Хинтоном^[en] (1853—1907) и впервые использовано в 1888 году в его книге «Новая эра мысли».

Обычный тессеракт в евклидовом четырёхмерном пространстве определяется как выпуклая оболочка точек (±1, ±1, ±1, ±1). Иначе говоря, он может быть представлен в виде следующего множества:

[−1,1]4≡{(x1,x2,x3,x4):−1≤xi≤1}.{\displaystyle [-1,1]^{4}\equiv \{(x_{1},x_{2},x_{3},x_{4})\,:\,-1\leq x_{i}\leq 1\}.}

Тессеракт ограничен восемью гиперплоскостями xi=±1,i=1,2,3,4{\displaystyle x_{i}=\pm 1,\;i=1,2,3,4}, пересечение которых с самим тессерактом задаёт его трёхмерные грани (являющиеся обычными кубами). Каждая пара непараллельных трёхмерных граней пересекается, образуя двумерные грани (квадраты), и так далее. Окончательно, тессеракт обладает 8 трёхмерными гранями, 24 двумерными, 32 рёбрами и 16 вершинами.

Четырёхмерный гиперобъём тессеракта со стороной длиной a рассчитывается по формуле:
V4=a4{\displaystyle V_{4}=a^{4}}

Объём же гиперповерхности тессеракта можно найти по формуле:
V3(hypersurface)=8a3{\displaystyle V_{3}({\text{hypersurface}})=8a^{3}}

Радиус описанной гиперсферы:
R=a{\displaystyle R=a}

Радиус вписанной гиперсферы:
r=a2{\displaystyle r={\frac {a}{2}}}

Попытаемся представить себе, как будет выглядеть гиперкуб, не выходя из трёхмерного пространства.

В одномерном «пространстве» — на линии — выделим отрезок АВ длиной L. На двумерной плоскости на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат CDBA. Повторив эту операцию с плоскостью, получим трёхмерный куб CDBAGHFE. А сдвинув куб в четвёртом измерении (перпендикулярно первым трём) на расстояние L, мы получим гиперкуб CDBAGHFEKLJIOPNM.

Построение тессеракта на плоскости

Развёртка тессеракта

Одномерный отрезок АВ служит стороной двумерного квадрата CDBA, квадрат — стороной куба CDBAGHFE, который, в свою очередь, будет стороной четырёхмерного гиперкуба. Отрезок прямой имеет две граничные точки, квадрат — четыре вершины, куб — восемь. В четырёхмерном гиперкубе, таким образом, окажется 16 вершин: 8 вершин исходного куба и 8 сдвинутого в четвёртом измерении. Он имеет 32 ребра — по 12 дают начальное и конечное положения исходного куба, и ещё 8 рёбер «нарисуют» восемь его вершин, переместившихся в четвёртое измерение. Те же рассуждения можно проделать и для граней гиперкуба. В двумерном пространстве она одна (сам квадрат), у куба их 6 (по две грани от переместившегося квадрата и ещё четыре опишут его стороны). Четырёхмерный гиперкуб имеет 24 квадратные грани — 12 квадратов исходного куба в двух положениях и 12 квадратов от двенадцати его рёбер.

Как сторонами квадрата являются 4 одномерных отрезка, а сторонами (гранями) куба являются 6 двухмерных квадратов, так и для «четырёхмерного куба» (тессеракта) сторонами являются 8 трёхмерных кубов. Пространства противоположных пар кубов тессеракта (то есть трёхмерные пространства, которым эти кубы принадлежат) параллельны. На рисунке это кубы: CDBAGHFE и KLJIOPNM, CDBAKLJI и GHFEOPNM, EFBAMNJI и GHDCOPLK, CKIAGOME и DLJBHPNF.

Аналогичным образом можно продолжить рассуждения для гиперкубов большего числа измерений, но гораздо интереснее посмотреть, как для нас, жителей трёхмерного пространства, будет выглядеть четырёхмерный гиперкуб. Воспользуемся для этого уже знакомым методом аналогий.

Возьмём проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединённые четырьмя линиями — боковыми рёбрами. Аналогичным образом четырёхмерный гиперкуб в пространстве трёх измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединённых восемью рёбрами. При этом сами «ящики» — трёхмерные грани — будут проецироваться на «наше» пространство, а линии, их соединяющие, протянутся в направлении четвёртой оси. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.

Подобно тому, как трёхмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвёртое измерение, сформирует гиперкуб. Его ограничивают восемь кубов, которые в перспективе будут выглядеть как некая довольно сложная фигура. Сам же четырёхмерный гиперкуб состоит из бесконечного количества кубов, подобно тому как трёхмерный куб можно «нарезать» на бесконечное количество плоских квадратов.

Разрезав шесть граней трёхмерного куба, можно разложить его в плоскую фигуру — развёртку. Она будет иметь по квадрату с каждой стороны исходной грани плюс ещё один — грань, ей противоположную. А трёхмерная развёртка четырёхмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс ещё одного — конечной «гиперграни».

Свойства тессеракта представляют собой продолжение свойств геометрических фигур меньшей размерности в четырёхмерное пространство.

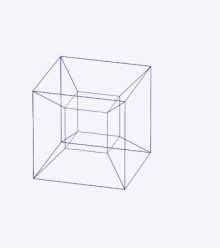Разворачивание поверхности тессеракта в трёхмерное пространство

Аналогично тому, как поверхность куба может быть развёрнута в многоугольник, состоящий из шести квадратов, поверхность тессеракта может быть развёрнута в трёхмерное тело, состоящее из восьми кубов^[2].

Существует 261 развёртка тессеракта^[3]. Развёртки гиперкуба могут быть найдены перечислением «сдвоенных деревьев», где «сдвоенное дерево» (paired tree) — это дерево с чётным числом вершин, которые разбиты на пары так, что ни одна пара не состоит из двух смежных вершин. Между «сдвоенными деревьями» с 8 вершинами и развёртками тессеракта существует взаимно однозначное соответствие. Всего существует 23 дерева с 8 вершинами, при разбиении вершин которых на пары несмежных вершин получается 261 «сдвоенное дерево» с 8 вершинами^[4].

Крестообразная развёртка тессеракта является элементом картины Сальвадора Дали «Corpus Hypercubus» (1954)^[5].

В рассказе Роберта Хайнлайна «Дом, который построил Тил» калифорнийский архитектор Квинтус Тил строит дом в форме развёртки гиперкуба, который во время землетрясения складывается в четырёхмерный тессеракт^[5].

На двумерное пространство[править | править код]

Данная структура сложна для воображения, но возможно спроецировать тессеракт в двумерные или трёхмерные пространства. Кроме того, проецирование на плоскость позволяет легко понять расположение вершин гиперкуба. Таким образом, можно получить изображения, которые больше не отражают пространственные отношения в пределах тессеракта, но которые иллюстрируют структуру связи вершин, как в предыдущих примерах:

Первая картинка показывает, как тессеракт получен в результате комбинирования двух кубов. Схема подобна построению куба от двух квадратов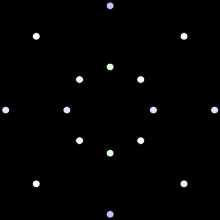

Вторая картинка иллюстрирует тот факт, что все рёбра тессеракта имеют одинаковую длину. Она примечательна тем, что все восемь кубов имеют одинаковый вид.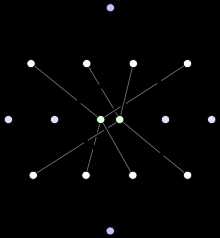

Третья картинка демонстрирует тессеракт в изометрии, относительно точки построения. Это изображение представляет интерес при использовании тессеракта как основания для топологической сети, чтобы связать многократные процессоры в параллельных вычислениях.

На трёхмерное пространство[править | править код]

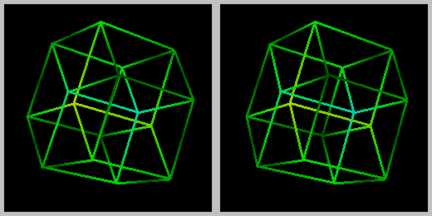
Вращающаяся модель тессеракта. Эта модель показывает грани тессеракта — равные кубы

Одна из проекций тессеракта на трёхмерное пространство представляет собой два вложенных трёхмерных куба, соответствующие вершины которых соединены между собой отрезками. Внутренний и внешний кубы имеют разные размеры в трёхмерном пространстве, но в четырёхмерном пространстве это равные кубы. Для понимания равности всех кубов тессеракта была создана вращающаяся модель тессеракта.

• Шесть усечённых пирамид по краям тессеракта — это изображения равных шести кубов. Однако эти кубы для тессеракта — как квадраты (грани) для куба. Но на самом деле тессеракт можно разделить на бесконечное количество кубов, как куб — на бесконечное количество квадратов, или квадрат — на бесконечное число отрезков.

Ещё одна интересная проекция тессеракта на трёхмерное пространство представляет собой ромбододекаэдр с проведёнными четырьмя его диагоналями, соединяющими пары противоположных вершин при больших углах ромбов. При этом 14 из 16 вершин тессеракта проецируются в 14 вершин ромбододекаэдра, а проекции 2 оставшихся совпадают в его центре. В такой проекции на трёхмерное пространство сохраняются равенство и параллельность всех одномерных, двухмерных и трёхмерных сторон.

Стереопара[править | править код]

Стереопара тессеракта изображается как две проекции на плоскость одного из вариантов трёхмерного представления тессеракта. Стереопара рассматривается так, чтобы каждый глаз видел только одно из этих изображений, возникает стереоскопический эффект, позволяющий лучше воспринять проекцию тессеракта на трёхмерное пространство.

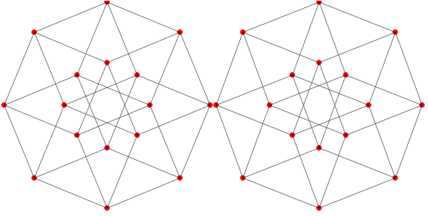
• В рассказе «Дом, который построил Тил» (в другом варианте перевода «И построил он себе скрюченный домишко») Хайнлайна описан восьмикомнатный дом в форме развёрнутого тессеракта.
• Рассказ Генри Каттнера «Все тенали бороговы» описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт.
• В рассказе Роберта Шекли «Мисс Мышка и четвёртое измерение» писатель-эзотерик, знакомец автора, пытается увидеть тессеракт, часами глядя на сконструированный им прибор: шар на ножке с воткнутыми в него стержнями, на которые насажены кубы, обклеенные всеми подряд эзотерическими символами. В рассказе упоминается труд Хинтона.
• В фантастическом рассказе Марка Клифтона «На ленте Мёбиуса» дети-вундеркинды путешествуют через пространство и время, используя модели ленты Мёбиуса, бутылки Клейна и тессеракта.
• Во Вселенной Marvel тессеракт является артефактом-носителем одного из шести Камней Бесконечности.
• В фильме «Интерстéллар» (англ. Interstellar) герой Мэттью Макконахи космонавт НАСА Купер пересекает горизонт событий и падает в чёрную дыру. После катапультирования из космического аппарата он попадает в тессеракт.

1. ↑ Д. К. Бобылёв. Четырехмерное пространство // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
2. ↑ Gardner, 1989, pp. 48—50.
3. ↑ Gardner, 1989, p. 272: «Peter Turney, in his 1984 paper „Unfolding the Tesseract“, uses graph theory to show that there are 261 distinct unfoldings.».
4. ↑ Peter Turney. Unfolding the Tesseract (англ.) // Journal of Recreational Mathematics : journal. — 1984-85. — Vol. 17, no. 1.
5. ↑ ^{1 2} Gardner, 1989, p. 50.

На русском языке

На английском языке

Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

Как легко понять четырехмерное пространство (17 фото)

Из моего опыта вживую, надо начать с 2-х мерного пространства, подготовить мозг. Поэтому берем несчастных 2-мерных существ, живущих в 2-мерном мире, на плоскости. В Плоском мире )) Как им понять наш трехмерный мир? А очень просто.

Вот это — квадрат, фигура, хорошо знакомая плоскостникам.

А вот фигура, несколько странная и непонятная плоскостникам

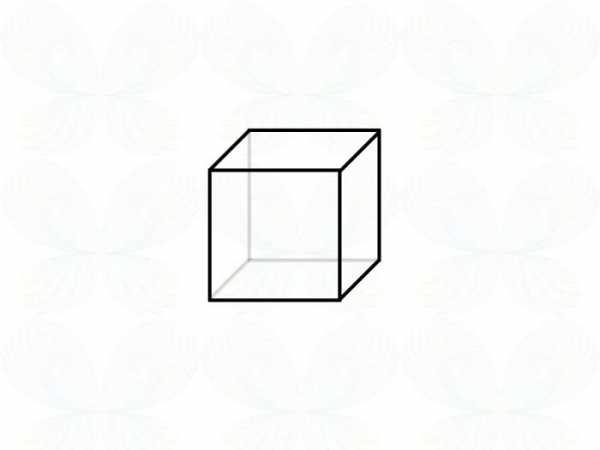
Мы с вами, жители трехмерного мира, легко узнаем в ней куб, составленный из квадратов. Хотя бы еще не выходили из плоскости, но мы, трехмерники, ясно понимаем: куб, че тут еще думать )))

Однако жители двумерного мира, не умеющие мыслить как мы, тремя измерениями, видят в ней другие фигуры, с их точки зрения:

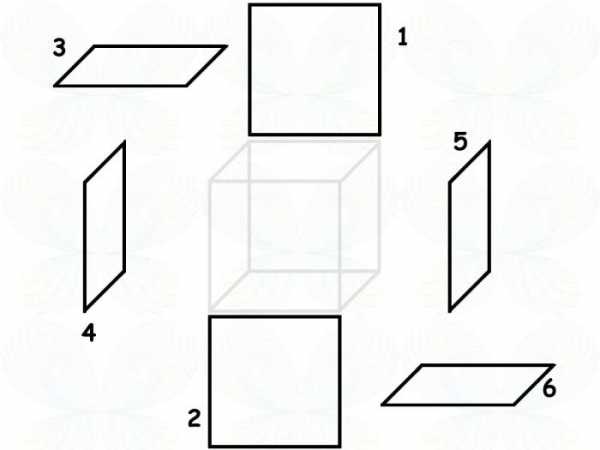
Из коих только 1 и 2 — квадраты, а остальные — нечто перекошенное. С некоторой натяжкой плоскостники могут сказать, что фигуры 3, 4, 5 и 6 — это перекошенные квадратики. Вот это важный момент.

Это переход от двумерного мышления — к нашему трехмерному. Что вы видите на следующей картинке? Там разные фигуры — или все одни и те же, квадратики, просто в разных проекциях?

Мы, трехмерники, спокойно можем сказать, что это все — квадраты. И плоскостник, умеющий мыслить на одно измерение больше — может сказать то же самое. Что это проекции квадратов в его плоское измерение. Хотя все его двумерные сотоварищи будут видеть трапеции и только два квадрата.

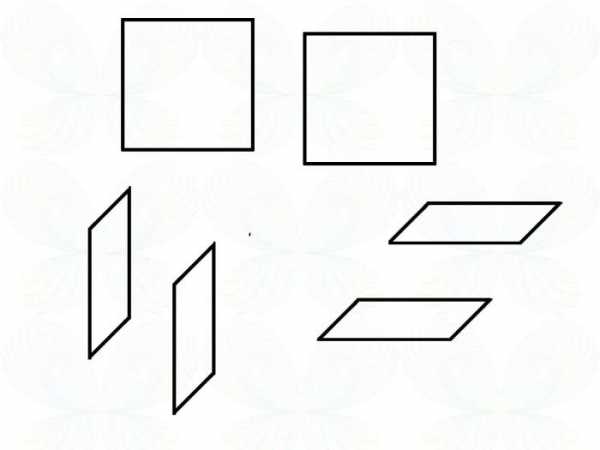
Все, закончили с плоскостниками, возвращаемся в наше, трехмерное измерение.

Обычный куб я вам показывать не буду, покажу сразу: 4-х мерный куб )) Он еще носит название «тессеракт» или «гиперкуб». Это вот такая штука:

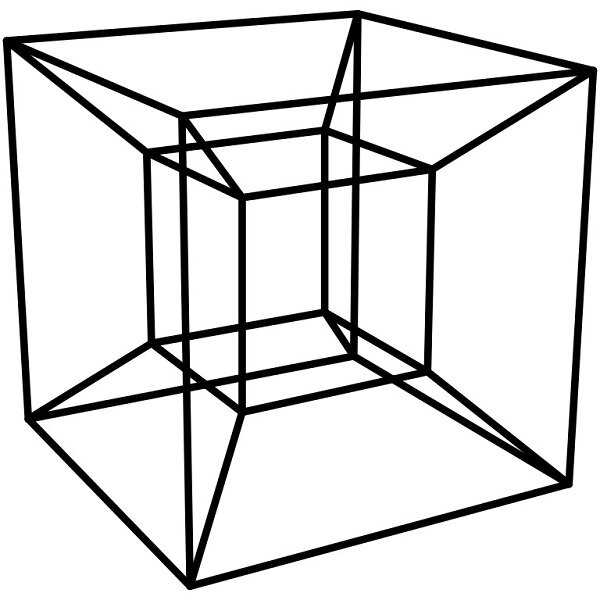
Чтобы легче его представить, вот он в других разных видах:

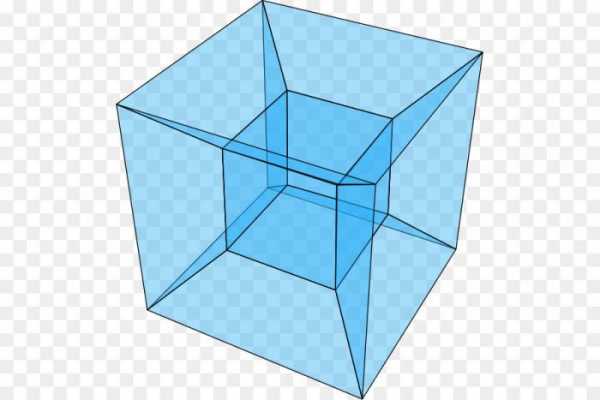
Представьте, что вы такое держите в руках. Я делал такие штуки из разных материалов, это не сложно

Что вы здесь видите? Кубик, к которому присоединены шесть призм? Ну, это если мы будем думать по нашему, по трехмерному. А если думать по четырехмерному, на одно измерение больше, то это 8 (восемь) кубов!

Восемь кубиков, соединенных гранями. Просто шесть из них искажены в призмы, так как наше пространство 3-мерное, а этот объект — 4-мерный. Тессеракт это 4-мерный куб. Гиперкуб. Все просто )))

Вернемся на секунду к плоскому миру, с меньшим числом измерений, чем у нас.

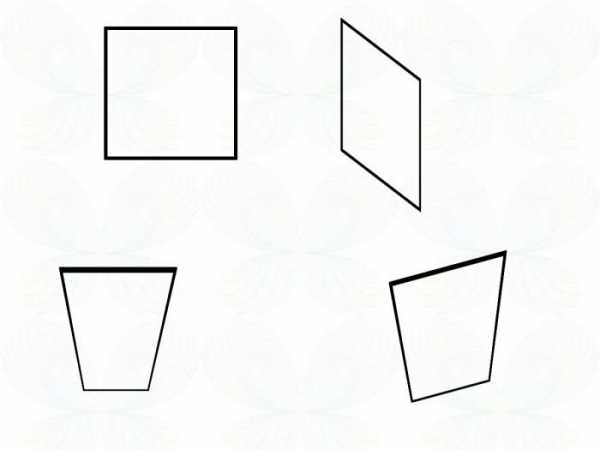
С точки зрения двумерников (у них всего 2 измерения), это разные фигуры. А с нашей трехмерной точки зрения ( 2+1 = 3 измерения) это все одна и та же фигура: квадрат, которую мы видим под разными углами.

И двухмерник тоже может понять, что это трехмерный квадрат, который он видит под разными углами. А вот это — трехмерный куб, который двумерник видит частично искаженным.

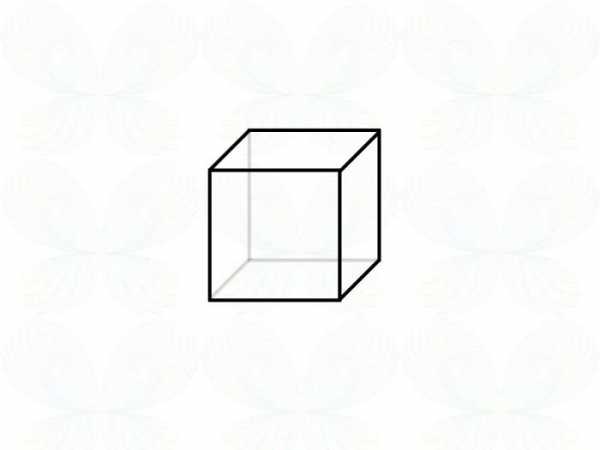
Ну вот и славненько. А если взять наше измерение, то становится понятно, что вот это — четырехмерный гиперкуб. Просто мы его видим частично искаженным.

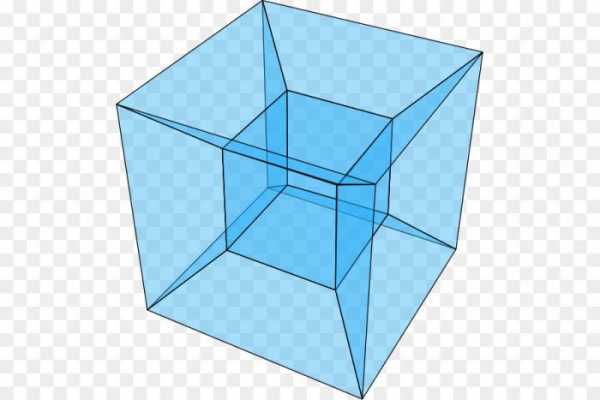
Это восемь кубов, соединенных гранями. Сторонами. И если посмотреть на них с другой проекции, то можно увидеть КАЖДЫЙ куб. Просто нужно вращать тессеракт в 4-м измерении.

По счастью, народ наделал много гифок, в которых именно это и показывает. Что меняя 4-х мерную перспективу, можно видеть ВСЕ кубы. Но в нашем трехмерном мире — только по-очередно.

И квадраты тоже можно видеть все. Ведь куб состоит из квадратов, и тессеракт — тоже.

Вот по-медленнее:

Наш, трехмерный куб — можно развернуть в двумерные квадраты.

И точно так же 4-х мерный тессеракт (он же гиперкуб) можно развернуть в наши 3-мерные кубы.

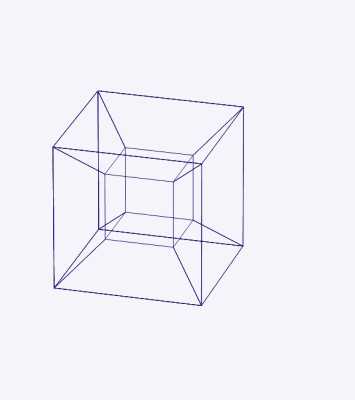
Все )))

Стройте себе тессеракт на 3D принтерах, из спичек, зубочисток и пластилина, паяйте из проволоки, смотрите — и прорывайтесь в четвертое измерение!

Кстати. А существуют ли другие четырехмерные фигуры? Да. Вот это, например, 4-мерная равносторонняя гиперпирамида, если я не ошибаюсь.

Принципе тот же: взяли наши обычные пирамидки, исказили в 4-мерной проекции, соединили гранями.

Трёхмерное пространство — Карта знаний

• Трёхме́рное простра́нство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так как оно имеет три однородных измерения — длину, ширину и высоту, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.

  Понимание трёхмерного пространства людьми, как считается, развивается ещё в младенчестве, и тесно связано с координацией движений человека. Визуальная способность воспринимать окружающий мир органами чувств в трёх измерениях называется восприятием глубины.

  В аналитической геометрии каждая точка трёхмерного пространства описывается как набор из трёх величин — координат. Задаются три взаимно перпендикулярных координатных оси, пересекающихся в начале координат. Положение точки задаётся относительно этих трёх осей заданием упорядоченной тройки чисел. Каждое из этих чисел задаёт расстояние от начала отсчёта до точки, измеренное вдоль соответствующей оси, что равно расстоянию от точки до плоскости, образованной другими двумя осями.

  Также существуют другие системы координат, наиболее часто используются цилиндрическая и сферическая системы.

  Другой взгляд даёт линейная алгебра, где важную роль играет понятие линейной независимости. Пространство трёхмерно по той причине, что высота коробки не зависит от её длины и ширины. На языке линейной алгебры пространство трёхмерно, потому что каждая точка может быть задана комбинацией из трёх линейно независимых векторов. В этих терминах пространство-время четырёхмерно, потому что положение точки во времени не зависит от её положения в пространстве.

  Трёхмерное пространство имеет несколько свойств, которые отличают его от пространств другой размерности. Например, это пространство наименьшей размерности, в котором можно завязать узел на куске верёвки. Многие законы физики, например многие законы обратных квадратов связаны с тем что размерность нашего пространства три.

  Нульмерное, одномерное и двухмерное пространства могут рассматриваться как располагающиеся в трёхмерном пространстве; само оно может считаться частью модели четырёхмерного пространства (четвёртым измерением иногда называют время).

Источник: Википедия

Связанные понятия

В релятивистской физике координатами Риндлера называется важная и полезная координатная система, представляющая часть плоского пространства-времени, также называемого пространством Минковского. Координаты Риндлера были введены Вольфгангом Риндлером для описания пространства-времени равномерно ускоренного наблюдателя.

Подробнее: Координаты Риндлера

Реше́ние Ке́рра — Нью́мена — точное решение уравнений Эйнштейна, описывающее невозмущённую электрически заряженную вращающуюся чёрную дыру без космологического члена. Астрофизическая значимость решения неясна, так как предполагается, что встречающиеся в природе коллапсары не могут быть существенно электрически заряжены. Три вектора (или большее число) называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.

Подробнее: Компланарность

Интервал в теории относительности — аналог расстояния между двумя событиями в пространстве-времени, являющийся обобщением евклидового расстояния между двумя точками. Интервал лоренц-инвариантен, то есть не меняется при переходе от одной инерциальной системы отсчёта к другой, и, даже более, является инвариантом (скаляром) в специальной и общей теории относительности.

Упоминания в литературе

Четыре координаты какого-либо события можно рассматривать как координаты, определяющие положение этого события в четырехмерном пространстве, которое называется пространством-временем. Четырехмерное пространство представить себе невозможно. Лично я с трудом представляю себе даже трехмерное пространство! Но нетрудно изображать графически двумерные пространства, например поверхность Земли. (Поверхность Земли двумерна, потому что положение любой точки можно задать двумя координатами – широтой и долготой.) На диаграммах, которыми я буду, как правило, пользоваться, ось времени направлена вверх, а одна из пространственных осей горизонтальна. Два других пространственных измерения либо будут отсутствовать, либо же одно из них я буду иногда изображать в перспективе. (Такие диаграммы, как диаграмма рис. 2.1, называются пространственно-временными.) Например, на рис. 2.2 ось времени направлена вверх и отсчет на ней ведется в годах, а расстояние от Солнца до звезды альфа Центавра отложено по горизонтальной оси и измеряется в милях. Траектории Солнца и альфы Центавра, возникающие при их перемещении в пространстве-времени, показаны на диаграмме вертикальными линиями: первая – слева, а вторая – справа. Луч света от Солнца распространяется по диагонали, и он доходит от Солнца до альфы Центавра за четыре года. Самоподобие – это ключевое свойство, характеризующее фракталы. Когда вы смотрите на фрактал, то видите набор элементов, который всегда остается одним и тем же. Большинство объектов утрачивает при приближении некоторые свои признаки (такие как симметрия, подобие), фракталы – никогда. Дробная размерность сближает их. Что же такое самоподобие: закон природы или математические конструкции? В качестве рабочего определения можно взять следующее: система называется самоподобной, если из конечного набора ее копий можно собрать, как из детского конструктора, такую же систему, которая больше начальной в определенное количество раз. При упаковке шаров наиболее плотные известные конфигурации обладают решетчатой структурой; для упаковки дисков на плоскости – это гексагональная решетка, в трехмерном пространстве задача еще не решена, предполагается, что это будет кубическая решетка. Для многих веществ, обладающих самоподобием, оптимальная конфигурация атомов – кристаллическая или квазикристаллическая. Для живого оптимальной является их смесь, но со смещением… Аллотропная форма протеина – основа живого – упакована как рецимат этих конфигураций. Из этих и других примеров становится ясно, что при соревновательных механизмах формирования оптимальной конфигурации самоподобие может играть определяющую роль. В известном смысле мы достаточно часто сталкиваемся с постоянной положительной кривизной, правда, с кривизной поверхности, а не пространства. Любые шары есть поверхности постоянной положительной кривизны. Тем не менее, нам трудно вообразить себе сферическое пространство. Мир Евклида, трехмерное пространство нулевой кривизны, входит в нас при рождении. Для простоты мы часто рисуем графы в двух измерениях, но лучше представлять их заполняющими трехмерное пространство, потому что именно его они иллюстрируют. Но здесь есть концептуальная ловушка: линии и узлы графа не занимают конкретные положения в пространстве. Каждый граф определяется только тем, как его части соединяются между собой и как они соотносятся с четко заданными границами (например, с границей области B). Однако нет никакого непрерывного трехмерного пространства, в котором, как может показаться, размещаются графы. Линии и узлы – это и есть пространство, геометрия которого определяется тем, как они соединяются. Трехмерные координаты задаются аналогично двумерным, но к двум составляющим по осям X и Y добавляется третья величина – по оси Z. В трехмерном пространстве аналогично двумерному моделированию можно использовать абсолютные и относительные координаты, а также цилиндрические и сферические, которые схожи с полярными в двумерном пространстве.

Связанные понятия (продолжение)

Сфера Блоха — способ представления чистых состояний кубита в виде точек на сфере. Пространственно-временная диаграмма, также известная как Диаграмма Минковского, была разработана в 1908 г. Германом Минковским и дает иллюстрацию свойств пространства и времени в специальной теории относительности. Она позволяет без математических уравнений качественно понимать такие явления, как замедление времени и Лоренцево сокращение. Кватернионы предоставляют удобное математическое обозначение положения и вращения объектов в пространстве. В сравнении с углами Эйлера, кватернионы позволяют проще комбинировать вращения, а также избежать проблемы, связанной с невозможностью поворота вокруг оси, независимо от совершённого вращения по другим осям (на иллюстрации). В сравнении с матрицами они обладают большей вычислительной устойчивостью и могут быть более эффективными. Кватернионы нашли своё применение в компьютерной графике, робототехнике... Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует её широкому применению. В евклидовой геометрии пересечение двух прямых может быть пустым множеством, точкой или прямой. Различение этих случаев и поиск точки пересечения используется, например, в компьютерной графике, при планировании движения и для обнаружения столкновений. Трилатерация (от лат. trilaterus — трёхсторонний) — метод определения положения геодезических пунктов путём построения на местности системы смежных треугольников, в которых измеряются длины их сторон. Метризуемое пространство — топологическое пространство, гомеоморфное некоторому метрическому пространству. Иначе говоря, пространство, топология которого порождается некоторой метрикой. Геометрия Лобачевского (или гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных прямых, которая заменяется её отрицанием. Диэдральная группа (группа диэдра) — группа симметрии правильного многоугольника, включающая как вращения, так и осевые симметрии. Диэдральные группы являются простейшими примерами конечных групп и играют важную роль в теории групп, геометрии и химии. Хорошо известно и совершенно тривиально проверяется, что группа, образованная двумя инволюциями с конечным числом элементов в области определения является диэдральной группой. Обобщённые координаты — параметры, описывающие конфигурацию динамической системы относительно некоторой эталонной конфигурации в аналитической механике, а конкретно исследовании динамики твёрдых тел в системе многих тел. Эти параметры должны однозначно определять конфигурацию системы относительно эталонной конфигурации. Обобщённые скорости — производные по времени обобщённых координат системы. Ме́трика Шва́рцшильда — это единственное в силу теоремы Биркхофа сферически симметричное точное решение уравнений Эйнштейна без космологической константы в пустом пространстве. В частности, эта метрика достаточно точно описывает гравитационное поле уединённой невращающейся и незаряженной чёрной дыры и гравитационное поле снаружи от уединённого сферически симметричного массивного тела. Названа в честь Карла Шварцшильда, который первым её обнаружил в 1916 году. Пове́рхность в геометрии и топологии — двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве. С другой стороны, существуют поверхности (например, бутылка Клейна), которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения. В математике термин матрица Картана имеет три значения. Все они названы по имени французского математика Эли Картана. Фактически, матрицы Картана в контексте алгебр Ли впервые исследовал Вильгельм Киллинг, в то время как форма Киллинга принадлежит Картану. Поток — обобщение понятия подмногообразия играющее ключевую роль в геометрической теории меры. Яма с бесконечными стенками, в квантовой механике, представляет собой модель частицы, заключённую в «ящике» определённой формы. В одномерном случае этот ящик представляет собой конечный отрезок. Внутри отрезка потенциал считается нулевым. Во всех остальных точках вещественной прямой потенциал обращается в бесконечность. Математически это обычно отражают в граничных условиях, считая, что волновые функции обращаются в нуль на концах отрезка. Данный потенциал является предельным случаем прямоугольной... Отношение инцидентности — это бинарное отношение между двумя различными типами объектов. Это включает понятия, которые можно выразить такими фразами как «точка лежит на прямой» или «прямая принадлежит плоскости». Наиболее существенное отношение инцидентности — между точкой P и прямой l, которое записывается как P I l. Если P I l, пара (P, l) называется флагом. В разговорном языке существует много выражений, описывающих отношение инцидентности (например, прямая проходит через точку, точка лежит на...

Подробнее: Инцидентность (геометрия)

Простая поверхность — поверхность, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям). Более точно, простой поверхностью называется образ гомеоморфного отображения (то есть взаимно однозначного и взаимно непрерывного отображения) внутренности единичного квадрата. Этому определению можно дать аналитическое выражение. Конечная геометрия — это любая геометрическая система, имеющая конечное количество точек. Например, евклидова геометрия не является конечной, так как евклидова прямая содержит неограниченное число точек, а точнее говоря, содержит ровно столько точек, сколько существует вещественных чисел. Конечная геометрия может иметь любое конечное число измерений. В математике особой точкой векторного поля называется точка, в которой векторное поле равно нулю. Особая точка векторного поля является положением равновесия или точкой покоя динамической системы, определяемой данным векторным полем: фазовая траектория с началом в особой точке состоит в точности из этой особой точки, а соответствующая ей интегральная кривая представляет собой прямую, параллельную оси времени.

Подробнее: Особая точка (дифференциальные уравнения)

Координаты Борна в специальной теории относительности — система координат, применяемая для описания вращающейся окружности или (в более общем смысле) диска. Мирова́я ли́ния в теории относительности — кривая в пространстве-времени, описывающая движение тела (рассматриваемого как материальная точка), геометрическое место всех событий существования тела. Иногда мировой линией называют вообще любую непрерывную линию в пространстве-времени. Центра́льное многообра́зие особой точки автономного обыкновенного дифференциального уравнения — инвариантное многообразие в фазовом пространстве, проходящее через особую точку и касающееся инвариантного центрального подпространства линеаризации дифференциального уравнения. Важный объект изучения теории дифференциальных уравнений и динамических систем. В некотором смысле, вся нетривиальная динамика системы в окрестности особой точки сосредоточена на центральном многообразии. Точка округления (круговая точка, омбилическая точка или омбилика) ― точка на гладкой регулярной поверхности в евклидовом пространстве, в которой нормальные кривизны по всем направлениям равны. Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Ориента́ция, в классическом случае — выбор одного класса систем координат, связанных между собой «положительно» в некотором определённом смысле. В математике монодро́ми́ей называется явление, состоящее в преобразовании некоторого объекта при обнесении его вдоль нетривиального замкнутого пути.

Подробнее: Монодромия

Псевдотопологи́ческое простра́нство — множество с дополнительной предельной структурой определённого типа (так называемой псевдотопологией). Исторически понятие псевдотопологического пространства появилось как обобщение топологического пространства. Псевдотопологические пространства были введены в 1959 г. Фишером . Псевдотопологические пространства естественным образом возникают при построении дифференциального исчисления в пространствах без нормы. Топологические пространства можно рассматривать... В теоретической физике диаграмма Пенроуза (названная в честь математического физика Роджера Пенроуза) представляет собой двумерную диаграмму, фиксирующую причинное отношение между различными точками в пространстве-времени. Это расширение диаграммы Минковского, где вертикальное измерение представляет время, горизонтальное — пространство, а наклонные линии под углом 45° соответствуют лучам света. Главное отличие состоит в том, что локально метрика на диаграмме Пенроуза конформно эквивалентна к фактической... Проективная пло́скость — двумерное проективное пространство. Важным частным случаем является вещественная проективная плоскость. Если дано топологическое пространство и группа действий на нём, образы отдельной точки под действием группы действий образуют орбиты действий. Фундаментальная область — это подмножество пространства, которое содержит в точности по одной точке из каждой орбиты. Она даёт геометрическую реализацию абстрактного множества представителей орбит.

Подробнее: Фундаментальная область

В математике путь в топологическом пространстве X — это непрерывное отображение f из единичного отрезка I = в X... Плоскость Фано — конечная проективная плоскость порядка 2, имеющая наименьшее возможное число точек и прямых (7 точек и 7 прямых), с тремя точками на каждой прямой и с тремя прямыми, проходящими через каждую точку. Названа по имени итальянского математика Джино Фано. Индекс особой точки векторного поля — математическое понятие, относящееся к дифференциальной топологии, дифференциальной геометрии, теории динамических систем и теории дифференциальных уравнений. Является топологической характеристикой изолированной особой точки векторного поля и определяется как степень гауссова отображения в данной точке. В классической механике, задача двух тел состоит в том, чтобы определить движение двух точечных частиц, которые взаимодействуют только друг с другом. Распространённые примеры включают спутник, обращающийся вокруг планеты, планета, обращающаяся вокруг звезды, две звезды, обращающиеся вокруг друг друга (двойная звезда), и классический электрон, движущийся вокруг атомного ядра. Пучок — структура, используемая для установления отношений между локальными и глобальными данными. Ве́ктор (от лат. vector, «несущий») — в простейшем случае математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой в евклидовом пространстве (или на плоскости). Задача Вебера обобщает поиск геометрической медианы, для которой цены перевозок полагаются равными для всех точек потребления, и задачу нахождения точки Ферма, геометрической медианы трёх точек. По этой причине задачу иногда называют задачей Ферма – Вебера, хотя то же самое имя используется и для задачи нахождения невзвешенной геометрической медианы. Задача Вебера, в свою очередь, обобщается задачей притяжения – отталкивания, которая позволяет отрицательные цены, так что для некоторых точек большее...

Упоминания в литературе (продолжение)

Трехмерные координаты задаются аналогично двумерным, но к двум составляющим по осям Хи Yдобавляется третья величина – по оси Z. В трехмерном пространстве аналогично двумерному моделированию можно использовать абсолютные и относительные координаты, а также цилиндрические и сферические, которые схожи с полярными в двумерном пространстве. Следовательно, если твердое тело свободно движется в трехмерном пространстве, то оно получает дополнительные три степени свободы, а именно: свободы вращения (поворота) тела относительно каждой из осей координат. А это означает, что всякое твердое тело по сравнению с материальной точкой обладает шестью степенями свободы. Свойство протяженности пространства предполагает, что оно может быть измерено. Соответственно была придумана система измерения протяженности пространства, созданы приборы измерения пространства. В науке и в сознании людей утвердилось представление о том, что материальный мир развивается в трехмерном пространстве. Трёхмерное (пространственное) измерение положено в основу всех объектов человеческой деятельности, в основу изучения всех процессов и явлении реальной действительности. Хотя источники пополнения популяции АСЗ рассмотрены выше достаточно полно, остаются вопросы о том, каков вклад каждого источника в реально наблюдаемую популяцию и насколько сильно характеристики этой популяции искажены наблюдательной селекцией. Эффективным способом ответа на эти вопросы является построение динамической модели устойчивого состояния популяции [Bottke et al., 2002b]. В этой работе численным путем была прослежена эволюция многочисленных виртуальных астероидов, берущих начало в разных источниках: резонансах 3:1 и ν6, диффузных резонансах и в кометах семейства Юпитера. В ходе вычислений регистрировалось время, проведенное каждым астероидом в различных ячейках трехмерной сетки a, e, i за период существования частицы до того или иного финала. Если популяция находится в динамически устойчивом состоянии, то суммарное время, проведенное различными астероидами в отдельных ячейках трехмерного пространства, пропорционально орбитальному распределению тел. Общее распределение АСЗ было найдено как линейная комбинация взвешенного вклада каждого источника. Мир, окружающий нас, является трехмерным, иначе говоря, форму объектов, с которыми человек взаимодействует каждый день, можно описать посредством трех измерений – длины, ширины и высоты. Для создания каждого из этих объектов используются свои способы, о которых люди не задумываются, пока сами не примут участие в создании какого-либо объекта. Точно так же с помощью компьютера и специального программного обеспечения в виртуальном трехмерном пространстве можно создать практически любой объект, вымышленный или встречающийся в повседневной жизни, несколькими способами. Все, что относится к созданию трехмерных объектов и управлению ими в виртуальном пространстве, называется трехмерной графикой. Иначе говоря, трехмерную графику можно определить как виртуальное представление объемной среды. То есть на плоском мониторе компьютера посредством программного обеспечения строится 3D-пространство, которое затем может быть визуализировано с помощью программных средств управления и, в конце концов, в виде неподвижного изображения или анимационного ролика представлено зрителю. Не особыми ли упругими качествами обладает и наше физическое трёхмерное пространство, в лоне которого не утихают процессы нескончаемого его «скручивания» из-за вращений различных небесных тел? Но вот и пластичность завихрённого состояния (наряду с противоположным качеством – упругостью, упорством) сказывается во всём – на Земле, в космосе и в средах особых – психических, социальных. На первый взгляд, это поражает, но, конечно, преисполнено глубочайшего смысла, касается оснований мироздания. Растём ведь в сопротивлении, по принципу – «чем хуже, тем лучше». Яркий и простой пример – длинная, скачущая, танцующая пружина: она подвижна, неуязвима, сберегает свой остов. Сходна так называемая «вихревая нить» в средах физических, и если она замкнута, то образует «вихревое кольцо», тороидальную конструкцию, способную аккумулировать и транслировать энергетические запасы. Природные объекты тоже могут быть моделированы подобной замкнутой скруткой, напоминающей магнитное поле диполя или конвективные потоки, скульптурно, для наглядности представимые универсальной формой яблока (IV гл.). Иногда это тело может выходить из физического и перемещаться как в трехмерном пространстве, так и во времени, являющемся четвертой координатой эфирного дубля. Такой выход происходит во время сна. Иногда в сновидении сознание переходит не в эфирное, а в астральное тело, обладающее пятой пространственной координатой (см. ниже). Начало пути к высшим организмам положило образование клетки. «Маленький кусочек пространства был захвачен, завоеван, включен внутрь себя. Не очень большой шаг в превращении трехмерного пространства из вещи в себе – в вещь для нас. – пишет Р. Л. Берг. – Клетка трехмерна, но микроскопически мала. Топологически клетка двумерна. Математики знают, что это значит. Плоскость – высшее ее достижение, арена всех процессов, протекающих в ней… [выделено мной – Д. М.]»[117].

Размерность пространства — Википедия

Материал из Википедии — свободной энциклопедии

Проекции фигур разной размерности на плоскость

Разме́рность — количество независимых параметров, необходимых для описания состояния объекта, или количество степеней свободы системы.

Существует несколько различных подходов к определению размерности, например

Пространственные измерения[править | править код]

Классические физические теории описывают трёхмерные физические измерения.

• Для того, чтобы описать положение окружности на плоскости, достаточно трёх параметров: двух координат центра и радиуса, то есть: пространство окружностей на плоскости — трёхмерно; пространство точек на той же поверхности — двумерно; тем не менее сама окружность — пространство точек на окружности — одномерна: любая её точка может быть описана одним параметром.
• В рамках ходовых моделей поверхности нашей планеты для определения положения города (город при этом рассматривается не как двумерный объект, а как точка) на поверхности Земли достаточно двух параметров, а именно: географической широты и географической долготы. Соответственно: пространство в таких моделях является двумерным (сокращённо — 2D, от англ. dimension), см. геопространство.
• В рамках ходовых моделей нашей физической реальности для определения положения некоего объекта, к примеру — самолёта (самолёт при этом рассматривается не как трёхмерный объект, а как точка), требуется указать три координаты — дополнительно к широте и долготе нужно знать высоту, на которой он находится. Соответственно: пространство в таких моделях является трёхмерным (3D). К этим трём координатам может быть добавлена четвёртая (время) для описания не только текущего положения самолёта, но и момента времени. Если добавить в модель ориентацию (крен, тангаж, рыскание) самолёта, то добавятся ещё три координаты и соответствующее абстрактное пространство модели станет семимерным.

1. ↑ R. Blei Analysis in integer and fractional dimensions, — New-York: Cambridge university press, — 556 p. — 2003. — ISBN 0-511-01266-7 (netLibrary Edition), ISBN 0-521-65084-4 (hardback).

---

Смотрите также

• 
  Коллектор газовый что это такое
• 
  Кардиолипин что это такое
• 
  Биоскопия что это такое
• 
  Предразрыв сетчатки глаза что это такое
• 
  Неонатолог кто это такой и что он делает
• 
  Хиджама что это такое и от чего помогает
• 
  Мансарда что это такое фото
• 
  Липосаркома что это такое фото
• 
  Априори это что такое
• 
  Сатисфекшн что это такое
• 
  Частное чисел это что такое