Косинус и синус что это такое

Редко используемые тригонометрические функции — Википедия

Материал из Википедии — свободной энциклопедии

Редко используемые тригонометрические функции — функции угла, которые в настоящее время используются редко по сравнению с шестью основными тригонометрическими функциями (синусом, косинусом, тангенсом, котангенсом, секансом и косекансом). К ним относятся:

Определение тригонометрических функций через окружность. Отрезки CD и DE описывают соответственно версинус и эксеканс. Графики версинуса, коверсинуса и гаверсинуса

Синус-верзус (другие написания: версинус, синус версус, называется также «стрелка дуги»). Определяется как versinϑ=1−cos⁡ϑ=2sin2⁡ϑ2.{\displaystyle \operatorname {versin} \,\vartheta =1-\cos \vartheta =2\sin ^{2}{\frac {\vartheta }{2}}.} Представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Иногда используются обозначения versϑ,sinversϑ.{\displaystyle \operatorname {vers} \,\vartheta ,\quad \sin \,\operatorname {vers} \,\vartheta .}

Косинус-верзус (другие написания: коверсинус, косинус версус). Определяется как vercosϑ=versin(π2−ϑ)=1−sin⁡ϑ.{\displaystyle \operatorname {vercos} \,\vartheta =\operatorname {versin} \,\left({\frac {\pi }{2}}-\vartheta \right)=1-\sin \vartheta .} Иногда используются обозначения cvsϑ,cosversϑ.{\displaystyle \operatorname {cvs} \,\vartheta ,\quad \cos \,\operatorname {vers} \,\vartheta .}
Гаверсинус (лат. haversinus, сокращение от half the versed sine). Определяется как haversinϑ=versinϑ2=sin2⁡ϑ2.{\displaystyle \operatorname {haversin} \,\vartheta ={\frac {\operatorname {versin} \,\vartheta }{2}}=\sin ^{2}{\frac {\vartheta }{2}}.} Используется также обозначение havϑ.{\displaystyle \operatorname {hav} \,\vartheta .}
Гаверкосинус (лат. havercosinus, сокращение от half the versed cosine). Определяется как havercosϑ=vercosϑ2=cos2⁡ϑ2.{\displaystyle \operatorname {havercos} \,\vartheta ={\frac {\operatorname {vercos} \,\vartheta }{2}}=\cos ^{2}{\frac {\vartheta }{2}}.} Используется также обозначение hacϑ.{\displaystyle \operatorname {hac} \,\vartheta .}
Эксеканс (лат. exsecant) или экссеканс. Определяется как exsecϑ=sec⁡ϑ−1.{\displaystyle \operatorname {exsec} \,\vartheta =\sec \vartheta -1.}
Экскосеканс — дополнительная функция к эксекансу: excscϑ=exsec(π2−ϑ)=cosecϑ−1.{\displaystyle \operatorname {excsc} \,\vartheta =\operatorname {exsec} \,\left({\frac {\pi }{2}}-\vartheta \right)=\operatorname {cosec} \,\vartheta -1.}

Версинус, коверсинус и гаверсинус были удобны для ручных расчётов с использованием логарифмов, поскольку они всюду неотрицательны, однако в связи с развитием вычислительных средств эта область применения неактуальна. В настоящее время эти функции используются для описания соответствующих сигналов в электронике (например, в функциональных генераторах). Гаверсинус также используется в навигационных расчётах для избежания ошибок округления в вычислительных системах с ограниченной разрядностью.

Тригонометричні функції — Вікіпедія

Матеріал з Вікіпедії — вільної енциклопедії.

Тригонометри́чні фу́нкції — функції кута. Вони можуть бути визначені як відношення двох сторін та кута трикутника або як відношення координат точок кола. Відіграють важливу роль при дослідженні періодичних функцій та багатьох об'єктів. Наприклад, при дослідженні рядів, диференційних рівнянь.

Наведемо шість базових тригонометричних функцій. Останні чотири визначаються через перші дві. Іншими словами, вони є означеннями, а не самостійними сутностями.

синус (sin α)
косинус (cos α)
тангенс (tg α = sin α / cos α)
котангенс (ctg α = cos α / sin α)
секанс (sec α = 1 / cos α)
косеканс (cosec α = 1 / sin α)

Геометричне визначення[ред. | ред. код]

Визначення кутів за допомогою прямокутного трикутника. Визначення тригонометричних функцій на одиничному колі.

Тригонометричні функції можна визначити розглянувши прямокутний трикутник.
Косинусом кута називається відношення довжини прилеглого катета до довжини гіпотенузи:

cos⁡α=ACAB=bc, cos⁡β=BCAB=ac .{\displaystyle \cos \alpha ={\frac {AC}{AB}}={\frac {b}{c}},~~~\cos \beta ={\frac {BC}{AB}}={\frac {a}{c}}~.}

Синусом кута називається відношення довжини протилежного катета до довжини гіпотенузи:

sin⁡α=BCAB=ac, sin⁡β=ACAB=bc .{\displaystyle \sin \alpha ={\frac {BC}{AB}}={\frac {a}{c}},~~~\sin \beta ={\frac {AC}{AB}}={\frac {b}{c}}~.}

Тангенсом кута називається відношення довжини протилежного катета до довжини прилеглого катета:

tg α=BCAC=ab, tg β=ACBC=ba .{\displaystyle {\mbox{tg}}~\alpha ={\frac {BC}{AC}}={\frac {a}{b}},~~~{\mbox{tg}}~\beta ={\frac {AC}{BC}}={\frac {b}{a}}~.}

Котангенсом кута називається відношення довжини прилеглого катета до довжини протилежного катета:

ctg α=ACBC=ba, ctg β=BCAC=ab .{\displaystyle {\mbox{ctg}}~\alpha ={\frac {AC}{BC}}={\frac {b}{a}},~~~{\mbox{ctg}}~\beta ={\frac {BC}{AC}}={\frac {a}{b}}~.}

Аналогічним чином можна визначити тригонометричні функції на колі з одиничним радіусом.

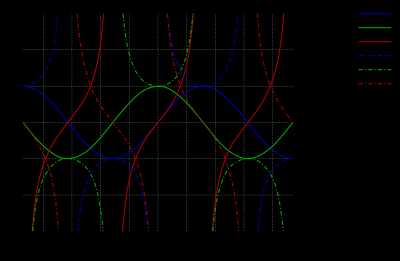
Один період функцій sin(x) та cos(x)

sinx{\displaystyle \sin \,x} та cosx{\displaystyle \cos \,x} це періодичні функції із періодом 2π,{\displaystyle \ 2\pi ,}
tgx{\displaystyle \operatorname {tg} \,x} та ctgx{\displaystyle \operatorname {ctg} \,x} мають період π.{\displaystyle \ \pi .}

Співвідношення, наведені нижче, дозволяють виразити значення тригонометричних функцій від довільного дійсного арґументу через значення функцій для аргументу із інтервалу [0,π2]{\displaystyle [0,{\pi \over 2}]}

sin⁡x=cos⁡(π2−x){\displaystyle \sin x=\cos \left({\pi \over 2}-x\right)}

cos⁡x=sin⁡(π2−x){\displaystyle \cos x=\sin \left({\pi \over 2}-x\right)}

tg⁡x=ctg⁡(π2−x){\displaystyle \operatorname {tg} x=\operatorname {ctg} \left({\pi \over 2}-x\right)}

ctg⁡x=tg⁡(π2−x){\displaystyle \operatorname {ctg} x=\operatorname {tg} \left({\pi \over 2}-x\right)}

Основні співвідношення[ред. | ред. код]

Наступне співвідношення випливає із теореми Піфагора:

sin2⁡x+cos2⁡x=1{\displaystyle ~\sin ^{2}x+\cos ^{2}x=1}

Теореми додавання та формули для кратних кутів[ред. | ред. код]

Формули для функцій суми кутів[ред. | ред. код]

Із основного співвідношення

sin⁡(α+β)=sin⁡αcos⁡β+cos⁡αsin⁡β{\displaystyle \sin {\left(\alpha +\beta \right)}=\sin \alpha \cos \beta +\cos \alpha \sin \beta }

отримуємо

sin⁡(α±β)=sin⁡αcos⁡β±cos⁡αsin⁡β,{\displaystyle \sin {\left(\alpha \pm \beta \right)}=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta ,}

cos⁡(α±β)=cos⁡αcos⁡β∓sin⁡αsin⁡β,{\displaystyle \cos {\left(\alpha \pm \beta \right)}=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta ,}

tg⁡(α±β)=tg⁡α±tg⁡β1∓tg⁡αtg⁡β, ctg⁡(α±β)=ctg⁡αctg⁡β∓1ctg⁡β±ctg⁡α{\displaystyle \operatorname {tg} {\left(\alpha \pm \beta \right)}={{\operatorname {tg} \alpha \pm \operatorname {tg} \beta } \over {1\mp \operatorname {tg} \alpha \operatorname {tg} \beta }},~~~\operatorname {ctg} {\left(\alpha \pm \beta \right)}={{\operatorname {ctg} \alpha \operatorname {ctg} \beta \mp 1} \over {\operatorname {ctg} \beta \pm \operatorname {ctg} \alpha }}}

Формули для функцій подвійних кутів[ред. | ред. код]

sin⁡2α=2sin⁡αcos⁡α{\displaystyle \sin {2\alpha }=2\sin \alpha \cos \alpha }

cos⁡2α=cos2⁡α−sin2⁡α=2cos2⁡α−1=1−2sin2⁡α{\displaystyle \cos {2\alpha }=\cos ^{2}\alpha -\sin ^{2}\alpha =2\cos ^{2}\alpha -1=1-2\sin ^{2}\alpha }

tg⁡2α=2tg⁡α1−tg2⁡α , ctg⁡2α=ctg2⁡α−12ctg⁡α=12(ctg⁡α−tg⁡α){\displaystyle \operatorname {tg} {2\alpha }={{2\operatorname {tg} \alpha } \over {1-\operatorname {tg} ^{2}\alpha }}~,~~~\operatorname {ctg} {2\alpha }={{\operatorname {ctg} ^{2}\alpha -1} \over {2\operatorname {ctg} \alpha }}={1 \over 2}{\left(\operatorname {ctg} \alpha -\operatorname {tg} \alpha \right)}}

Формули для функцій потрійних кутів[ред. | ред. код]

sin⁡3α=3sin⁡α−4sin3⁡α , cos⁡3α=4cos3⁡α−3cos⁡α{\displaystyle \sin {3\alpha }=3\sin \alpha -4\sin ^{3}\alpha ~,~~~\cos {3\alpha }=4\cos ^{3}\alpha -3\cos \alpha }

Формули для функцій половинних кутів[ред. | ред. код]

sin⁡α2=1−cos⁡α2 , cos⁡α2=1+cos⁡α2{\displaystyle \sin {\alpha \over 2}={\sqrt {{1-\cos \alpha } \over 2}}~,~~~\cos {\alpha \over 2}={\sqrt {{1+\cos \alpha } \over 2}}}

tg⁡α2=sin⁡α1+cos⁡α=1−cos⁡αsin⁡α , ctg⁡α2=sin⁡α1−cos⁡α=1+cos⁡αsin⁡α{\displaystyle \operatorname {tg} {\alpha \over 2}={\sin \alpha \over {1+\cos \alpha }}={{1-\cos \alpha } \over \sin \alpha }~,~~~\operatorname {ctg} {\alpha \over 2}={\sin \alpha \over {1-\cos \alpha }}={{1+\cos \alpha } \over \sin \alpha }}

Формули для суми функцій кута[ред. | ред. код]

asin⁡A+bcos⁡B=rsin⁡(A+B)=rcos⁡(π2−A−B), r=a2+b2, tgB=ba{\displaystyle a\sin A+b\cos B=r\sin {\left(A+B\right)}=r\cos \left({\pi \over 2}-A-B\right),~{r={\sqrt {a^{2}+b^{2}}}},~{tgB={b \over a}}}

sin⁡A±sin⁡B=2sin⁡A±B2cos⁡A∓B2{\displaystyle \sin A\pm \sin B=2\sin {{A\pm B} \over 2}\cos {{A\mp B} \over 2}}

cos⁡A+cos⁡B=2cos⁡A+B2cos⁡A−B2{\displaystyle \cos A+\cos B=2\cos {{A+B} \over 2}\cos {{A-B} \over 2}}

cos⁡A−cos⁡B=−2sin⁡A+B2sin⁡A−B2{\displaystyle \cos A-\cos B=-2\sin {{A+B} \over 2}\sin {{A-B} \over 2}}

tg⁡A±tg⁡B=sin⁡A±Bcos⁡Acos⁡B , ctg⁡A±ctg⁡B=sin⁡B±Asin⁡Asin⁡B{\displaystyle \operatorname {tg} A\pm \operatorname {tg} B={\sin {A\pm B} \over {\cos A\cos B}}~,~~\operatorname {ctg} A\pm \operatorname {ctg} B={\sin {B\pm A} \over {\sin A\sin B}}}

Загальні формули для функцій кратних кутів[ред. | ред. код]

Якщо n є цілим додатнім числом, то

sin⁡nA=(n1)cosn−1⁡Asin⁡A−(n3)cosn−3⁡Asin3⁡A+(n5)cosn−5⁡Asin5⁡A∓⋯{\displaystyle \sin {nA}={n \choose 1}\cos ^{n-1}A\sin A-{n \choose 3}\cos ^{n-3}A\sin ^{3}A+{n \choose 5}\cos ^{n-5}A\sin ^{5}A\mp \cdots }

cos⁡nA=cosn⁡A−(n2)cosn−2⁡Asin2⁡A+(n4)cosn−4⁡Asin4⁡A∓⋯{\displaystyle \cos {nA}=\cos ^{n}A-{n \choose 2}\cos ^{n-2}A\sin ^{2}A+{n \choose 4}\cos ^{n-4}A\sin ^{4}A\mp \cdots }

Загальні формули для степенів функцій[ред. | ред. код]

Якщо n є цілим непарним числом, то

sinn⁡x=(−1)n−122n−1[sin⁡nx−(n1)sin⁡(n−2)x+(n2)sin⁡(n−4)x−(n3)sin⁡(n−6)x+⋯+(−1)n−12(nn−12)sin⁡x]{\displaystyle \sin ^{n}x={{(-1)^{{n-1} \over 2}} \over {2^{n-1}}}\left[\sin {nx}-{n \choose 1}\sin {(n-2)x}+{n \choose 2}\sin {(n-4)x}-{n \choose 3}\sin {(n-6)x}+\cdots +(-1)^{{n-1} \over 2}{n \choose {{n-1} \over 2}}\sin x\right]}

cosn⁡x=(12)n−1[cos⁡nx+(n1)cos⁡(n−2)x+(n2)cos⁡(n−4)x+(n3)cos⁡(n−6)x+⋯+(nn−12)cos⁡x]{\displaystyle \cos ^{n}x={\left({1 \over 2}\right)}^{n-1}\left[\cos {nx}+{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}+{n \choose 3}\cos {(n-6)x}+\cdots +{n \choose {{n-1} \over 2}}\cos x\right]}

Якщо n є цілим парним числом, то

sinn⁡x=(−1)n22n−1[cos⁡nx−(n1)cos⁡(n−2)x+(n2)cos⁡(n−4)x−(n3)cos⁡(n−6)x+⋯+(−1)n−22(nn−22)cos⁡2x]+12n(nn2){\displaystyle \sin ^{n}x={{{\left(-1\right)}^{n \over 2}} \over {2^{n-1}}}\left[\cos {nx}-{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}-{n \choose 3}\cos {(n-6)x}+\cdots +{\left(-1\right)}^{{n-2} \over 2}{n \choose {{n-2} \over 2}}\cos {2x}\right]+{1 \over 2^{n}}{n \choose {n \over 2}}}

cosn⁡x=(12)n−1[cos⁡nx+(n1)cos⁡(n−2)x+(n2)cos⁡(n−4)x+(n3)cos⁡(n−6)x+⋯+(nn−22)cos⁡2x]+12n(nn2){\displaystyle \cos ^{n}x={\left({1 \over 2}\right)}^{n-1}\left[\cos {nx}+{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}+{n \choose 3}\cos {(n-6)x}+\cdots +{n \choose {{n-2} \over 2}}\cos {2x}\right]+{1 \over 2^{n}}{n \choose {n \over 2}}}

Розклади в ряд Тейлора[ред. | ред. код]

Існують такі розклади в ряд Тейлора тригонометричних функцій:

sin⁡x=x−x33!+x55!−x77!+⋯=∑n=0∞(−1)nx2n+1(2n+1)!{\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}

cos⁡x=1−x22!+x44!−x66!+⋯=∑n=0∞(−1)nx2n(2n)!{\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}

tg⁡x=∑n=0∞U2n+1x2n+1(2n+1)!=∑n=1∞

Синус — Вікіпедія

Синус (лат. sinus — «пазуха») — тригонометрична функція кута. Визначення синусу гострого кута в контексті прямокутного трикутника: для заданого кута, є відношенням довжини катета, що є протилежним даному куту, до довжини найдовшої сторони трикутника (гіпотенузи).

У загальнішому випадку, визначення синуса (та інших тригонометричних функцій) може бути розширене до значення дійсного числа, що відноситься до довжини певного відрізка в одиничному колі. Більш складні сучасні визначення задають синус як нескінченний ряд або як розв'язок деяких диференційних рівнянь, що дозволяє їх розширення до довільних додатних і від'ємних значень і навіть до комплексних чисел.

Функція синуса зазвичай застосовується в моделюванні періодичних явищ, таких як звукові і світлові хвилі, позиції і швидкості гармонічних коливань, інтенсивності сонячного світла і довжини для, коливань середньої температури в період року.

Функція синус має зв'язок у своєму походженні до функцій джа і коті-джа, що використовувалися в період Гупта в Індійській астрономії (Ар'ябхатія, Сур'я Сіддханта), шляхом перекладу із санскриту на арабську мову, а потім з арабської на латинь^[1]. Слово «синус» походить від неправильного перекладу на латину арабського джиба, яке є транслітерацією слова на санскриті, що означало половину хорди, джа-ардха.^[2]Таблиця синусів містить числові значення функції синусу.

Визначення в контексті прямокутного трикутника[ред. | ред. код]

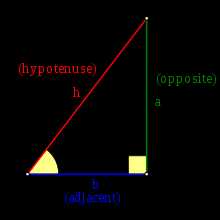Для кута α, функція синусу задає відношення довжини протилежного до кута катету до довжини гіпотенузи, sin⁡α=oppositehypotenuse{\displaystyle \sin \alpha ={\frac {\textrm {opposite}}{\textrm {hypotenuse}}}}

При визначенні тригонометричних функцій для гострого кута α, беруть будь-який прямокутний трикутник який містить кут α; на відповідному малюнку, це геометричний кут A в трикутнику ABC, який має значення α. Три сторони трикутника мають назви:

протилежний катет це сторона протилежна обраному куту, в даному випадку це сторона a.
гіпотенуза це сторона протилежна прямому куту, в даному випадку це сторона h. Гіпотенуза завжди є найдовшою стороною прямокутного трикутника.
прилеглий катет- сторона що залишилась, в даному випадку це сторона b. Це сторона, яка одночасно прилягає до вибраного кута (кут A) і до прямого кута трикутника.

У визначеному трикутнику, синус кута дорівнює довжині протилежного катету поділеному на довжину гіпотенузи (інші тригонометричні функції можуть визначатися аналогічним способом; наприклад, косинус кута є відношенням довжин прилеглого катету до гіпотенузи).

Як уже зазначалося, значення функції sin(α) залежить від вибраного прямокутного трикутника, який містить в собі кут величиною α. Однак, це не є важливим: оскільки всі такі трикутники є подібними, і співвідношення сторін буде однакове в усіх таких трикутниках.

В контексті одиничного кола[ред. | ред. код]

Ілюстрація одиничного кола. Радіус якого дорівнює 1. Змінна t задає значення Кута.

В тригонометрії, одиничне коло це коло з радіусом один і з центром в початку координат (0, 0) декартової системи координат.

Нехай існує довільна пряма через початок координат, яка утворює кут θ із додатною частиною осі x, і перетинає одиничне коло. x- і y-є координатами точки перетину прямої і кола, які дорівнюють cos θ і sin(θ), відповідно. Відстань від точки до початку координат завжди дорівнює 1.

На відміну від визначення в контексті прямокутного трикутника або кута нахилу, використовуючи одиничне коло значення кута можуть бути розширені до повного набору дійсних аргументів. В такому випадку функція синуса є періодичною.

Одиничне коло є в основі принципу побудови координатного транспортиру. При безперервному обертанні кута навколо своєї осі на 360 градусів можна бачити як координата транспортира зміщується по осі Y від -1 до 1. На осі Y в одиничному колі розміщені значення функції синуса.

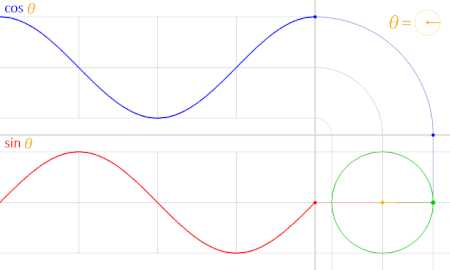Анімація показує як функція синусу (червона) y=sin⁡(θ){\displaystyle y=\sin(\theta )} із значень y-координати (червона точка), що змінюється при окреслені точкою одиничного кола (зелена), і значення кута θ задаються радіанах.

Точні тотожності (застосовуються до радіан): Застосовуються до всіх значень кута θ{\displaystyle \theta }.

sin⁡(θ)=cos⁡(π2−θ)=1csc⁡(θ){\displaystyle \sin(\theta )=\cos \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\csc(\theta )}}}

Обернені[ред. | ред. код]

оберненим числом для синусу є косеканс, тобто обернене число для sin(A) записується як csc(A), або cosec(A). Косеканс задає відношення довжини гіпотенузу до довжини протилежного катету:

csc⁡(A)=1sin⁡(A)=hypotenuseopposite=ha.{\displaystyle \csc(A)={\frac {1}{\sin(A)}}={\frac {\textrm {hypotenuse}}{\textrm {opposite}}}={\frac {h}{a}}.}

Зворотні функції[ред. | ред. код]

Головні значення функції arcsin(x) зображені на декартовій площині. Arcsin є зворотньою функцією від синусу.

Зворотньою функцією для синусу є арксинус (позначається як arcsin або asin) або обернений синус (sin^-1). Оскільки синус не має ін'єктивного відображення, арксинус не є точною зворотньою функцією, а є частковою зворотньою функцією. Наприклад, sin(0) = 0, але також і sin(π) = 0, sin(2π) = 0 і так далі. Звідси випливає, що функція арксинус багатозначна: arcsin(0) = 0, але також і arcsin(0) = π, arcsin(0) = 2π, і т. д.. Коли необхідно мати одне визначене значення, функція може бути обмежена до її головної області значень. Виходячи з цього обмеження, для кожного значення x в усій області значень, вираз arcsin(x) прийматиме лише одне значення, яке називається його головним значенням.

θ=arcsin⁡(oppositehypotenuse)=sin−1⁡(ah).{\displaystyle \theta =\arcsin \left({\frac {\text{opposite}}{\text{hypotenuse}}}\right)=\sin ^{-1}\left({\frac {a}{h}}\right).}

k є деяким цілим значенням:

sin⁡(y)=x ⇔ y=arcsin⁡x+2πk, or y=π−arcsin⁡(x)+2πk{\displaystyle {\begin{aligned}\sin(y)=x\ \Leftrightarrow \ &y=\arcsin x+2\pi k,{\text{ or }}\\&y=\pi -\arcsin(x)+2\pi k\end{aligned}}}

або у вигляді одного рівняння:

sin⁡(y)=x ⇔ y=(−1)karcsin⁡(x)+πk{\displaystyle \sin(y)=x\ \Leftrightarrow \ y=(-1)^{k}\arcsin(x)+\pi k}

Arcsin задовольняє рівнянням:

sin⁡(arcsin⁡(x))=x{\displaystyle \sin(\arcsin(x))=x\!}

arcsin⁡(sin⁡(θ))=θfor −π2≤θ≤π2.{\displaystyle \arcsin(\sin(\theta ))=\theta \quad {\text{for }}-{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}}.}

Обчислення[ред. | ред. код]

Для функції синус:

f(x)=sin⁡(x){\displaystyle f(x)=\sin(x)\,}

Похідною є:

f′(x)=cos⁡(x){\displaystyle f'(x)=\cos(x)\,}

Первісною функції є:

∫f(x)dx=−cos⁡x+C{\displaystyle \int f(x)\,dx=-\cos x+C}

C позначає Сталу інтегрування.

Зв'язок із іншими тригонометричними функціями[ред. | ред. код]

Функції синусу і косинусу можуть бути зв'язані між собою різними виразами. Ці дві функції відрізняються фазою в 90°: sin⁡(π/2−x){\displaystyle \sin(\pi /2-x)} = cos⁡(x){\displaystyle \cos(x)} для всіх кутів x. А також, похідною функції sin(x) є cos(x).

Будь-яку тригонометричну функцію можна виразити через інші тригонометричні функції (з урахуванням знаків плюс та мінус у різних чвертях або за допомогою знакової функції (sgn)).

Через інші тригонометричні функції синус можна виразити наступним чином:

Всі рівняння, в яких використовуються знаки плюс/мінус (±), мають додатні значення для кутів в першій чверті.

Основний зв'язок між синусом і косинусом може виражатися у вигляді Тригонометричної тотожності Піфагора:

cos2⁡(θ)+sin2⁡(θ)=1{\displaystyle \cos ^{2}(\theta )+\sin ^{2}(\theta )=1\!}

де sin²x означає (sin(x))².

Властивості пов'язані із чвертями[ред. | ред. код]

Чотири чверті Декартової системи координат.

В рамках чотирьох чвертей функція синусу має наступні властивості.

Точки на межах чвертей. k є цілим числом.

Для аргументів, яких нема в цій таблиці, значення задані із урахуванням, що функція синусу є періодичною із періодом 360° (або 2π радіан): sin⁡(α+360∘)=sin⁡(α){\displaystyle \sin(\alpha +360^{\circ })=\sin(\alpha )}, або sin⁡(α+180∘)=−sin⁡(α){\displaystyle \sin(\alpha +180^{\circ })=-\sin(\alpha )}. А також cos⁡(x

Теорема синусов — Википедия

Достаточно доказать, что

asin⁡α=2R.{\displaystyle {\frac {a}{\sin \alpha }}=2R.}

Проведем диаметр |BG|{\displaystyle |BG|} для описанной окружности. По свойству углов, вписанных в окружность, угол GCB{\displaystyle GCB} прямой, а угол CGB{\displaystyle CGB} равен либо α{\displaystyle \alpha }, если точки A{\displaystyle A} и G{\displaystyle G} лежат по одну сторону от прямой BC{\displaystyle BC}, либо π−α{\displaystyle \pi -\alpha } в противном случае. Поскольку sin⁡(π−α)=sin⁡α{\displaystyle \sin(\pi -\alpha )=\sin \alpha }, в обоих случаях получаем

a=2Rsin⁡α{\displaystyle a=2R\sin \alpha }.

Повторив то же рассуждение для двух других сторон треугольника, получаем:

asin⁡α=bsin⁡β=csin⁡γ=2R.{\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R.}