Главная » Разное » Самый длинный пример в мире по математике

Самый длинный пример в мире по математике


Математики решили самую сложную задачу в мире

Одна из самых сложных математических загадок в мире поддалась математикам Эндрю Сазерленду из США и Эндрю Букеру из Бристольского университета в Британии. Они вычислили три числа, сумма кубов которых будет равна 42. На расчеты понадобился миллион часов машинного времени.

Задача, поставленная еще в 1954 году, выражена следующим уравнением: x³ + y³ + z³ = k. K — каждое из чисел от 1 до 100. Требовалось найти x, y и z.

Греф признался в ненависти к школе и экзаменам

Подробнее

В течение десятков лет математики искали решения для целых чисел от единицы до 100. Ученым удалось найти значения для всех чисел, кроме 33 и 42. Задачу 33 в итоге решили — это сделал британец Эндрю Букер, который написал новый алгоритм вычислений и прогнал решение через мощный компьютер. Решение было найдено за три недели. Оставалось число 42.

Букер решил заручиться поддержкой своего заокеанского коллеги Эндрю Сазерленда, уточнил сайт Science Alert. Для решения задачи ученые решили использовать сеть Charity Engine, которая объединяет более полумиллиона персональных компьютеров по всему миру в глобальную вычислительную сеть.

На решение задачи потребовалось более миллиона часов машинного времени. В итоге планетарный разум выдал три числа. Целиком уравнение выглядит так: (-80538738812075974)³ + 80435758145817515³ + 12602123297335631³ = 42.

70

человек поделились статьей

Задачи современной математики, которые до сих пор не решены

Как и всегда в математике, если проблема не решается «в лоб», к ней подходят с другого конца. Например, в 2013 году было доказано, что количество простых чисел, отличающихся на 70 миллионов, бесконечно. Тогда же, с разницей менее чем в месяц, значение разницы было улучшено до 59 470 640, а затем и вовсе на порядок — до 4 982 086. На данный момент существуют теоретические обоснования бесконечности пар простых чисел с разницей в 12 и 6, однако доказанной является лишь разность в 246. Как и прочие проблемы такого рода, гипотеза о числах-близнецах особенно важна для криптографии.

Гипотеза Римана

Если кратко, то Бернхард Риман предположил, что распределение простых чисел по множеству всех натуральных чисел не подчиняется каким-либо законам. Но их количество на заданном участке числового ряда коррелирует с распределением определенных значений на графике дзета-функции. Она расположена выше и для каждого s дает бесконечное количество слагаемых. Например, когда в качестве s подставляется 2, то в результате получается уже решенная “базельская задача” — ряд обратных квадратов (1 + 1/4 + 1/9 + 1/16 + …).

Одна из “проблем тысячелетия», за решение которой назначен приз в миллион долларов, а также вхождение в пантеон “богов» современной математики. На деле, доказательство этой гипотезы настолько сильно толкнет вперед теорию чисел, что это событие по праву будет называться историческим. Многие вычисления и утверждения в математике строятся на предположении о том, что “гипотеза Римана» верна, и до сих пор никого не подводили. Немецкий математик сформулировал знаменитую задачу 160 лет назад, и с тех пор к ее решению подступались неисчислимое количество раз, однако прогресс очень скромен.

7 самых сложных логических задач, которые решит только один человек из десяти

7 самых сложных логических задач, которые решит только один человек из десяти

В связи с началом учебного года мы решили проверить, насколько наши подписчики умны и изобретательны. А ты сможешь решить все, представленные нами, задачи?

«ПОСЧИТАЙ-КА»

Давай проверим, умеешь ли ты считать?

Реши без помощи калькулятора вот этот пример: К 1000 нужно прибавить 40, потом еще 1000. Затем приплюсуйте 30. Есть? Теперь снова 1000. Добавьте 20. Еще раз 1000. И напоследок 10.

Сколько получилось?

А теперь проверь все еще раз с помощью своего телефона. Совпало?

«ЧТО БОДРИТ УТРОМ?»

А теперь задачка на логику.

Женщина уронила в стакан, полный кофе, свой перстень. Как он мог остаться сухим?

Как ты думаешь, в чем тут секрет?

«СПИЧКИ ДЕТЯМ НЕ ИГРУШКА»

Сколько спичек на картинке?

«ЗЕЛЕНЫЙ ЧЕЛОВЕЧЕК»

Это та загадка, которую ты решишь с помощью детской наивностью. Мы уверены, её можно отгадать с первого раза! Ответь на вопрос: что нужно сделать, когда видишь зеленого человечка?

Учитель рисует на листке бумаги несколько кружков и спрашивает одного ученика: «Сколько здесь кружков?». «Семь» — отвечает ученик. «Правильно. Так сколько здесь кружков?» — опять спрашивает учитель другого ученика. «Пять» — отвечает тот. «Правильно» — снова говорит учитель. Так сколько же кружков он нарисовал на листке?

Думаешь все так легко? А теперь попробуй решить задачи, которые считаются самыми сложными в мире!

«СУПЕР СУДОКУ»

Первое, над чем мы предлагаем тебе поломать голову – это самая сложная судоку в мире.

Судоку – это японская головоломка с числами. Принцип ее совсем не замысловат. Но ту, которую предложили тебе мы, сможет решить точно не каждый!

«БОГИ ЛОГИЧЕСКИХ ЗАДАЧ»

Есть три бога, A, B, и C, один из которых бог истины, другой бог лжи и третий бог случая, причём неясно, кто из них кто. Бог истины всегда говорит правду, бог лжи обманывает, а бог случая может сказать и то, и другое в произвольном порядке. Необходимо определить, кем является каждый из богов, задав три вопроса, на которые можно ответить «да» или «нет», при этом каждый вопрос задаётся только одному богу. Боги понимают вопросы, но отвечают на своём языке, в котором есть слова «da» и «ja», но неизвестно, какое слово обозначает «да», а какое «нет».

Эта логическая задача за авторством американского философа и логика Джорджа Булоса была впервые опубликована в итальянской газете «la Repubblica» в 1992-м году. Так же в загадке есть комментарии создателей:

– Можно задавать одному богу более чем один вопрос (поэтому другим богам может быть не задано ни одного вопроса вообще).

– Каков будет следующий вопрос и кому он будет задан, может зависеть от ответа на предыдущий вопрос.

– Бог случая отвечает случайным образом, зависящим от подбрасываний монетки, спрятанной в его голове: если выпадет аверс, то отвечает правдиво, если реверс — то врёт.

– Бог случая отвечает «da» или «ja» на любой вопрос, на который можно ответить «да» либо «нет».

Ответы на все задачи можно посмотреть по ссылке.

Found a typo in the text? Select it and press ctrl + enter

Более сложные примеры уравнений | Математика

52. Более сложные примеры уравнений.
Пример 1.

5/(x – 1) – 3/(x + 1) = 15/(x2 – 1)

Общий знаменатель есть x2 – 1, так как x2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x2 – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

или

5x + 5 – 3x + 3 = 15

или

2x = 7 и x = 3½

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x2 – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

Пример 2.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

или

2x2 + 6x – 2x – 6 = 2x2 + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x2. Однако, мы можем от обеих частей уравнения вычесть по 2x2 — от этого уравнение не нарушится; тогда члены с x2 уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

3x = 3 или x = 1

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

что невозможно.

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

6x + 10 = 2x + 18

или

4x = 8 и x = 2

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x2 + 4x – 10 = 2x2 + 16x – 18.

Здесь уже члены с x2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

4x2 – 12x = –8

или

x2 – 3x = –2

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 22 – 3 · 2 = –2 и 2) 12 – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Пример 3.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x2 – 5x + 6 = x2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x2 – x – 2 = x2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x2 – 2x – 3 = x2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Отсюда получим:

–x = –13 и x = 13.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

или

3x + 3 – 2x + 6 = x – 2

или

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

0 = –11,

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Интернет: Интернет и СМИ: Lenta.ru

Мать ученика школы попросила совета у пользователей интернета в решении упражнения по математике, опубликовав просьбу в группе в соцсети Facebook. В результате задача оказалась не по силам современным взрослым многие не смогли понять, что от них требуется.

Тереза Хоппер (Teresa Hopper) опубликовала фотографию примера из учебника по математике для второго класса, в котором учится ее сын. Она пояснила, что сомневается в правильности своего ответа и в целом не до конца уверена, что правильно поняла упражнение.

По условиям задачи, у девочки по имени Карла было три фишки по 100 единиц, 17 фишек по 10 единиц и 16 фишек по единице. Ученику предлагалось ответить на два вопроса: может ли Карла составить два одинаковых трехзначных числа из имеющихся фишек и может ли она сделать это, использовав все фишки, без остатка.

Задача вызвала недоумение у пользователей сети. В комментариях они заметили, что упражнение гораздо сложнее тех задач, что они решали во втором классе. Один из юзеров написал, что имеет степень по математике, однако тоже не до конца понимает, чего от него требуют авторы учебника.

Тем не менее, мать и сын в итоге смогли решить задачу. Они поняли, что в первом ответе нужно сложить по одинаковому числу фишек из каждой категории. Например, 172 — одну за 100, семь за 10 и 2 за единицу. Во втором же вопросе речь шла о том, чтобы сложить все фишки и поделить их на два. Таким образом, правильным ответом будет 243.

Ранее учитель математики Дмитрий Давидюк опубликовал в TikTok лайфхак, помогающий легко складывать дроби с разными знаменателями, под названием «метод бабочки». В комментариях некоторые пользователи сети признали этот способ гениальным.

Не только почитать, но и посмотреть — у нас в Instagram

Пять удивительных математических фактов / Хабр

Для начала небольшой спойлер

Да я знаю, что если написать фамилию с заглавной буквы, казуса не получится. Дальше перевод.

Математика – одна из немногих областей знаний, которая может быть объективно названа истинной, потому что ее теоремы основаны на чистой логике. Но в то же время эти теоремы часто оказываются очень странными и противоречащими интуиции.

Некоторые люди считают математику скучной. Следующие примеры показывают, что она какая угодно, но не такая

5. Случайные наборы данных


Как это ни странно, случайные данные на самом деле не такие уж и случайные. В приведенных данных, представляющих собой все от биржевых курсов до населения городов, высот зданий и протяженностей рек, около 30 процентов всех чисел начинаются с единицы. Меньшее количество начинается с 2, еще меньше с 3 и так далее, с 9 начинается только каждое двадцатое число. И чем больше набор данных, чем шире порядок охватываемых величин, тем сильнее проявляется эта закономерность.
4. Спирали простых чисел


В силу того, что простые числа неделимы (кроме как на единицу и самого себя), и того, что все остальные числа могут быть представлены в виде их произведения, простые числа часто рассматриваются как «атомы» в мире математики. Несмотря на свою важность, распределение простых чисел до сих пор остается тайной. Нет такого правила, которое бы однозначно говорило, какие числа будут простыми и через сколько встретится следующее простое число.

Кажущаяся случайность простых чисел делает факты, обнаруженные в «Скатерти Улама» очень странными.

В 1963 году математик Станислав Улам, обнаружил удивительную закономерность, когда разрисовывал свою записную книжку во время презентации: если записывать целые числа по спирали, простые числа выстраиваются вдоль диагональных линий. Само по себе это не очень удивительно, если помнить, что все простые числа, кроме двойки, нечетные, а диагональные линии в спиралях целых чисел поочередно являются нечетными. Более необычной была тенденция простых чисел лежать преимущественно на одних диагоналях и практически отсутствовать на других. Причем закономерность наблюдалась вне зависимости от того, с какого числа начиналась спираль (с единицы или любого другого).

Даже если масштабировать спираль, чтобы она вмещала гораздо большее количество чисел, можно увидеть, что скопление простых чисел на одних диагоналях гораздо плотнее, чем на других. Существуют математические предположения, объясняющие эту закономерность, но пока они не доказаны.

3. Выворачивание сферы

В одной важной области математики, которая называется топология, два объекта считаются эквивалентными или гомеоморфными, если один из них может быть преобразован в другой путем скручивания или растягивания поверхности. Объекты считаются разными, если для преобразования требуются разрезы или изломы поверхности.

В качестве примера рассмотрим тор – объект в форме пончика. Если поставить его вертикально, расширить одну сторону и вдавить верхушку этой же стороны, то получится цилиндрический объект с ручкой. В среде математиков существует классическая шутка, что топологи не могут отличить пончика от чашки с кофе.

С другой стороны, ленты Мебиуса – петли с единственным перегибом не являются гомеоморфными петлями без перегибов (цилиндры), потому что нельзя распрямить ленту Мебиуса, без того чтобы разрезать ее, перевернуть одну сторону и склеить заново.

Топологов давно интересует вопрос, будет ли сфера гомеоморфной самой себе, будучи вывернутой наизнанку? Другими словами, можно ли выворачивать сферу? На первый взгляд это кажется невозможным, потому что нельзя проткнуть дырку в сфере. Но, оказывается, выворачивание сферы возможно. Как это делается, показано на видео .
Поражает тот факт, что тополог Бернард Морин, который является главным разработчиком приведенного метода выворачивания сферы, слеп.

2. Математика стен


Несмотря на то, что стены могут быть украшены бесконечным количеством завитушек, говоря математическим языком, существует конечное число отдельных геометрических шаблонов. Все периодические рисунки Эшера, обои, плиточные дизайны и вообще все двумерные повторяющиеся группы фигур, могут быть отнесены к той или иной так называемой «плоской кристаллографической группе». И знаете, сколько существует таких групп? Ровно 17.
1. Сонет


«Как сонет Шекспира схватывает саму суть любви, или картина показывает внутреннюю красоту человека, уравнение Эйлера проникает в самые глубины существования.»

Математик из Стэнфорда Кейт Девлин (Keith Devlin) написал эти слова об уравнении в эссе 2002 года, которое называлось «Самое прекрасное уравнение». Но почему от формулы Эйлера перехватывает дыхание? И что она вообще значит?

Во-первых, буква «e» представляет собой иррациональное число (с бесконечным количеством цифр), которое начинается с 2.71828… Открытое в контексте непрерывно начисляемого сложного процента, оно описывает темпы экспоненциального роста от колоний популяций насекомых до радиоактивного распада. В математике число обладает рядом неожиданных свойств, например, оно равняется сумме обратных факториалов от нуля до бесконечности. В конечном счете константа e оккупировала математику, взявшись вроде бы ниоткуда, но оказавшись в большом числе важных уравнений.

Далее. i представляет собой так называемую мнимую единицу – квадратный корень из минус 1. «Так называемую», потому что в реальности не существует числа, которое, будучи умноженным само на себя, в результате дало отрицательное число (потому отрицательные числа не имеют действительных квадратных корней). Но в математике существует большое количество ситуаций, когда приходится извлекать квадратный корень из отрицательного числа. Число i используется как своеобразная пометка того места, где такая операция была произведена.

Пи – отношение длины окружности к ее диаметру, одна из любимых и наиболее интересных констант в математике. Подобно e, она появилась в большом количестве математических и физических формул как будто из ниоткуда.

Константа e, возведенная в степень мнимая единица, умноженная на Пи равняется минус одному. Из уравнения Эйлера следует, что добавление к этому единицы дает ноль. Трудно поверить, что все эти странные числа, одно из которых даже не относится к реальному миру, могут быть так просто скомбинированы. Но это доказанный факт.

Математических примеров

Добро пожаловать на сайт MathExample.com

Этот образовательный ресурс предназначен для приобретения вами практических навыков математики , а также для развития математических способностей у вас и ваших детей.

«Число . - катализатор, который может помочь превратить буйных безумцев в вежливых людей»

~ Филип Дж. Дэвис

Целей сайта:

  • Повышение знаний по математике
  • получение практического опыта решения математических задач
  • Повышение скорости и качества логико-математического мышления
  • Развитие памяти, внимательности и концентрации

Используя этот ресурс вы можете:

  • получить базовые знания о сложении, вычитании, умножении и делении
  • выучить таблицу умножения с практическими упражнениями
  • научиться работать с целыми, десятичными и дробными числами
  • освоить методы решения уравнений
  • практическое правописание

На сайте представлены следующие возможности:

  • создание задач любой сложности
  • печатные листы любого размера
  • решение и исправление результатов онлайн
  • встроенная проверка и отображение ответов по ссылке или QR-коду
  • два режима на компьютере и на мобильном устройстве

Способность мыслить рационально нужно развивать и закреплять, с нами это легче делать!

10+

Создайте рабочие листы математических примеров для деления методом столбца .Номера примера - целых . Ответы всегда положительных и целых . Всего 1 вариант и 5 уровней сложности.

Делитель

Создает примеры с делением целых чисел методом столбца

1 вариант 5 уровней

Вариант: 1 Уровень: Легкий

9+

Создает рабочие листы со словами на английском языке , которые содержат пропущенные буквы.Это должно быть заполнено правильными буквами. Всего 3 варианта и 5 уровней сложности.

Английский словарь

Создает рабочие листы с словарного запаса английского языка , которые содержат пропущенные буквы, которые должны быть заполнены правильными буквами

3 варианта 5 уровней

z & nbsp ro th & nbsp y qui & nbsp
t & nbsp день

3 renault и nbsp Вариант: 3 Уровень: Легкий

6+

Пошаговое сложение задачи на каждый день.Развивает умение решать примеры с операцией сложение .

Дополнение № 19

Попыток: 2 Уровень: Обычный

  • Ответы: 9 ~ 18
  • Примеры: 21
  • Сложение 9

Старт

  • Ответы: 9 ~ 18
  • Примеры: 20
  • Сложение 9

Начало

11+

Создайте рабочие листы математических примеров с сложением и вычитанием .Номера примера - дроби . Ответы всегда положительных . Всего 3 варианта и 3 уровня сложности.

Числитель

Создает примеры с сложением и вычитанием дробей, ответы всегда положительные

3 варианта 3 уровня

Вариант: 1 Уровень: Легкий

14+

Создание рабочих листов с системами уравнений .Номера уравнения - целых . Переменные всегда положительные . Всего 3 варианта и 3 уровня сложности.

Создает систему уравнений , ответы всегда целые числа и положительные

3 варианта 3 уровня

28y ÷ 7x = 10
2y × 11x = 880

Вариант: 2 Уровень: Легкий

Посетителей MathExample.com

Если у вас есть какие-либо вопросы или пожелания по улучшению этого сайта, свяжитесь с нами.
Если на сайте возникают ошибки, также пишите нашим разработчикам.

Поделитесь ссылкой

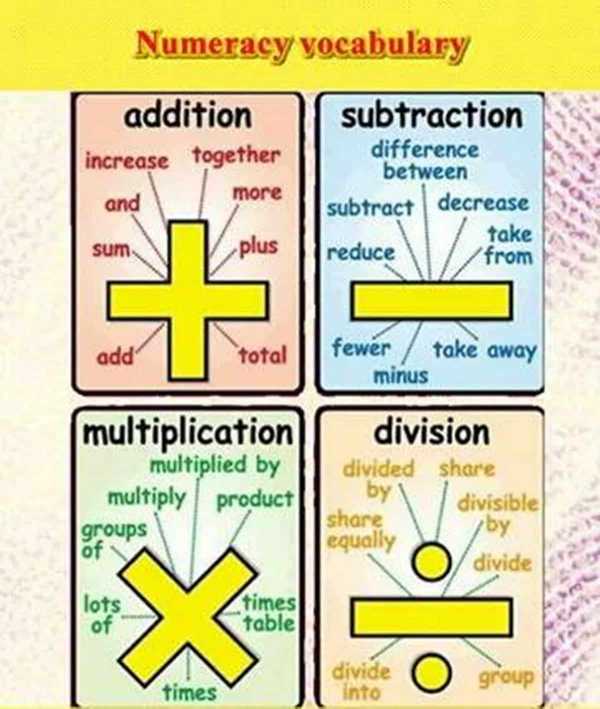
Если у вас есть возможность, сообщите о нас своим друзьям и знакомым, мы будем вам очень благодарны.
.

«Математический словарь» - язык математики

Изучите математический словарь на английском языке с помощью изображений и видео.

Язык математики - это система, используемая математиками для обмена математическими идеями между собой. Этот язык состоит из субстрата некоторого естественного языка (например, английского), использующего технические термины и грамматические соглашения, характерные для математического дискурса, дополненные узкоспециализированной символической нотацией для математических формул.

Математический словарь | Видео

Математический словарь | Картинки

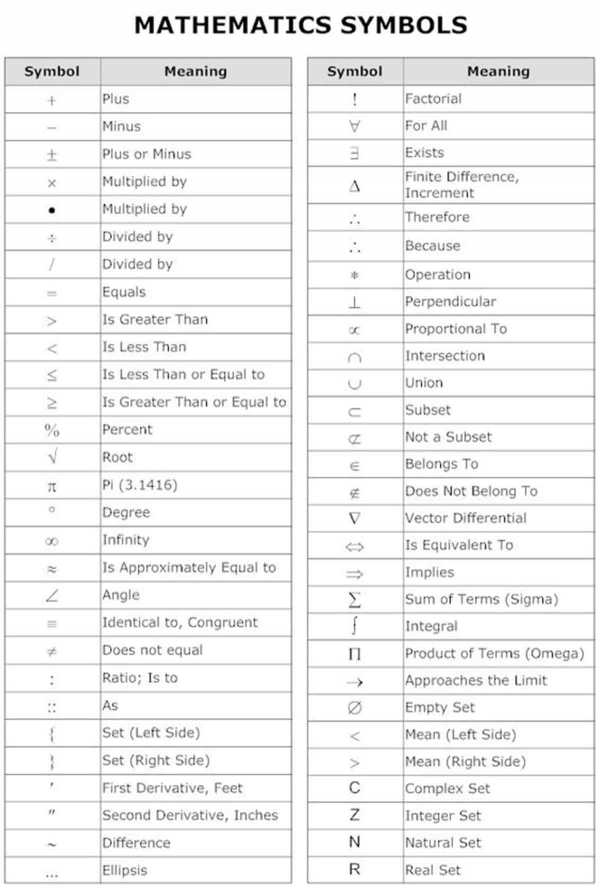Как произносить и писать числа на английском языке

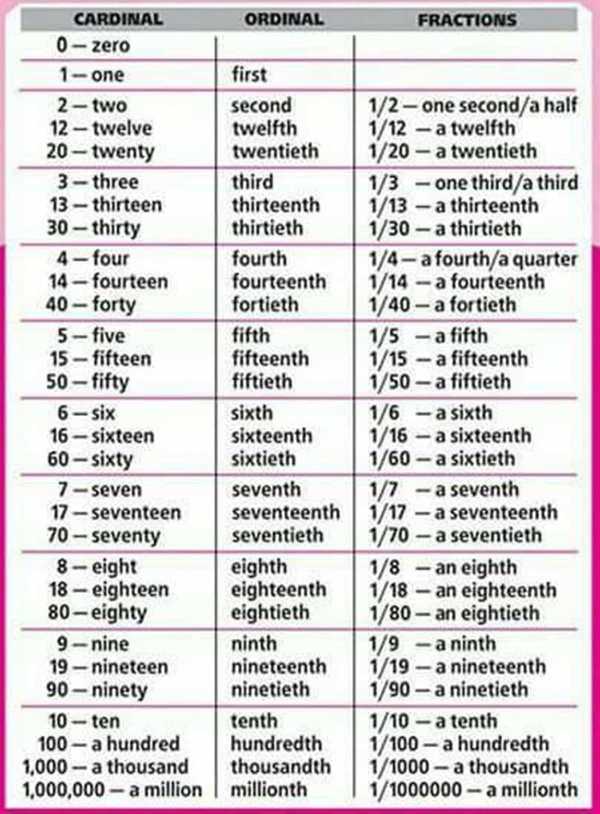Словарь «Углы»

  • Угол, равный 1/4 оборота (90 ° или π / 2 радиана), называется прямым углом .Две прямые, образующие прямой угол, называются нормальными, ортогональными или перпендикулярными.
  • Пара углов, противоположных друг другу, образованная двумя пересекающимися прямыми линиями, образующими X-образную форму, называются вертикальными углами или противоположными углами или вертикально противоположными углами.
  • Углы, превышающие прямой угол и меньшие, чем прямой угол (от 90 ° до 180 °), называются тупыми углами («тупой» означает «тупой»).
  • Угол, равный 1/2 оборота (180 ° или π радиан), называется прямым углом .
  • Углы, превышающие прямой угол, но менее 1 поворота (от 180 ° до 360 °), называются углами отражения.
  • Угол, равный 1 обороту (360 ° или 2π радиан), называется полным углом , полным углом, или перигоном.
  • Углы, которые не являются прямыми или кратными прямым, называются косыми углами.
  • …

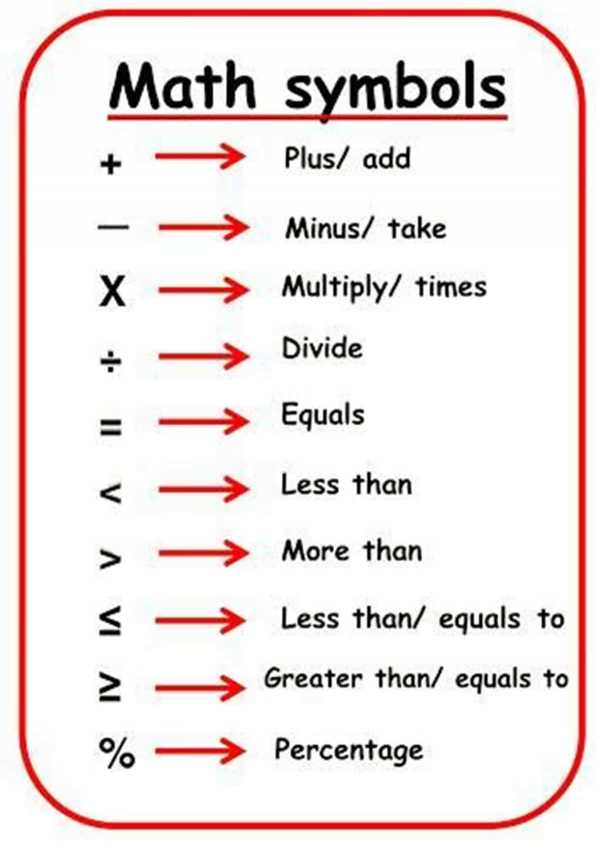
4,7 3 голоса

Рейтинг статьи

.

Математические символы и операции - английский словарь

Это урок английского языка. Это не урок математики! На этом уроке вы выучите английский словарь для основных математических символов и операций:

«математика» - существительное.

Значение :
Изучение чисел, форм и пространства с помощью символов и правил.
Пример : 2 + 2 = 4

Слово «математика» часто сокращается до:

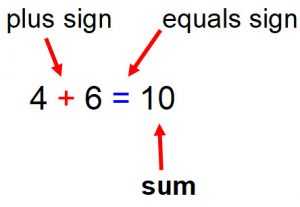
  • «математика» (американский английский)
  • «математика» (британский английский)

Дополнение

« Сложение »

Значение :
Процесс сложения чисел для вычисления суммы.
Пример : Сегодня мы попрактикуемся в сложении.

Чтобы описать сложение выше, мы говорим:
Четыре плюс шесть равно десяти.
или
сумма из четырех и шести равна десяти.

добавить

«добавить» - это глагол.

Значение : сложить два или более чисел для вычисления суммы.
Форма : прибавьте число к числу
Пример : Если вы прибавите четыре к шести, вы получите десять.

Вычитание

«вычитание» - существительное.

Значение : процесс удаления номера из другого номера.
Пример : Давайте научимся вычитанию.

Чтобы описать вычисление вычитания выше, мы говорим:
восемь минус три равно пяти.

вычесть

«вычитать» - это глагол.

Значение : удалить число из другого числа.
Форма : вычтите число из числа
Пример : Если вы вычтете три из восьми, вы получите пять.

забрать

«забрать» - глагол, который также используется для вычитания. Это более неформально, чем «вычитать». Это очень распространено.

Форма : уберите число из числа
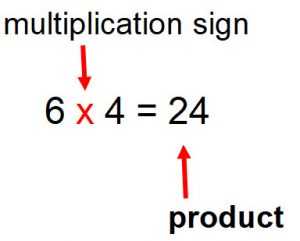
Пример : Уберите три из восьми. Какой ответ?

умножение

существительное «умножение».

Значение : процесс умножения числа.
Пример : Я не очень хорошо умею умножать.


Чтобы описать умножение выше, мы говорим:
Шесть, умноженная на четыре, равняется двадцати четырем.
или
Шесть раз по четыре равно двадцать четыре.

«продукт» существительное.

Значение : результат вычисления умножения.
Пример : Произведение шести на четыре равно двадцать четыре.

умножить

«умножить» - это глагол для умножения.

Форма : умножьте число на число
Пример : Если вы умножите шесть на четыре, вы получите двадцать четыре.

деление

«деление» - существительное.

Пример : Сегодня мы изучим деление.


Чтобы описать вычисление деления выше, мы говорим:

пятнадцать делить на три равно пяти.

делить

«делить» - это глагол.

Форма : разделите число на число
Пример : Если вы разделите пятнадцать на три, вы получите пять.

Больше уроков английского

Уроки английского на нашем канале Youtube
Английские выражения с глаголом KEEP
Модальный глагол ДОЛЖЕН - форма, использование и значение
Сравнение вещей с «как»
Прилагательные в превосходной степени
Список всех уроков

Видеоурок английского

.

Как рассчитать режим или модальное значение

Режим - это просто номер, который чаще всего встречается .

Пример:

В {6, 3, 9, 6, 6, 5, 9, 3} Mode равен 6, как это происходит чаще всего.

В поисках режима

Чтобы найти mode, или модальное значение, лучше всего расположить числа в порядке . Затем посчитайте , сколько каждого числа. Число, которое встречается чаще всего - это режим .

Пример:

3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29

Для заказа это номера:

3, 5, 7, 12, 13, 14, 20, 23, 23, 23, 23 , 29, 39, 40, 56

Это позволяет легко увидеть, какие числа встречаются чаще всего .

В данном случае режим 23 .

Другой пример: {19, 8, 29, 35, 19, 28, 15}

Расположите их по порядку: {8, 15, 19, 19, 28, 29, 35}

19 появляется дважды, все остальные появляются только один раз, поэтому 19 - это режим .

Как запомнить? Думаю, "режим самый"

Более одного режима

У нас может быть более одного режима.

Пример: {1, 3, 3, 3, 4, 4, 6, 6, 6, 9}

3 появляется трижды, как и 6.

Итак, есть два режима: на 3 и 6

Наличие двух режимов называется «бимодальным» .

Наличие более двух режимов называется «мультимодальным» .

Группировка

В некоторых случаях (например, когда все значения появляются одинаковое количество раз) режим бесполезен. Но мы можем сгруппировать значений, чтобы увидеть, есть ли в одной группе больше, чем в других.

Пример: {4, 7, 11, 16, 20, 22, 25, 26, 33}

Каждое значение встречается один раз, поэтому попробуем сгруппировать их.

Мы можем попробовать группы из 10:

  • 0-9: 2 значения (4 и 7)
  • 10-19: 2 значения (11 и 16)
  • 20-29: 4 значения (20, 22, 25 и 26)
  • 30-39: 1 значение (33)

В группах по 10 «20» появляются чаще всего, поэтому в качестве режима можно выбрать 25 (середина группы 20).

Вы можете использовать разные группы и получить другой ответ.

Группировка также помогает найти типичные значения, когда в реальном мире все портится!

Пример: Как долго заполнять поддон?

Филипп записал, сколько времени занимает заполнение поддона в минутах:

{35, 36, 32, 42, 58, 56, 35, 39, 46, 47, 34, 37}

Это занимает больше времени, когда есть перерыв или обед, поэтому среднее значение не очень полезно.

Но группировка по 5 дает:

  • 30-34: 2
  • 35-39: 5
  • 40-44: 1
  • 45-49: 2
  • 50-54: 0
  • 54-59: 2

"35-39" появляются чаще всего, поэтому мы можем сказать, что обычно занимает около 37 минут , чтобы заполнить поддон.

.

Общие математические символы и терминология

Математические символы и терминология могут сбивать с толку и препятствовать изучению и пониманию основ математики.

Эта страница дополняет наши страницы, посвященные навыкам счета, и предоставляет краткий глоссарий общих математических символов и терминологии с краткими определениями.

Мы что-то упускаем? Дайте нам знать.

Общие математические символы

+ сложение, плюс, положительное

Символ сложения + обычно используется для обозначения того, что два или более числа должны быть сложены вместе, например, 2 + 2.

Символ + также может использоваться для обозначения положительного числа, хотя он встречается реже, например, +2. На нашей странице о положительных и отрицательных числах объясняется, что число без знака считается положительным, поэтому плюс обычно не требуется.

Подробнее см. На нашей странице Дополнение .

- вычитание, минус, минус

Этот символ имеет два основных применения в математике:

  1. - используется, когда нужно вычесть одно или несколько чисел, например, 2 - 2.
  2. Символ - также обычно используется для обозначения отрицательного или отрицательного числа, например, -2.
См. Дополнительную информацию на нашей странице о Вычитание .

× или * или. Умножение

Эти символы имеют то же значение; обычно × используется для обозначения умножения, когда написано от руки или используется на калькуляторе, например, 2 × 2.

Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя * имеет другие, более сложные значения в математике.

Реже умножение также может быть обозначено точкой. или вообще без символа. Например, если вы видите число, написанное вне скобок без оператора (символа или знака), то его следует умножить на содержимое скобок: 2 (3 + 2) совпадает с 2 × (3 + 2).

Подробнее см. Нашу страницу Умножение .

÷ или / Подразделение

Оба эти символа используются для обозначения деления в математике.÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.

/ используется в электронных таблицах и других компьютерных приложениях.

Подробнее см. На нашей странице в Division .

= равно

Символ = равно используется, чтобы показать, что значения по обе стороны от него одинаковы. Чаще всего используется для отображения результата вычисления, например 2 + 2 = 4, или в уравнениях, например 2 + 3 = 10-5.

Вы также можете встретить другие похожие символы, хотя они встречаются реже:

  • ≠ означает не равно. Например, 2 + 2 ≠ 5 - 2. В компьютерных приложениях (например, Excel) символы <> означают не равно.
  • ≡ означает идентично. Это похоже на, но не совсем то же самое, что на равно. Поэтому, если сомневаетесь, придерживайтесь =.
  • ≈ означает примерно равно или почти равно.Две стороны отношения, обозначенные этим символом, будут не достаточно точными для математических манипуляций.

<Меньше и> Больше

Этот символ < означает меньше, например 2 <4 означает, что 2 меньше 4.

Этот символ > означает больше, например, 4> 2.

≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре.В компьютерных приложениях используются <= и> =.

≪ ≫ Эти символы встречаются реже и означают намного меньше или намного больше.

± плюс или минус

Этот символ ± означает «плюс» или «минус». Он используется для обозначения, например, доверительных интервалов вокруг числа.

Ответом считается «плюс-минус» другое число, или, другими словами, в пределах диапазона данного ответа.

Например, 5 ± 2 на практике может быть любым числом от 3 до 7.

∑ Сумма

Символ ∑ означает сумму.

∑ - заглавная греческая буква сигма. Он обычно используется в алгебраических функциях, и вы также можете заметить его в Excel - кнопка Автосумма имеет сигму в качестве значка.

° Степень

Градусы ° используются по-разному.

  • В качестве меры вращения - угол между сторонами фигуры или поворот круга.Круг равен 360 °, а прямой угол - 90 °. См. Наш раздел о Geometry для получения дополнительной информации.
  • Мера температуры. градусов по Цельсию или по Цельсию используются в большинстве стран мира (за исключением США). Вода замерзает при 0 ° C и закипает при 100 ° C. В США используется Фаренгейт. По шкале Фаренгейта вода замерзает при 32 ° F и закипает при 212 ° F. Смотрите нашу страницу: Системы измерения для получения дополнительной информации.

∠ Угол

Символ угла ∠ используется как сокращение в геометрии (изучении форм) для описания угла.

Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Аналогичным образом, ∠BAC может использоваться для описания угла точки A (между точками B и C). Подробнее об углах и других геометрических терминах см. На наших страницах Geometry .

√ Квадратный корень

√ - символ квадратного корня. Квадратный корень - это число, которое при умножении на себя дает исходное число.

Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4.Квадратный корень из 9 равен 3, потому что 3 x 3 = 9.

См. Нашу страницу: Специальные числа и понятия для получения дополнительной информации о квадратных корнях.

n Мощность

Целое число с верхним индексом (любое целое число n ) - это символ, используемый для обозначения степени числа.

Например, 3 2 означает 3 в степени 2, что совпадает с 3 в квадрате (3 x 3).

4 3 означает 4 в степени 3 или 4 в кубе, то есть 4 × 4 × 4.

См. Наши страницы Расчетная площадь и Расчет объема , где приведены примеры использования чисел в квадрате и кубе .

Степени также используются как сокращенный способ записи больших и малых чисел.

Большие числа

10 6 - 1 000 000 (один миллион).

10 9 - 1 000 000 000 (один миллиард).

10 12 - 1 000 000 000 000 (один триллион).6 = 10 6 = 1000000 (один миллион).

. Десятичная точка

. - символ десятичной точки, часто называемый просто «точкой». См. Нашу страницу Decimals для примеров его использования.

, Разделитель тысяч

Запятую можно использовать для разделения больших чисел и облегчения их чтения.

Тысячу можно записать как 1000, так и 1000, а миллион - как 1000000 или 1000000.Запятая разделяет большие числа на блоки по три цифры.

В большинстве англоязычных стран, не имеет математической функции, а просто используется для облегчения чтения чисел.

В некоторых других странах, особенно в Европе, вместо десятичной точки может использоваться запятая, и действительно, десятичная точка может использоваться вместо запятой в качестве визуального разделителя. Это объясняется более подробно на нашей странице Introduction to Numbers .

[], () Скобки, круглые скобки

Скобки () используются для определения порядка вычислений в соответствии с правилом BODMAS.

Части расчета, заключенные в скобки, вычисляются первыми, например

  • 5 + 3 × 2 = 11
  • (5 + 3) × 2 = 16

% В процентах

Символ% означает процент или число из 100.

Узнайте все о процентах на нашей странице: Введение в проценты

π Pi

π или Пи - это греческий символ звука «п».Это часто встречается в математике и является математической константой. Пи - это длина окружности круга, деленная на ее диаметр, и имеет значение 3,141592653. Это иррациональное число, что означает, что его десятичные разряды продолжаются до бесконечности.

∞ Бесконечность

Символ ∞ означает бесконечность - понятие, согласно которому числа существуют вечно.

Каким бы большим у вас ни было число, вы всегда можете выбрать номер побольше, потому что вы всегда можете добавить к нему единицу.

Бесконечность - это не число, а идея чисел, существующая вечно. Вы не можете прибавить единицу к бесконечности, как нельзя прибавить единицу к человеку, к любви или ненависти.

x-bar Среднее значение

x-bar - это среднее из всех возможных значений x.

Этот символ чаще всего встречается в статистике.

Дополнительную информацию см. На нашей странице Средние значения .

! Факториал

! это символ факториала.

н! - произведение (умножение) всех чисел от n до 1 включительно, то есть n × (n − 1) × (n − 2) ×… × 2 × 1.

Например:

5! = 5 × 4 × 3 × 2 × 1 = 120

10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800

∝ Пропорциональный

∝ означает «пропорционально » и используется, чтобы показать что-то, что изменяется по отношению к чему-то другому.

Например, если x = 2y, то x ∝ y.

∴ Следовательно

∴ - это удобная сокращенная форма слова «поэтому», используемая в математике и естественных науках.

∵ Потому что

∵ - удобная сокращенная форма слова «потому что», не путать с «поэтому».

Математическая терминология (A-Z)

Амплитуда

Когда объект или точка движутся циклически, или подвергаются вибрации или колебаниям (например, маятник), амплитуда - это максимальное расстояние, на которое он перемещается от своей центральной точки.См. Введение в геометрию для получения дополнительной информации.

Апофема

Линия, соединяющая центр правильного многоугольника с одной из его сторон. Линия перпендикулярна (под прямым углом) в сторону.

Площадь

Геометрическая площадь определяется как пространство, занимаемое плоской формой или поверхностью объекта. Площадь измеряется в квадратных единицах, например в квадратных метрах ( 2 м). Для получения дополнительной информации см. Нашу страницу о площади , площади поверхности и объеме .

Асимптота

Асимптота - это прямая линия или ось, которая конкретно связана с кривой линией. По мере того как изогнутая линия расширяется (стремится) к бесконечности, она приближается к своей асимптоте (то есть расстояние между кривой и асимптотой стремится к нулю, но никогда не касается ее). Это происходит в геометрии и тригонометрии .

Ось

Опорная линия, вокруг которой нарисован, повернут или измерен объект, точка или линия.В симметричной форме ось обычно представляет собой линию симметрии.

Коэффициент

Коэффициент - это число или величина, умножающая другую величину. Обычно его ставят перед переменной . В выражении 6 x 6 - коэффициент, а x - переменная.

Окружность

Окружность - это длина расстояния по краю круга. Это тип периметра , который уникален для круглых форм.Для получения дополнительной информации см. Нашу страницу изогнутые формы .

Данные

Данные представляют собой набор значений, информации или характеристик, которые часто имеют числовой характер. Они могут быть собраны с помощью научного эксперимента или других средств наблюдения. Это могут быть количественных или качественных переменных. Датум - это одно значение одной переменной. См. Нашу страницу Типы данных для получения дополнительной информации.

Диаметр

Диаметр - это термин, используемый в геометрии для определения прямой линии, которая проходит через центр круга или сферы, касаясь окружности или поверхности с обоих концов.Диаметр в два раза больше радиуса .

Экстраполировать

Экстраполяция - это термин, используемый при анализе данных. Это относится к расширению графика, кривой или диапазона значений в диапазон, для которого не существует данных, с выводом значений неизвестных данных из тенденций в известных данных.

Фактор

Коэффициент - это число, которое мы умножаем на другое число. Фактор делится на другое число целое число раз. У большинства чисел есть четное количество факторов.Квадратное число имеет нечетное количество множителей. Простое число имеет два множителя - себя и 1. Простой множитель - множитель, который является простым числом. Например, простые множители 21 равны 3 и 7 (потому что 3 × 7 = 21, а 3 и 7 - простые числа).

Среднее, медиана и мода

Среднее значение (среднее значение) набора данных вычисляется путем сложения всех чисел в наборе данных и последующего деления на количество значений в наборе.Когда набор данных упорядочен от наименьшего к наибольшему, среднее значение является средним значением. Режим - это число, которое встречается чаще всего.

Операция

Математическая операция - это шаг или этап в вычислении, или математическое «действие». Основные арифметические операции - сложение, вычитание, умножение и деление. Порядок, в котором выполняются операции при вычислении, важен. Порядок операций известен как BODMAS .

Математические операции часто называют «суммами». Строго говоря, «сумма» - это операция сложения. В SYN мы имеем в виду операции и вычисления, но в повседневной речи вы часто можете услышать общий термин «суммы», который неверен.

Периметр

Периметр двумерной фигуры - это непрерывная линия (или длина линии), определяющая контур фигуры. Периметр круглой формы называется ее окружностью .Наша страница на Perimeter объясняет это более подробно.

Пропорции

Пропорция - это относительное отношение. Соотношения сравнивают одну часть с другой частью, а пропорции сравнивают одну часть с целым. Например, «3 из 10 взрослых в Англии имеют избыточный вес». Пропорция относится к фракциям .

Пифагор

Пифагор был греческим философом, которому приписывают ряд важных математических и научных открытий, возможно, наиболее значительное из которых стало известно как Теорема Пифагора .

Это важное правило применяется только к прямоугольным треугольникам. В нем говорится, что «квадрат гипотенузы равен сумме квадратов на двух других сторонах».

Количественный и качественный

Количественные данные - это числовые переменные или значения, которые могут быть выражены численно, то есть сколько, сколько, как часто, и получаются путем подсчета или измерения.

Качественные данные - это переменные типа, которые не имеют числового значения и могут быть выражены описательно, т.е.е. с использованием имени или символа и получаются путем наблюдения.

Подробнее см. Нашу страницу о типах данных .

Радиан

Радиан - это единица СИ для измерения углов. Один радиан эквивалентен углу, образуемому в центре окружности дугой, равной по длине радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан.

Радиус

Термин радиус используется в контексте окружностей и других изогнутых форм.Это расстояние от центральной точки круга, сферы или дуги до ее внешнего края, поверхности или окружности . Диаметр в два раза больше радиуса. Для получения дополнительной информации см. Нашу страницу изогнутые формы .

Диапазон

В статистике диапазон данного набора данных - это разница между наибольшим и наименьшим значениями.

Коэффициент

Коэффициент - это математический термин, используемый для сравнения размеров одной части с другой.Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7: 5, 1: 8 или 5: 2: 1.

Стандартное отклонение

Стандартное отклонение набора данных измеряет, насколько данные отличаются от среднего значения, то есть это мера вариации или разброса набора значений. Если разброс данных невелик и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные распространяются в более широком диапазоне

Срок

Термин - это отдельное математическое выражение.Это может быть одно число, одна переменная (например, x ) или несколько констант и переменных, умноженных вместе (например, 3 x 2). Термины обычно разделяются операциями сложения или вычитания. Термин может включать операции сложения или вычитания, но только в скобках, например 3 (2 -x3).

Переменная

Переменная - это коэффициент в математическом выражении, арифметическом соотношении или научном эксперименте, который может изменяться.В эксперименте обычно используются три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x , 6 - это коэффициент , и x - переменная.

Разница

Дисперсия - это статистическое измерение, которое указывает разброс между элементами в наборе данных. Он измеряет, насколько далеко каждый член в наборе от среднего и, следовательно, от каждого другого члена в наборе.

Вектор

Векторы описывают математические величины, которые имеют как величину, так и направление.Векторы встречаются во многих математических и физических приложениях, например изучение движения, где скорость, ускорение, сила, перемещение и импульс являются векторными величинами.

Объем

Объем - это трехмерное пространство, занимаемое твердой или полой формой. Он измеряется кубическими размерами пространства, ограниченного его поверхностями. Объем измеряется в кубических единицах, например м 3 .

.

Как найти уравнения касательных и нормальных прямых

Краткий обзор