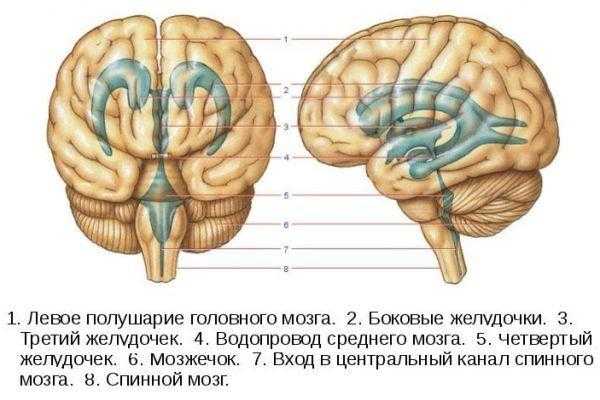
Натуральный ряд чисел что это такое
Натуральные числа. Ряд натуральных чисел. Математика 5 класс
История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.
Натуральные числа – это числа которые мы используем при счете предметов.
Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….
Нуль не относится к натуральным числам.
Все натуральные числа или назовем множество натуральных чисел обозначается символом N.
Таблица натуральных чисел.

Натуральный ряд.
Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.
Свойства натурального ряда:
- Наименьшее натуральное число – единица.
- У натурального ряда следующее число больше предыдущего на единицу. (1, 2, 3, …) Три точки или троеточие ставятся в том случае, если закончить последовательность чисел невозможно.
- Натуральный ряд не имеет наибольшего числа, он бесконечен.
Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5
Пример №2:
Нуль является натуральным числом?
Ответ: нет.
Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.
Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.
Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.
Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.
Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.
Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.
Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.
Ненатуральные числа. Как отличить натуральные от ненатуральных :: SYL.ru
Что же такое натуральные и ненатуральные числа? Как объяснить ребенку, а может и не ребенку, в чем же отличия между ними? Давайте разбираться. Насколько известно, ненатуральные и натуральны числа изучают в 5 классе, и нашей целью является объяснить ученикам так, чтобы они действительно поняли и усвоили, что и как.
История
Натуральные числа - это одно из давних понятий. Давным-давно, когда люди еще не умели считать и не имели понятия о числах, когда им требовалось что-либо пересчитать, к примеру, рыбу, животных, они выбивали на различных предметах точечки или черточки, как это позже выяснилось археологами. В то время им было очень тяжело жить, но цивилизация развилась сначала до римской системы счисления, а затем до десятичной системы счисления. Сейчас же почти все используют арабские цифры

Все о натуральных числах
Натуральные числа - это простые числа, которыми мы пользуемся в повседневной нашей жизни для подсчета предметов для того, чтобы определить количество и порядок. В настоящее время для записи чисел мы используем десятичную систему счисления. Для того чтобы записать любое число, мы используем десять цифр - от нуля до девяти.
Натуральные числа - это те числа, которые мы используем при счете предметов или указании порядкового номера чего-либо. Пример: 5, 368, 99, 3684.
Числовым рядом называют натуральные числа, которые расположены в порядке возрастания, т.е. от единицы до бесконечности. Такой ряд начинается с наименьшего числа - 1, а наибольшего натурального числа не бывает, так как ряд чисел просто бесконечен.
Вообще, ноль - натуральным числом не считается, так как он означает отсутствие чего-либо, и счет предметов так же отсутствует
Арабская система счисления - это современная система, которой мы пользуемся каждый день. Она является одним из вариантов индийской (десятичной).
Такая система счисления стала современной из-за цифры 0, которую и изобрели арабы. До этого в индийской системе она отсутствовала.

Ненатуральные числа. Что это?
К натуральным числам не относятся отрицательные числа и нецелые. Значит, они и есть - ненатуральные числа
Ниже приведены примеры.
Ненатуральные числа бывают:
- Отрицательные числа, например: -1, -5, -36.. и так далее.
- Рациональные числа, которые выражены десятичными дробями: 4,5, -67, 44,6.
- В виде простой дроби: 1/2, 40 2/7 и т.д.
-
Иррациональные числ, такие, как e = 2,71828, √2 = 1,41421 и тому подобное.
Мы надеемся, что очень помогли вам разобраться с ненатуральными и натуральными числами. Теперь вам станет легче объяснить своему малышу данную тему, и он усвоит ее так же хорошо, как великие математики!
НАТУРАЛЬНЫЙ РЯД - это... Что такое НАТУРАЛЬНЫЙ РЯД?
- НАТУРАЛЬНЫЙ РЯД
НАТУРАЛЬНЫЙ РЯД — неограниченно продолжающийся ряд целых положительных чисел, расположенных в порядке их возрастания: 1, 2, 3, 4,... и дальше.
Большая политехническая энциклопедия. - М.: Мир и образование. Рязанцев В. Д.. 2011.
- НАТУРАЛЬНОЕ ЧИСЛО
- НАСЫЩЕННЫЕ УГЛЕВОДОРОДЫ
Смотреть что такое "НАТУРАЛЬНЫЙ РЯД" в других словарях:
НАТУРАЛЬНЫЙ РЯД — бесконечная последовательность 1, 2, 3, 4, 5,..., состоящая из всех натуральных чисел, расположенных в порядке их возрастания. См. также Число … Большой Энциклопедический словарь
натуральный ряд — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN natural scale … Справочник технического переводчика
натуральный ряд — бесконечная последовательность 1, 2, 3, 4, 5..., состоящая из всех натуральных чисел, расположенных в порядке их возрастания. См. также число. * * * НАТУРАЛЬНЫЙ РЯД НАТУРАЛЬНЫЙ РЯД, бесконечная последовательность 1, 2, 3, 4, 5,..., состоящая из… … Энциклопедический словарь
Натуральный ряд — последовательность 1, 2, 3, 4, 5,..., состоящая из всех целых положительных чисел, расположенных в порядке их возрастания. Уже на первых ступенях развития математических наук была понята бесконечность Н. р. Всякое целое положительное… … Большая советская энциклопедия
НАТУРАЛЬНЫЙ РЯД — непустое множество в к ром определена унарная операция S(т. е. S однозначное отображение Nв N), удовлетворяющая условиям (Пеано аксиомы): 1) для любого аиз N: 2) для любых а и bиз N:если то 3) любое подмножество N, к рое содержит 1 и вместе с… … Математическая энциклопедия
НАТУРАЛЬНЫЙ РЯД — бесконечная последовательность 1, 2, 3, 4, 5..., состоящая из всех натуральных чисел, расположенных в порядке их возрастания. См. также Число … Естествознание. Энциклопедический словарь
Натуральный ряд — в первоначальном понимании это правильная (естественно возрастающая) последовательность (множество) натуральных чисел. Всякое множество, эквивалентное множеству чисел натурального ряда, называется счетным. Например, множество квадратов чисел… … Начала современного естествознания
натуральный ряд — матем. Бесконечная последовательность 1, 2, 3, 4, 5..., состоящая из всех целых положительных чисел, расположенных в порядке их возрастания … Словарь многих выражений
НАТУРАЛЬНЫЙ — (лат. naturalis, от natura природа). Естественный, природный, не деланный. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. НАТУРАЛЬНЫЙ лат. naturalis, от natura, природа. Естественный, природный. Объяснение 25000… … Словарь иностранных слов русского языка
НАТУРАЛЬНЫЙ — НАТУРАЛЬНЫЙ, натуральная, натуральное; натурален, натуральна, натурально (лат. naturalis) (книжн.). 1. только полн. Естественный, соответствующий природе вещей. В натуральную величину. || Нефальсифицированный, естественного происхождения, без… … Толковый словарь Ушакова
Хочу все знать: Натуральные числа и шкалы
ЧТО ЭТО? ЦИФРЫ ИЛИ ЧИСЛА?
Аргументируй свой ответ.
ЧТО ТАКОЕ ЦИФРЫ?
Ци́фры (от ср.-лат. cifra от араб. صفر (ṣifr) «пустой, нуль») — система знаков для записи конкретных значений чисел. Цифры нужны для записи чисел (как буквы для записи слов). Цифр 10, а чисел составить их этих десяти цифр можно бесконечное множество.
ВОПРОС
Можно ли назвать самое большое число? Почему?
ЧТО ТАКОЕ ЧИСЛО?
Число — это основное математическое понятие. Числа записывают с помощью комбинаций цифр. Число используют для:- количественной характеристики;
- сравнения;
- обозначения нумерации объектов.
ВОПРОСЫ-ЗАДАНИЯ
Приведи примеры разных чисел.
Какими числами считают предметы? ПРиведи примеры.
Как вы понимаете слово "натуральный"?
НАТУРАЛЬНЫЕ ЧИСЛА
Есть числа, которые люди используют в повседневной жизни для подсчета предметов, т.е. для вычисления их количества и порядка. Такие числа называют натуральными.
С какого числа начинается счет?
Натуральные числа - это числа, начиная с единицы. Они образуются естественным образом при счёте. Например, 1,2,3,4,5... – первые натуральные числа.
Наименьшее натуральное число - один. Наибольшего натурального числа не существует. При счёте число ноль не используют, поэтому ноль НЕ натуральное число.
Натуральный ряд чисел - это последовательность всех натуральных чисел. Запись натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ...
В натуральном ряду каждое число больше предыдущего на единицу.
Как обозначают множество натуральных чисел?
Множество всех натуральных чисел принято обозначать символом N (от лат. naturalis — естественный).Сколько чисел в натуральном ряду?
Натуральный ряд бесконечен, самого большого натурального числа не существует.В какой системе больше всего считает человек?
В десятичной позиционной. Видимо, десять пальцев на руке сложили такую систему исторически. Но есть и другие системы счисления. Подумай, какая система счисления используется в часах? Когда 12=1? Когда 7=1? Когда 2=1?
Как называются числа по количеству цифр в записи?
Расскажи, какие числа называют однозначными, двузначными, пятизначными, многозначными?
В многозначном числе каждая цифра занимает строго определенную позицию, которую называют разрядом числа.
Разряды многозначных чисел
Разряды чисел отсчитывают с его конца.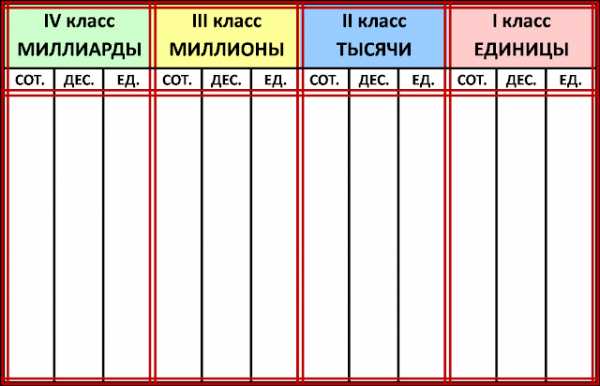
РОЛИК 1
РОЛИК 2
РОЛИК 3
Ряд натуральных чисел
УРОК ДЛЯ ПРОДВИНУТОГО КЛАССА
Натуральный ряд чисел и его свойства.
Изображение натуральных чисел точками на числовой прямой
ТРЕНАЖЕР 1
Соедини названия чисел с записью числа.
натуральный ряд чисел - это... Что такое натуральный ряд чисел?
НАТУРАЛЬНЫЙ РЯД — неограниченно продолжающийся ряд целых положительных чисел, расположенных в порядке их возрастания: 1, 2, 3, 4,... и дальше … Большая политехническая энциклопедия
НАТУРАЛЬНЫЙ РЯД — бесконечная последовательность 1, 2, 3, 4, 5,..., состоящая из всех натуральных чисел, расположенных в порядке их возрастания. См. также Число … Большой Энциклопедический словарь
натуральный ряд — бесконечная последовательность 1, 2, 3, 4, 5..., состоящая из всех натуральных чисел, расположенных в порядке их возрастания. См. также число. * * * НАТУРАЛЬНЫЙ РЯД НАТУРАЛЬНЫЙ РЯД, бесконечная последовательность 1, 2, 3, 4, 5,..., состоящая из… … Энциклопедический словарь
Натуральный ряд — в первоначальном понимании это правильная (естественно возрастающая) последовательность (множество) натуральных чисел. Всякое множество, эквивалентное множеству чисел натурального ряда, называется счетным. Например, множество квадратов чисел… … Начала современного естествознания
Натуральный ряд — последовательность 1, 2, 3, 4, 5,..., состоящая из всех целых положительных чисел, расположенных в порядке их возрастания. Уже на первых ступенях развития математических наук была понята бесконечность Н. р. Всякое целое положительное… … Большая советская энциклопедия
НАТУРАЛЬНЫЙ РЯД — непустое множество в к ром определена унарная операция S(т. е. S однозначное отображение Nв N), удовлетворяющая условиям (Пеано аксиомы): 1) для любого аиз N: 2) для любых а и bиз N:если то 3) любое подмножество N, к рое содержит 1 и вместе с… … Математическая энциклопедия
НАТУРАЛЬНЫЙ РЯД — бесконечная последовательность 1, 2, 3, 4, 5..., состоящая из всех натуральных чисел, расположенных в порядке их возрастания. См. также Число … Естествознание. Энциклопедический словарь
натуральный ряд — матем. Бесконечная последовательность 1, 2, 3, 4, 5..., состоящая из всех целых положительных чисел, расположенных в порядке их возрастания … Словарь многих выражений
НАТУРАЛЬНЫЙ — (лат. naturalis, от natura природа). Естественный, природный, не деланный. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. НАТУРАЛЬНЫЙ лат. naturalis, от natura, природа. Естественный, природный. Объяснение 25000… … Словарь иностранных слов русского языка
НАТУРАЛЬНЫЙ — НАТУРАЛЬНЫЙ, натуральная, натуральное; натурален, натуральна, натурально (лат. naturalis) (книжн.). 1. только полн. Естественный, соответствующий природе вещей. В натуральную величину. || Нефальсифицированный, естественного происхождения, без… … Толковый словарь Ушакова
ряд — натуральный ряд чисел упорядоченный список значений — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы натуральный ряд чиселупорядоченный список… … Справочник технического переводчика
Целое число — Википедия
Целые числа — расширение множества натуральных чисел[1], получаемое добавлением к нему нуля и отрицательных чисел[2]. Необходимость рассмотрения целых чисел продиктована невозможностью в общем случае вычесть из одного натурального числа другое — можно вычитать только меньшее число из большего. Введение нуля и отрицательных чисел делает вычитание такой же полноценной операцией, как сложение[3].
Вещественное число является целым, если его десятичное представление не содержит дробной части (но может содержать знак). Примеры вещественных чисел:
- Числа 142857; 0; −273 являются целыми.
- Числа 5½; 9,75 не являются целыми.
Множество целых чисел обозначается Z{\displaystyle \mathbb {Z} } (от нем. Zahlen — «числа»[4]). Изучением свойств целых чисел занимается раздел математики, называемый теорией чисел.
Положительные и отрицательные числа[править | править код]
Согласно своему построению, множество целых чисел состоит из трёх частей:
- Натуральные числа (или, что то же самое, целые положительные). Они возникают естественным образом при счёте (1, 2, 3, 4, 5…)[5].
- Ноль — число, обозначаемое 0{\displaystyle 0}. Его определяющее свойство: 0+n=n+0=n{\displaystyle 0+n=n+0=n} для любого числа n{\displaystyle n}.
- Целые отрицательные числа.
Отрицательные числа при записи помечаются спереди знаком минус: −1,−2,−3…{\displaystyle -1,-2,-3\dots } Для каждого целого числа a{\displaystyle a} существует и единственно противоположное ему число, обозначаемое −a{\displaystyle -a} и обладающее тем свойством, что a+(−a)=0.{\displaystyle a+(-a)=0.} Если a{\displaystyle a} положительно, то противоположное ему отрицательно, и наоборот. Ноль противоположен самому себе[2].
Абсолютной величиной целого числа a{\displaystyle a} называется это число с отброшенным знаком[6]. Обозначение: |a|.{\displaystyle \left|a\right|.}
- Примеры: |4|=4; |−5|=5; |0|=0{\displaystyle \left|4\right|=4;\ \left|-5\right|=5;\ \left|0\right|=0}
Во множестве целых чисел определены три основные арифметические операции: сложение, обратное к сложению вычитание и умножение. Имеется также важная операция, специфическая для натуральных и целых чисел: деление с остатком. Наконец, для целых чисел определён порядок, позволяющий сравнивать числа друг с другом.
Сложение и вычитание[править | править код]
Следующая таблица иллюстрирует основные свойства сложения[7] для любых целых a,b,c{\displaystyle a,b,c}:
При сложении и вычитании целых чисел выполняются следующие правила знаков[7][8], которые следует учитывать при раскрытии скобок:
- −(−a)=a; −(a+b)=−a−b; −(a−b)=−a+b.{\displaystyle -\left(-a\right)=a;\ -\left(a+b\right)=-a-b;\ -\left(a-b\right)=-a+b.}
Правила сложения целых чисел[9].
- При сложении целых чисел с одинаковыми знаками надо сложить их абсолютные величины и приписать ей знак слагаемых. Пример; −14+(−28)=−42{\displaystyle -14+\left(-28\right)=-42}.
- При сложении целых чисел с разными знаками надо сравнить их абсолютные величины, из большей вычесть меньшую и приписать результату знак того слагаемого, у которого абсолютная величина больше. Примеры: −4+9=9−4=5; −9+4=−(9−4)=−5{\displaystyle -4+9=9-4=5;\ -9+4=-\left(9-4\right)=-5}.
- Вычитание a−b{\displaystyle a-b} для целых чисел всегда выполнимо, и результат можно найти как a+(−b).{\displaystyle a+\left(-b\right).} Пример: 26−51=26+(−51)=−25{\displaystyle 26-51=26+\left(-51\right)=-25}.
- Геометрически сложение можно наглядно представить как смещение числа вдоль числовой оси (см. рисунок в начале статьи), причём прибавление положительного числа вызывает смещение направо, а отрицательного — налево. Например, для числа −3{\displaystyle -3} прибавление к нему 4{\displaystyle 4} означает смещение его вправо на 4 единицы; наглядно видно, что получается +1{\displaystyle +1}. Аналогично −3+(−4){\displaystyle -3+\left(-4\right)}, смещая −3{\displaystyle -3} влево на 4 единицы, получим в результате −7{\displaystyle -7}.
- Вычитание можно наглядно представить аналогично, но в этом случае, наоборот, вычитание положительного числа вызывает смещение влево, а отрицательного — вправо. Например, 5−7{\displaystyle 5-7} смещает 5{\displaystyle 5} на 7 единиц к числу −2{\displaystyle -2}, а 5−(−7){\displaystyle 5-\left(-7\right)} смещает его вправо к числу 12{\displaystyle 12}.
Умножение и возведение в степень[править | править код]
Умножение чисел a,b{\displaystyle a,b} далее обозначается a×b{\displaystyle a\times b} или (только в случае буквенных обозначений) просто ab{\displaystyle ab}. Следующая таблица иллюстрирует основные свойства умножения[7] для любых целых a,b,c{\displaystyle a,b,c}:
При умножении целых чисел выполняются правила знаков[7][8], которые следует учитывать при раскрытии скобок:
- (−a)b=a(−b)=−ab; (−a)(−b)=ab{\displaystyle \left(-a\right)b=a\left(-b\right)=-ab;\ \left(-a\right)\left(-b\right)=ab}
Следствие: произведение чисел с одинаковыми знаками положительно, с разными — отрицательно.
Возведение в натуральную степень целых чисел определяется так же, как и для натуральных чисел:
- an=a⋅a⋅…⋅a⏟n{\displaystyle a^{n}=\underbrace {a\cdot a\cdot \ldots \cdot a} _{n}}
Свойства возведения в степень целых чисел также такие же, как у натуральных:
- (ab)n=anbn;aman=am+n;(am)n=amn{\displaystyle \left(ab\right)^{n}=a^{n}b^{n};\quad a^{m}a^{n}=a^{m+n};\quad \left(a^{m}\right)^{n}=a^{mn}}
В дополнение к этому определению, принято соглашение о нулевой степени: a0=1{\displaystyle a^{0}=1} для любого целого a.{\displaystyle a.} Основанием для такого соглашения служит желание сохранить приведенные выше свойства и для нулевого показателя степени: a0an=a0+n=an,{\displaystyle a^{0}a^{n}=a^{0+n}=a^{n},} откуда ясно, что a0=1.{\displaystyle a^{0}=1.}
Упорядоченность[править | править код]
Z{\displaystyle \mathbb {Z} } — линейно упорядоченное множество. Порядок в нём задаётся соотношениями:
- ⋯−2<−1<0<1<2<…{\displaystyle \dots -2<-1<0<1<2<\dots }
Целое число положительно, если оно больше нуля, отрицательно, если меньше нуля. Положительными целыми числами являются натуральные числа и только они. Отрицательные числа — это числа, противоположные положительным. Ноль не является ни положительным, ни отрицательным. Любое отрицательное число меньше любого положительного[2].
Для любых целых чисел a,b,c,d{\displaystyle a,b,c,d} справедливы следующие соотношения[10].
- Если a<b{\displaystyle a<b}, то для любого c{\displaystyle c} будет a+c<b+c{\displaystyle a+c<b+c}.
- Если a<b{\displaystyle a<b} и c<d{\displaystyle c<d}, то a+c<b+d{\displaystyle a+c<b+d}.
- Если a<b{\displaystyle a<b} и c>0{\displaystyle c>0}, то ac<bc{\displaystyle ac<bc}.
- Если a<b{\displaystyle a<b} и c<0{\displaystyle c<0}, то ac>bc{\displaystyle ac>bc}.
Для сравнения двух отрицательных чисел существует правило: больше то число, у которого абсолютная величина меньше[10]. Например, −6<−5{\displaystyle -6<-5}.
Делимость[править | править код]
Деление с остатком[править | править код]
Операция деления, вообще говоря, не определена на множестве целых чисел. Например, нельзя разделить 3{\displaystyle 3} на 2{\displaystyle 2} — нет такого целого числа, которое, умноженное на 2{\displaystyle 2}, даст 3{\displaystyle 3}. Но можно определить так называемое деление с остатком[11]:
- Для любых целых a,b{\displaystyle a,b} (где b≠0{\displaystyle b\neq 0}) существует единственный набор целых чисел q,r{\displaystyle q,r} такой, что a=bq+r{\displaystyle a=bq+r}, где 0⩽r<|b|.{\displaystyle 0\leqslant r<\left|b\right|.}
Здесь a — делимое, b — делитель, q — (неполное) частное, r — остаток от деления (всегда неотрицателен). Если остаток равен нулю, говорят, что деление выполняется нацело[11].
- Примеры
На операции деления с остатком основаны теория сравнений и алгоритм Евклида.
Деление нацело. Делители[править | править код]
Как определено выше, число a{\displaystyle a} делится (нацело) на число b{\displaystyle b}, если существует целое число q{\displaystyle q} такое, что a=bq{\displaystyle a=bq}. Символическая запись: b|a{\displaystyle b|a}. Существуют несколько равносильных словесных формулировок указанной делимости[12]:
Каждое целое число n{\displaystyle n}, не равное нулю или ±1{\displaystyle \pm 1}, имеет 4 тривиальных делителя: 1,−1,n,−n{\displaystyle 1,-1,n,-n}. Если других делителей нет, число называется простым[13].
Понятие наибольшего общего делителя двух целых чисел, разложение целого числа на простые множители и основная теорема арифметики для целых чисел практически совпадают (с возможным учётом знака) с аналогами этих понятий для натуральных чисел[14].
Существуют практические задачи, в которых необходимо округлить вещественное значение до целого, то есть заменить его на ближайшее (в ту или иную сторону) целое. Поскольку выполнять округление можно разными способами, для уточнения можно использовать «символы Айверсона»[15]:
- ⌊x⌋{\displaystyle \lfloor x\rfloor } — ближайшее к x{\displaystyle x} целое в меньшую сторону (функция «пол», англ. floor, или «целая часть»). Традиционно используются также обозначение Гаусса [x]{\displaystyle [x]} или обозначение Лежандра E(x){\displaystyle E\left(x\right)}.
- ⌈x⌉{\displaystyle \lceil x\rceil } — ближайшее к x{\displaystyle x} целое в бо́льшую сторону (функция «потолок», англ. ceiling).
В зависимости от особенностей постановки задачи, могут встретиться и другие методы: округлить до ближайшего целого или отсечь дробную часть (последний вариант для отрицательных x{\displaystyle x} отличается от функции «целая часть»).
Другой класс задач, связывающих целые и вещественные числа — приближение вещественного числа отношением целых, то есть рациональным числом. Доказано, что любое вещественное число можно с любой желаемой точностью приблизить рациональным, наилучшим инструментом для такого приближения служат непрерывные (цепные) дроби[16].
Развитие математики началось с навыков практического счёта (один, два, три, четыре…), поэтому натуральные числа возникли ещё в доисторический период как идеализация конечного множества однородных, устойчивых и неделимых предметов (людей, овец, дней и т. п.). Сложение появилось как математическая модель таких важных событий, как объединение нескольких множеств (стад, мешков и т. д.) в одно, а вычитание отражало, наоборот, отделение части множества. Умножение для натуральных чисел появилось в качестве, так сказать, пакетного сложения: 3 × 4 означало сумму «3 раза по 4», то есть 4 + 4 + 4. Свойства и взаимосвязь операций открывались постепенно[17][18].
Начальным шагом на пути расширения натуральных чисел стало появление нуля; первыми этот символ стали применять, по-видимому, индийские математики. Вначале ноль применялся не как число, а как цифра при позиционной записи чисел, затем постепенно стал признавать
Ряд обратных простых чисел — Википедия
Сумма обратных величин простых чисел неограниченно растёт. Ось x представлена в логарифмической шкале, что показывает, что расхождение очень медленное. Красная линия является нижней оценкой и тоже растёт неограниченно.Ряд обратных простых чисел расходится. То есть:
- ∑p prime1p=12+13+15+17+111+113+117+⋯=∞{\displaystyle \sum _{p{\text{ prime}}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty }
Этот факт доказал Леонард Эйлер в 1737[1], что усилило результат Евклида (3-й век до нашей эры), что существует бесконечно много простых чисел.
Существует целый ряд доказательств результата Эйлера, включая оценку нижней границы частичных сумм, которая утверждает, что
- ∑p primep≤n1p⩾lnln(n+1)−lnπ26{\displaystyle \sum _{\scriptstyle p{\text{ prime}} \atop \scriptstyle p\leq n}{\frac {1}{p}}\geqslant \ln \ln(n+1)-\ln {\frac {\pi ^{2}}{6}}}
для всех натуральных чисел n. Двойной натуральный логарифм (ln ln) говорит о том, что расхождение ряда очень медленное. См. статью «Константа Майсселя — Мертенса».
Расходимость данного ряда была доказана Эйлером. Для этого он рассматривал гармонический ряд:
∑n=1∞1n=1+12+13+14+⋯=∞{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots =\infty }
А также следующее «тождество», с помощью которого он также показал, что множество простых чисел бесконечно:
∑n=1∞1n=∏p(1+1p+1p2+⋯)=∏p11−p−1{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=\prod _{p}\left(1+{\frac {1}{p}}+{\frac {1}{p^{2}}}+\cdots \right)=\prod _{p}{\frac {1}{1-p^{-1}}}}
Здесь произведение берётся по всем простым числам. Такие бесконечные произведения сегодня называются произведениями Эйлера[en]. Произведение выше является отражением основной теоремы арифметики. Эйлер заметил, что если бы количество простых чисел было конечным, то произведение справа должно было бы сходиться, что противоречит расходимости гармонического ряда.
Доказательство Эйлера[править | править код]
Продолжая рассуждения, описанные выше, Эйлер взял натуральный логарифм от каждой из сторон. Затем он использовал разложение в ряд Тейлора −ln(1−x)=x+x22+x33+x44+…{\textstyle -\ln(1-x)=x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}+{\frac {x^{4}}{4}}+\dots }, а также сходимость обратных степенных рядов:
- ln(∑n=1∞1n)=ln(∏p11−p−1)=−∑pln(1−1p)=∑p(1p+12p2+13p3+⋯)=∑p1p+12∑p1p2+13∑p1p3+14∑p1p4+⋯=A+12B+13C+14D+⋯=A+K{\displaystyle {\begin{aligned}\ln \left(\sum _{n=1}^{\infty }{\frac {1}{n}}\right)&{}=\ln \left(\prod _{p}{\frac {1}{1-p^{-1}}}\right)=-\sum _{p}\ln \left(1-{\frac {1}{p}}\right)\\&{}=\sum _{p}\left({\frac {1}{p}}+{\frac {1}{2p^{2}}}+{\frac {1}{3p^{3}}}+\cdots \right)\\&{}=\sum _{p}{\frac {1}{p}}+{\frac {1}{2}}\sum _{p}{\frac {1}{p^{2}}}+{\frac {1}{3}}\sum _{p}{\frac {1}{p^{3}}}+{\frac {1}{4}}\sum _{p}{\frac {1}{p^{4}}}+\cdots \\&{}=A+{\frac {1}{2}}B+{\frac {1}{3}}C+{\frac {1}{4}}D+\cdots \\&{}=A+K\end{aligned}}}
с фиксированной константой K < 1. Затем он использовал свойство
- ∑n=1∞1n=ln∞,{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=\ln \infty ,}
вывод которого от объяснил, например, в более поздней работе 1748 года[2], путём присвоения x = 1 в разложении Тейлора
- ln(11−x)=∑n=1∞xnn.{\displaystyle \ln \left({\frac {1}{1-x}}\right)=\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}.}
Это позволило ему заключить, что
- A=12+13+15+17+111+⋯=lnln∞.{\displaystyle A={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+\cdots =\ln \ln \infty .}
Предположительно, Эйлер подразумевал, что сумма обратных величин к простым числам, меньших n, асимптотически растёт как ln ln n при стремлении n к бесконечности. Оказалось, что это на самом деле имеет место и более точную версию этого факта строго доказал Франц Мертенс в 1874[3]. Эйлер же получил правильный результат с помощью нестрогих методов.
Доказательство Эрдёша путём оценки сверху и снизу[править | править код]
Следующее доказательство от противного принадлежит Палу Эрдёшу.
Пусть pi означает i-ое простое число. Представим, что сумма обратных величин простым числам сходится. Т.е.
- ∑i=1∞1pi<∞{\displaystyle \sum _{i=1}^{\infty }{\frac {1}{p_{i}}}<\infty }
Тогда существует наименьшее положительное целое число k, такое, что
- ∑i=k+1∞1pi<12(1){\displaystyle \sum _{i=k+1}^{\infty }{\frac {1}{p_{i}}}<{\frac {1}{2}}\qquad (1)}
Для положительного целого x пусть Mx означает множество n из набора {1, 2, …, x}, которые не делятся на любое простое, большее pk (или, эквивалентно, все n⩽x{\displaystyle n\leqslant x}, которые являются произведением степеней простых чисел pi⩽pk{\displaystyle p_{i}\leqslant p_{k}}). Мы можем теперь вывести верхнюю и нижнюю оценку |Mx|{\displaystyle |M_{x}|}, числа элементов в Mx{\displaystyle M_{x}}. Для больших x эти границы приводят к противоречию.
Оценка сверху:
- Любое n в Mx может быть записан в виде n=m2r{\displaystyle n=m^{2}r} c положительными целыми m и r, где r — свободное от квадратов число. Поскольку только k простых p1,…,pk{\displaystyle p_{1},\ldots ,p_{k}} может быть (с показателем 1) в разложении на простые числа r, есть не более 2k различных возможностей для r. Более того, имеется не более x{\displaystyle {\sqrt {x}}} возможных значений для m. Это даёт верхнюю оценку
- |Mx|≤2kx(2){\displaystyle |M_{x}|\leq 2^{k}{\sqrt {x}}\qquad (2)}
Оценка снизу:
- Оставшиеся x−|Mx|{\displaystyle x-|M_{x}|} чисел в разности множеств {1, 2, …, x} \ Mx все делятся на простые числа, большие pk{\displaystyle p_{k}}. Пусть Ni,x{\displaystyle N_{i,x}} означает множество таких n из {1, 2, …, x}, которые делятся на i-ое простое pi{\displaystyle p_{i}}. Тогда
- {1,2,…,x}∖Mx=⋃i=k+1∞Ni,x{\displaystyle \{1,2,\ldots ,x\}\smallsetminus M_{x}=\bigcup _{i=k+1}^{\infty }N_{i,x}}
- Поскольку число целых чисел Ni,x{\displaystyle N_{i,x}} не превосходит xpi{\displaystyle {\tfrac {x}{p_{i}}}} (на самом деле, равно нулю для pi>x{\displaystyle p_{i}>x}), получаем
- x−|Mx|⩽∑i=k+1∞|Ni,x|<∑i=k+1∞xpi{\displaystyle x-|M_{x}|\leqslant \sum _{i=k+1}^{\infty }|N_{i,x}|<\sum _{i=k+1}^{\infty }{\frac {x}{p_{i}}}}
- Используя (1), отсюда получаем
- x2<|Mx|(3){\displaystyle {\frac {x}{2}}<|M_{x}|\qquad (3)}
Получаем противоречие — если x⩾22k+2{\displaystyle x\geqslant 2^{2k+2}}, оценки (2) и (3) не могут выполняться одновременно, поскольку x2⩾2kx{\displaystyle {\tfrac {x}{2}}\geqslant 2^{k}{\sqrt {x}}}.
Доказательство того, что ряд растёт со скоростью log-log[править | править код]
Есть другое доказательство, которое даёт нижнюю оценку частичных сумм. В частности, это показывает, что эти суммы растут по меньшей мере как ln ln n. Доказательство является вариантом идеи разложения произведения Эйлером. Ниже по тексту суммы или произведения по p всегда представляют собой суммы или произведения по определённым множествам простых чисел.
Доказательство опирается на следующие четыре неравенства:
- Любое положительное целое i может быть единственным образом представлено в виде произведения свободных от квадратов чисел и квадрата. Это даёт неравенство
- ∑i=1n1i⩽∏p≤n(1+1p)∑k=1n1k2{\displaystyle \sum _{i=1}^{n}{\frac {1}{i}}\leqslant \prod _{p\leq n}{\left(1+{\frac {1}{p}}\right)}\sum _{k=1}^{n}{\frac {1}{k^{2}}}},
- где для любого i между 1 и n (разложенное) произведение соответствует свободной от квадратов части числа i, а сумма соответствует квадратной части числа i (см. статью «Основная теорема арифметики»).
- ln(n+1)=∫1n+1dxx=∑i=1n∫ii+1dxx⏟<1i<∑i=1n1i{\displaystyle {\begin{aligned}\ln(n+1)&=\int _{1}^{n+1}{\frac {dx}{x}}\\&=\sum _{i=1}^{n}\underbrace {\int _{i}^{i+1}{\frac {dx}{x}}} _{{}\,<\,{\frac {1}{i}}}\\&<\sum _{i=1}^{n}{\frac {1}{i}}\end{aligned}}}
- ∑k=1n1k2<1+∑k=2n(1k−12−1k+12)⏟=1k2−14>1k2=1+23−1n+12<53{\displaystyle {\begin{aligned}\sum _{k=1}^{n}{\frac {1}{k^{2}}}&<1+\sum _{k=2}^{n}\underbrace {\left({\frac {1}{k-{\frac {1}{2}}}}-{\frac {1}{k+{\frac {1}{2}}}}\right)} _{=\,{\frac {1}{k^{2}-{\frac {1}{4}}}}\,>\,{\frac {1}{k^{2}}}}\\&=1+{\frac {2}{3}}-{\frac {1}{n+{\frac {1}{2}}}}<{\frac {5}{3}}\end{aligned}}}
Комбинируя все эти неравенства, мы получаем
- ln(n+1)<∑i=1n1i≤∏p≤n(1+1p)∑k=1n1k2<53∏p≤nexp(1p)=53exp(∑p≤n1p){\displaystyle {\begin{aligned}\ln(n+1)&<\sum _{i=1}^{n}{\frac {1}{i}}\\&\leq \prod _{p\leq n}{\left(1+{\frac {1}{p}}\right)}\sum _{k=1}^{n}{\frac {1}{k^{2}}}\\&<{\frac {5}{3}}\prod _{p\leq n}{\exp \left({\frac {1}{p}}\right)}\\&={\frac {5}{3}}\exp \left(\sum _{p\leq n}{\frac {1}{p}}\right)\end{aligned}}}
После деления на 53{\displaystyle {\tfrac {5}{3}}} и взятия натурального логарифма от обеих частей получим
- lnln(n+1)−ln53<∑p≤n1p{\displaystyle \ln \ln(n+1)-\ln {\frac {5}{3}}<\sum _{p\leq n}{\frac {1}{p}}},
что и требовалось доказать. ∎
Используя
- ∑k=1∞1k2=π26{\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k^{2}}}={\frac {\pi ^{2}}{6}}}
(см. «Базельская задача»), константу выше ln53=0,51082…{\displaystyle \ln {\tfrac {5}{3}}=0{,}51082\ldots } можно улучшить до lnπ26=0,4977…{\displaystyle \ln {\tfrac {\pi ^{2}}{6}}=0{,}4977\ldots }. Фактически, оказывается что
- limn→∞(∑p≤n1p−lnlnn)=M{\displaystyle \lim _{n\to \infty }\left(\sum _{p\leq n}{\frac {1}{p}}-\ln \ln n\right)=M},
где M=0,261497…{\displaystyle M=0{,}261497\ldots } — константа Майсселя — Мертенса (нечто аналогичное более известной постоянной Эйлера — Маскерони).
Доказательство из неравенства Дюзара[править | править код]
Из неравенства Дюзара мы имеем
- pn<nlnn+nlnlnn{\displaystyle p_{n}<n\ln n+n\ln \ln n\quad } для n⩾6{\displaystyle n\geqslant 6}
Тогда
- ∑n=1∞1pn⩾∑n=6∞1pn⩾∑n=6∞1nlnn+nlnlnn⩾∑n=6∞12nlnn=∞{\displaystyle {\begin{aligned}\sum _{n=1}^{\infty }{\frac {1}{p_{n}}}&\geqslant \sum _{n=6}^{\infty }{\frac {1}{p_{n}}}\\&\geqslant \sum _{n=6}^{\infty }{\frac {1}{n\ln n+n\ln \ln n}}\\&\geqslant \sum _{n=6}^{\infty }{\frac {1}{2n\ln n}}=\infty \end{aligned}}}
согласно интегральному признаку сходимости Коши — Маклорена. Это показывает, что ряд слева расходится.
В то время как частичные суммы обратных величин для простых чисел в конечном счёте достигает любое целое значение, они никогда не могут быть равны целому числу.
Одно из доказательств[4] этого делается по индукции — первая частичная сумма равна
Вещественное число — Википедия
Веще́ственное, или действи́тельное, число[1] — математический объект, возникший из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких вычислительных операций, как извлечение корня, вычисление логарифмов, решение алгебраических уравнений, исследование поведения функций[2].
Если натуральные числа возникли в процессе счёта, рациональные — из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое, помимо чисел рациональных, включает элементы, называемые иррациональными числами.
Наглядно понятие вещественного числа можно представить при помощи числовой прямой. Если на прямой выбрать направление, начальную точку и единицу длины для измерения отрезков, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой и, обратно, каждой точке прямой можно поставить в соответствие некоторое вещественное число, притом только одно. Вследствие этого соответствия термин «числовая прямая» обычно употребляется в качестве синонима множества вещественных чисел.
Понятие вещественного числа прошло долгий путь становления. Ещё в Древней Греции в школе Пифагора, которая в основу всего ставила целые числа и их отношения, было открыто существование несоизмеримых величин (несоизмеримость стороны и диагонали квадрата), то есть в современной терминологии — чисел, не являющихся рациональными. Вслед за этим Евдоксом Книдским была предпринята попытка построить общую теорию числа, включавшую несоизмеримые величины. После этого, на протяжении более двух тысяч лет, никто не ощущал необходимости в точном определении понятия вещественного числа, несмотря на постепенное расширение этого понятия[3]. Лишь во второй половине XIX века, когда развитие математического анализа потребовало перестройки его основ на новом, более высоком уровне строгости, в работах К. Вейерштрасса, Р. Дедекинда, Г. Кантора, Э. Гейне, Ш. Мере[3] была создана строгая теория вещественных чисел.
С точки зрения современной математики, множество вещественных чисел — непрерывное упорядоченное поле. Это определение, или эквивалентная система аксиом, в точности определяет понятие вещественного числа в том смысле, что существует только одно, с точностью до изоморфизма, непрерывное упорядоченное поле.
Множество вещественных чисел имеет стандартное обозначение — R («полужирное R»), R{\displaystyle \mathbb {R} } или R{\displaystyle \mathbf {R} }, Unicode U+211D: ℝ) (англ. blackboard bold «R») от лат. realis — действительный.
История становления понятия вещественного числа[править | править код]
Наивная теория вещественных чисел[править | править код]
Первая развитая числовая система, построенная в Древней Греции, включала только натуральные числа и их отношения (пропорции, в современном понимании — рациональные числа). Однако вскоре выяснилось, что для целей геометрии и астрономии этого недостаточно: например, отношение длины диагонали квадрата к длине его стороны не может быть представлено ни натуральным, ни рациональным числом[4].
Для выхода из положения Евдокс Книдский ввёл, в дополнение к числам, более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма. Теория Евдокса дошла до нас в изложении Евклида («Начала», книга V). По существу, теория Евдокса — это геометрическая модель вещественных чисел. С современной точки зрения, число при таком подходе есть отношение двух однородных величин — например, исследуемой и единичного эталона. Следует, однако, подчеркнуть, что Евдокс остался верен прежней традиции — не рассматривал такое отношение как число; из-за этого в «Началах» многие теоремы о свойствах чисел затем заново доказываются для величин. Классическая теория Дедекинда для построения вещественных чисел по своим принципам чрезвычайно похожа на изложение Евдокса. Однако модель Евдокса неполна во многих отношениях, например, не содержит аксиомы непрерывности, не даёт общей теории арифметических операций для величин или их отношений и др.[5]
Ситуация начала меняться в первые века н. э. Уже Диофант Александрийский, вопреки прежним традициям, рассматривает дроби так же, как и натуральные числа, а в IV книге своей «Арифметики» даже пишет об одном результате: «Число оказывается не рациональным»[6]. После гибели античной науки на передний план выдвинулись математики Индии и стран ислама, для которых любой результат измерения или вычисления считался числом. Эти взгляды постепенно взяли верх и в средневековой Европе[7], где поначалу разделяли рациональные и иррациональные (буквально: «неразумные») числа (их называли также мнимыми, абсурдными, глухими и т. п.). Полное уравнение в правах иррациональных чисел связано с трудами Симона Стевина (конец XVI века), который провозгласил[6]:
| Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной законченностью. |
Он же, с некоторыми оговорками, легализовал отрицательные числа, а также развил теорию и символику десятичных дробей, которые с этого момента начинают вытеснять неудобные шестидесятеричные.
Спустя столетие Ньютон в своей «Универсальной арифметике» (1707 года) даёт классическое определение (вещественного) числа как отношения результата измерения к единичному эталону[8]:
| Под числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой-нибудь величины к другой величине того же рода, принятой за единицу. |
Долгое время это прикладное определение считалось достаточным, так что практически важные свойства вещественных чисел и функций не доказывались, а считались интуитивно очевидными (из геометрических или кинематических соображений). Например, считался самоочевидным тот факт, что непрерывная кривая, точки которой расположены по разные стороны от некоторой прямой, пересекает эту прямую. Строгое определение понятия непрерывности также отсутствовало[9]. Как следствие, немало теорем содержали ошибки, нечёткие или чрезмерно широкие формулировки.
Даже после того, как Коши разработал достаточно строгий фундамент анализа, положение не изменилось, поскольку теории вещественных чисел, на которую обязан был опираться анализ, не существовало. Из-за этого Коши сделал немало ошибок, положившись на интуицию там, где она приводила к неверным выводам: например, он полагал, что сумма ряда из непрерывных функций всегда непрерывна.
Создание строгой теории[править | править код]
Первую попытку заполнить пробел в основаниях математики сделал Бернард Больцано в своей статье «Чисто аналитическое доказательство теоремы, что между любыми двумя значениями, дающими результаты противоположного знака, лежит по меньшей мере один действительный корень уравнения» (1817 год). В этой пионерской работе ещё нет целостной системы вещественных чисел, но уже приводится современное определение непрерывности и показывается, что на этой основе теорема, упомянутая в заглавии, может быть строго доказана[10]. В более поздней работе[11] Больцано даёт набросок общей теории вещественных чисел, по идеям близкой к канторовской теории множеств[12], но эта его работа осталась неопубликованной при жизни автора и увидела свет только в 1851 году. Взгляды Больцано значительно опередили своё время и не привлекли внимания математической общественности.
Современная теория вещественных чисел была построена во второй половине XIX века, в первую очередь трудами Вейерштрасса, Дедекинда и Кантора. Они предложили различные, но эквивалентные подходы к теории этой важнейшей математической структуры и окончательно отделили это понятие от геометрии и механики[13].
Конструктивные способы определения вещественного числа[править | править код]
При конструктивном определении понятия вещественного числа, на основе известных математических объектов (например, множества рациональных чисел Q{\displaystyle \mathbb {Q} }), которые принимают заданными, строят новые объекты, которые, в определённом смысле, отражают наше интуитивное понимание о понятии вещественного числа. Существенным отличием между вещественными числами и этими построенными объектами является то, что первые, в отличие от вторых, понимаются нами лишь интуитивно и пока не являются строго определённым математическим понятием.
Эти объекты и объявляют вещественными числами. Для них вводят основные арифметические операции, определяют отношение порядка и доказывают их свойства.
Исторически первыми строгими определениями вещественного числа были именно конструктивные определения. В 1872 году были опубликованы одновременно три работы: теория фундаментальных последовательностей Кантора, теория Вейерштрасса (в современном варианте — теория бесконечных десятичных дробей) и теория сечений в области рациональных чисел Дедекинда[3][14].
Теория фундаментальных последовательностей Кантора[править | править код]
В данном подходе вещественное число рассматривается как предел последовательности рациональных чисел. Чтобы последовательность рациональных чисел сходилась, на неё накладывается условие Коши:
∀ε>0∃N(ε):∀n>N(ε)∀m>0|an+m−an|<ε{\displaystyle \forall \varepsilon >0\;\exists N(\varepsilon ):\;\forall n>N(\varepsilon )\;\forall m>0\;|a_{n+m}-a_{n}|<\varepsilon }Смысл этого условия заключается в том, что члены последовательности, начиная с некоторого номера будут лежать сколь угодно близко друг от друга. Последовательности, удовлетворяющие условию Коши, называются фундаментальными.
Вещественное число, определяемое фундаментальной последовательностью рациональных чисел {an}{\displaystyle \{a_{n}\}}, обозначим [an]{\displaystyle [a_{n}]}.
Два вещественных числа
α=[an]{\displaystyle \alpha =[a_{n}]} и β=[bn]{\displaystyle \beta =[b_{n}]},
определённые соответственно фундаментальными последовательностями {an}{\displaystyle \{a_{n}\}} и {bn}{\displaystyle \{b_{n}\}}, называются равными, если
limn→∞(an−bn)=0{\displaystyle \lim _{n\to \infty }\left(a_{n}-b_{n}\right)=0}Если даны два вещественных числа α=[an]{\displaystyle \alpha =[a_{n}]} и β=[bn]{\displaystyle \beta =[b_{n}]}, то их суммой и произведением называются числа, определённые соответственно суммой и произведением последовательностей {an}{\displaystyle \{a_{n}\}} и {bn}{\displaystyle \{b_{n}\}}:
α+β=def[an+bn]α⋅β=def[an⋅bn]{\displaystyle \alpha +\beta {\overset {\text{def}}{=}}[a_{n}+b_{n}]\qquad \alpha \cdot \beta {\overset {\text{def}}{=}}[a_{n}\cdot b_{n}]}Отношение порядка на множестве вещественных чисел устанавливается посредством соглашения, в соответствии с которым число α=[an]{\displaystyle \alpha =[a_{n}]} по определению больше числа β=[bn]{\displaystyle \beta =[b_{n}]}, то есть α>β{\displaystyle \alpha >\beta }, если
∃ε>0∃N:∀n>Nan⩾bn+ε{\displaystyle \exists \varepsilon >0\;\exists N:\;\forall n>N\;a_{n}\geqslant b_{n}+\varepsilon }Способ построения множества вещественных чисел с помощью фундаментальных последовательностей рациональных чисел является частным случаем конструкции пополнения произвольного метрического пространства. Как и в общем случае, полученное в результате пополнения множество вещественных чисел само уже является полным, то есть содержит пределы всех фундаментальных последовательностей своих элементов.
Теория бесконечных десятичных дробей[править | править код]
Вещественное число определяется как бесконечная десятичная дробь, то есть выражение вида
±a0,a1a2…an…{\displaystyle \pm a_{0},a_{1}a_{2}\ldots a_{n}\ldots }где ±{\displaystyle \pm } есть один из символов +{\displaystyle +} или −{\displaystyle -}, называемый знаком числа, a0{\displaystyle a_{0}} — целое неотрицательное число, a1,a2,…an,…{\displaystyle a_{1},a_{2},\ldots a_{n},\ldots } — последовательность десятичных знаков, то есть элементов числового множества {0,1,…9}{\displaystyle \{0,1,\ldots 9\}}.
Бесконечная десятичная дробь интерпретируется как такое число, которое на числовой прямой лежит между рациональными точками вида
±a0,a1a2…an{\displaystyle \pm a_{0},a_{1}a_{2}\ldots a_{n}} и ±(a0,a1a2…an+10−n){\displaystyle \pm \left(a_{0},a_{1}a_{2}\ldots a_{n}+10^{-n}\right)} для всех n=0,1,2,…{\displaystyle n=0,1,2,\ldots }
Сравнение вещественных чисел в форме бесконечных десятичных дробей производится поразрядно. Например, пусть даны два неотрицательных числа
α=+a0,a1a2…an…β=+b0,b1b2…bn…{\displaystyle {\begin{matrix}\alpha &=+a_{0},a_{1}a_{2}\ldots a_{n}\ldots \\\beta &=+b_{0},b_{1}b_{2}\ldots b_{n}\ldots \end{matrix}}}Если a0<b0{\displaystyle a_{0}<b_{0}}, то α<β{\displaystyle \alpha <\beta }; если a0>b0{\displaystyle a_{0}>b_{0}} то α>β{\displaystyle \alpha >\beta }. В случае равенства a0=b0{\displaystyle a_{0}=b_{0}} переходят к сравнению следующего разряда. И так далее. Если α≠β{\displaystyle \alpha \neq \beta }, то после конечного числа шагов встретится первый разряд n{\displaystyle n}, такой что an≠bn{\displaystyle a_{n}\neq b_{n}}. Если an<bn{\displaystyle a_{n}<b_{n}}, то α<β{\displaystyle \alpha <\beta }; если an>bn{\displaystyle a_{n}>b_{n}} то α>β{\displaystyle \alpha >\beta }.
Однако, при этом следует учитывать, что число a0,a1a2…an(9)=a0,a1a2…an+10−n{\displaystyle a_{0},a_{1}a_{2}\ldots a_{n}(9)=a_{0},a_{1}a_{2}\ldots a_{n}+10^{-n}}. Поэтому если запись одного из сравниваемых чисел, начиная с некоторого разряда, представляет собой периодическую десятичную дробь, у которой в периоде стоит 9, то её следует заменить на эквивалентную запись, с нулём в периоде.
Арифметические операции над бесконечными десятичными дробями определяются как непрерывное продолжение[15] соответствующих операций над рациональными числами. Например, суммой вещественных чисел α{\displaystyle \alpha } и β{\displaystyle \beta } называется вещественное число α+β{\displaystyle \alpha +\beta }, удовлетворяющее следующему условию:
∀a′,a″,b′,b″∈Q(a′⩽α⩽a″)∧(b′⩽β⩽b″)⇒(a′+b′⩽α+β⩽a″+b″){\displaystyle \forall a',a'',b',b''\in \mathbb {Q} \;(a'\leqslant \alpha \leqslant a'')\land (b'\leqslant \beta \leqslant b'')\Rightarrow (a'+b'\leqslant \alpha +\beta \leqslant a''+b'')}Аналогично определяет операция умножения бесконечных десятичных дробей.
Теория сечений в области рациональных чисел[править | править код]
В подходе Дедекинда вещественные числа определяются с помощью сечений в множестве рациональных чисел.
Сечением в множестве рациональных чисел Q{\displaystyle \mathbb {Q} } называется всякое разбиение совокупности всех рациональных чисел на два непустых класса — нижний A{\displaystyle A} и верхний A′{\displaystyle A'}, так что каждое число из нижнего класса строго меньше всякого числа из верхнего:
Q=A∪A′∧A,A′≠∅∧∀a∈A,∀a′∈A′(a<a′){\displaystyle \mathbb {Q} =A\cup A'\quad \land \quad A,A'\neq \varnothing \quad \land \quad \forall a\in A,\forall a'\in A'\;(a<a')}
Если существует число α{\displaystyle \alpha }, которое является максимальным в нижнем классе, либо минимальным в верхнем классе, то это число разделяет множества A{\displaystyle A} и A′{\displaystyle A'}: числа нижнего и верхнего классов лежат по разные стороны от α{\displaystyle \alpha }. Говорят также, что рациональное число α{\displaystyle \alpha } производит данное сечение множества рациональных чисел.
Если же в нижнем классе сечения нет максимального элемента, а в верхнем — минимального, то не существует никакого рационального числа, которое разделяло бы множества A{\displaystyle A} и A′{\displaystyle A'}. В этом случае по определению полагают, что данное сечение определяет некоторое иррациональное число α{\displaystyle \alpha }, которое находится между нижним и верхним классами, и тем самым производит данное сечение. Иначе говоря, для всякого сечения, не производимого никаким рациональным числом, вводят новый объект — иррациональное число, которое по определению больше всякого числа из нижнего класса и меньше всякого числа из верхнего класса:
∀a∈A,∀a′∈A′a<α<a′{\displaystyle \forall a\in A,\forall a'\in A'\;a<\alpha <a'}
Объединение всех рациональных и всех иррациональных чисел называют множеством вещественных чисел, а его элементы — вещественными числами.
Арифметические операции над вещественными числами определяются как непрерывное продолжение соответствующих операций над рациональными числами. Например, суммой вещественных чисел α{\displaystyle \alpha } и
Натуральный ряд Википедия
 Натуральные числа можно использовать для счёта (одно яблоко, два яблока и т. п.)
Натуральные числа можно использовать для счёта (одно яблоко, два яблока и т. п.) Натуральные числа (от лат. naturalis «естественный») — числа, возникающие естественным образом при счёте (например, 1, 2, 3, 4, …[1]). Последовательность всех натуральных чисел, расположенных в порядке возрастания, называется натуральным рядом[2].
Множество натуральных чисел является бесконечным, так как для любого натурального числа n{\displaystyle n} найдётся натуральное число, большее чем n{\displaystyle n}. Отрицательные и нецелые числа к натуральным не относят.
Свойства натуральных чисел и операций с ними изучают арифметика и (более углублённо) теория чисел.
Место нуля[ | ]
Существуют два подхода к определению натуральных чисел:
- числа, возникающие при подсчёте (нумерации) предметов: первый, второй, третий, четвёртый, пятый…;
- числа, возникающие при обозначении количества предметов: 0 предметов, 1 предмет, 2 предмета, 3 предмета, 4 предмета, 5 предметов…
В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля. Не существует единого для большинства математиков мнения о предпочтительности первого или второго подхода (то есть считать ли ноль натуральным числом или нет). В подавляющем большинстве российских источников традиционно принят первый подход[3]. Второй подход, например, применяется в трудах Николя Бурбаки, где натуральные числа определяются как мощности конечных множеств. Наличие нуля облегчает формулировку и доказательство многих теорем арифметики натуральных чисел, поэтому при первом подходе вводится полезное понятие расширенного натурального ряда, включающего ноль[3].
Множество всех натуральных чисел принято обозначать символом N{\displaystyle \mathbb {N} }. Международные стандарты ISO 31-11 (1992 год) и ISO 80000-2 (2009 год) устанавливают следующие обозначения[4]:
Треугольное число — Википедия
Материал из Википедии — свободной энциклопедии
Треугольное число — один из типов фигурных чисел, определяемый как число точек, которые могут быть расставлены в форме правильного треугольника (см. рисунок). Очевидно, с чисто арифметической точки зрения, n-е треугольное число — это сумма n первых натуральных чисел.
Последовательность треугольных чисел Tn{\displaystyle T_{n}} для n=0,1,2,…{\displaystyle n=0,1,2,\ldots } начинается так:
- 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120 … (последовательность A000217 в OEIS)
- Формулы для n-го треугольного числа:
- Tn=12n(n+1){\displaystyle T_{n}={\frac {1}{2}}n(n+1)};
- Tn=1+2+3+⋯+(n−2)+(n−1)+n=∑j=1nj{\displaystyle T_{n}=1+2+3+\dots +(n-2)+(n-1)+n=\sum _{j=1}^{n}j};
- Tn=(n+12){\displaystyle T_{n}={n+1 \choose 2}} — биномиальный коэффициент.
- Например, 1953 — это 62-е треугольное число: T62=62⋅632=1953.{\displaystyle T_{62}={\frac {62\cdot 63}{2}}=1953.}
- Рекуррентная формула для n-го треугольного числа:
- Tn=Tn−1+n{\displaystyle T_{n}=T_{n-1}+n}.
- Если n{\displaystyle n} точек попарно соединить отрезками, то число отрезков будет выражаться треугольным числом:
- Tn−1=n(n−1)2{\displaystyle T_{n-1}={\frac {n(n-1)}{2}}}
- К примеру, если у нас имеется 4 объекта, то мы сможем построить только 4⋅3/2=6{\displaystyle 4\cdot 3/2=6} одиночных связей между объектами.
- Сумма конечного ряда треугольных чисел вычисляется по формуле:
- Sm−1=1+3+6+⋯+(m−1)m2=m3−m6{\displaystyle S_{m-1}=1+3+6+\dots +{\frac {(m-1)m}{2}}={\frac {m^{3}-m}{6}}}.
- Ряд из чисел, обратных треугольным, сходится:
- 1+13+16+110+115+⋯=2∑n=1∞(1n−1n+1)=2{\displaystyle 1+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+\dots =2\sum _{n=1}^{\infty }\left({1 \over n}-{1 \over n+1}\right)=2}
- Известное в мистике «число зверя» (666) является 36-м треугольным. Оно является наименьшим треугольным числом, которое представимо в виде суммы квадратов треугольных чисел[1]: 666=152+212.{\displaystyle 666=15^{2}+21^{2}.}
- Третья линия (диагональ) треугольника Паскаля состоит из треугольных чисел.
Сумма двух последовательных треугольных чисел — это квадратное число (полный квадрат), то есть
- Tn−1+Tn=n2{\displaystyle T_{n-1}+T_{n}=n^{2}}.
Примеры:
6 + 10 = 16 10 + 15 = 25
Каждое чётное совершенное число является треугольным[2].
Любое натуральное число представимо в виде суммы не более трёх треугольных чисел. Утверждение впервые сформулировал в 1638 году Пьер Ферма в письме к Мерсенну без доказательства, впервые доказано в 1796 году Гауссом[3].
Натуральное число m{\displaystyle m} является треугольным тогда и только тогда, когда число 8m+1{\displaystyle 8m+1} является полным квадратом. В самом деле, если m{\displaystyle m} треугольное, то 8m+1=8n(n+1)2+1=4n2+4n+1=(2n+1)2.{\displaystyle 8m+1=8{\frac {n(n+1)}{2}}+1=4n^{2}+4n+1=(2n+1)^{2}.} Обратно, число 8m+1{\displaystyle 8m+1} нечётно, и если оно равно квадрату некоторого числа a,{\displaystyle a,} то a{\displaystyle a} тоже нечётно: a=2c+1,{\displaystyle a=2c+1,} и мы получаем равенство: 8m+1=(2c+1)2=4c2+4c+1,{\displaystyle 8m+1=(2c+1)^{2}=4c^{2}+4c+1,} откуда: m=c(c+1)2{\displaystyle m={\frac {c(c+1)}{2}}} — треугольное число.
Квадрат n-го треугольного числа является суммой кубов n первых натуральных чисел[4].
Существует бесконечно много треугольных чисел, которые одновременно являются квадратными («квадратные треугольные числа»)[5]: 1,36,1225,41616,1413721…{\displaystyle 1,36,1225,41616,1413721\dots } (последовательность A001110 в OEIS).
Понятие плоского треугольного числа можно обобщить на три и более измерений. Пространственным их аналогом служат тетраэдральные числа, а в произвольном d{\displaystyle d}-мерном пространстве можно определить гипертетраэдральные числа:
- Tn[d]=(n−1+d)!(n−1)! d!{\displaystyle T_{n}^{[d]}={\frac {(n-1+d)!}{(n-1)!\ d!}}}
Их частным случаем выступают:
- Tn[2]{\displaystyle T_{n}^{[2]}} — треугольные числа.
- Tn[3]{\displaystyle T_{n}^{[3]}} — тетраэдральные числа.
- Tn[4]{\displaystyle T_{n}^{[4]}} — пентатопные числа.
- ↑ Деза Е., Деза М., 2016, с. 225.
- ↑ Voight, John. Perfect numbers: an elementary introduction // University of California, Berkley. — 1998. — С. 7.
- ↑ Деза Е., Деза М., 2016, с. 10.
- ↑ Деза Е., Деза М., 2016, с. 79.
- ↑ Деза Е., Деза М., 2016, с. 25—33.
- Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М.: Просвещение, 1996. — С. 30. — 320 с. — ISBN 5-09-006575-6.
- Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.
- Деза Е., Деза М. Фигурные числа. — М.: МЦНМО, 2016. — 349 с. — ISBN 978-5-4439-2400-7.
Фигурные числа — Википедия
Фигу́рные чи́сла — числа, которые можно представить с помощью геометрических фигур. Это историческое понятие восходит к пифагорейцам, которые развивали алгебру на геометрической основе; отголоском этого подхода остались выражения «возвести число в квадрат или в куб». В теории чисел и комбинаторике фигурные числа связаны с многими другими классами целых чисел — биномиальными коэффициентами, совершенными числами, числами Мерсенна, Ферма, Фибоначчи, Люка и другими[1].
Со времён пифагорейцев (VI век до н. э.) традиционно различают следующие виды фигурных чисел (они определены, например, в VII книге «Начал» Евклида)[2]:
- Линейные числа — числа, не разлагающиеся на сомножители, бо́льшие единицы, то есть это ряд простых чисел, дополненный единицей (у Евклида используется термин «первые числа», πρώτοι αριθμοί):
- 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271 … (последовательность A008578 в OEIS)
- Плоские числа — числа, представимые в виде произведения двух сомножителей, бо́льших единицы, то есть составные:
- 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88 … (последовательность A002808 в OEIS)
- Частным случаем являются прямоугольные числа (в источниках называются также «продолговатыми»), являющиеся произведением двух последовательных целых чисел, то есть имеющие вид n(n+1).{\displaystyle n(n+1).}
- Телесные числа — числа, представимые произведением трёх сомножителей:
- 8, 12, 16, 18, 20, 24, 27, 28, 30, 32, 36, 40, 42, 44, 45, 48, 50, 52, 54, 56, 60, 63, 64, 66, 68, 70, 72, 75, 76, 78, 80, 81, 84, 88, 90, 92, 96, 98, 99, 100, 102, 104, 105, 108, 110, 112, 114, 116, 117, 120, 124, 125, 126, 128, 130, 132, 135, 136, 138, 140, 144 … (последовательность A033942 в OEIS)
- Многоугольные числа — числа, связанные с определённым многоугольником, определение см. ниже.
- Пространственные многогранные числа — числа, связанные с определённым многогранником, определение см. ниже.
Определение и общий вид[править | править код]
Общее определение k-угольного числа для любого k⩾3{\displaystyle k\geqslant 3} можно сформулировать следующим образом[3]:
| n{\displaystyle n}-е по порядку k-угольное число Pn(k){\displaystyle P_{n}^{(k)}} есть сумма первых n{\displaystyle n} членов арифметической прогрессии, у которой первый член равен 1, а разность равна k−2{\displaystyle k-2}. |
Например, треугольные числа получаются как частичные суммы ряда 1+2+3+4…{\displaystyle 1+2+3+4\dots }, а четырёхугольным (квадратным) числам соответствует ряд 1+3+5+7…{\displaystyle 1+3+5+7\dots }
Последовательность k-угольных чисел имеет вид[4]:
- 1,k,3k−3,6k−8,10k−15,15k−24,21k−35,28k−48,36k−63,45k−80…{\displaystyle 1,k,3k-3,6k-8,10k-15,15k-24,21k-35,28k-48,36k-63,45k-80\dots }
Общую формулу для явного подсчёта n{\displaystyle n}-го по порядку k-угольного числа Pn(k){\displaystyle P_{n}^{(k)}} легко получить, найдя по стандартным правилам сумму арифметической прогрессии. Эту формулу можно представить в нескольких вариантах, получаемых один из другого простыми преобразованиями[5]:
| Pn(k)=n+(k−2)n(n−1)2=(k−2)n2−(k−4)n2=12k(n2−n)−n2+2n{\displaystyle P_{n}^{(k)}=n+(k-2){\frac {n(n-1)}{2}}={\frac {(k-2)n^{2}-(k-4)n}{2}}={\frac {1}{2}}k(n^{2}-n)-n^{2}+2n} | (ОКФ) |
Можно также использовать рекуррентную формулу[5]:
- Pn+1(k)=Pn(k)+(k−2)n+1; P1(k)=1{\displaystyle P_{n+1}^{(k)}=P_{n}^{(k)}+(k-2)n+1;\ P_{1}^{(k)}=1}
При увеличении числа сторон k{\displaystyle k} на единицу соответствующие фигурные числа изменяются согласно формуле Никомаха[6]:
| Pn(k+1)=Pn(k)+Pn−1(3),{\displaystyle P_{n}^{(k+1)}=P_{n}^{(k)}+P_{n-1}^{(3)},} где n>1.{\displaystyle n>1.} | (Никомах) |
Поскольку Pn(k){\displaystyle P_{n}^{(k)}} линейно зависит от k,{\displaystyle k,} справедлива формула:
- Pn(k+s)+Pn(k−s)=2Pn(k){\displaystyle P_{n}^{(k+s)}+P_{n}^{(k-s)}=2P_{n}^{(k)}}, где s=0,1,2…k−3.{\displaystyle s=0,1,2\dots k-3.}
Другими словами, каждое многоугольное число есть среднее арифметическое для равноотстоящих от него по k{\displaystyle k} многоугольных чисел с тем же номером.
Если k{\displaystyle k} — простое число, то второе k-угольное число, равное k,{\displaystyle k,} также простое; это единственная ситуация, когда многоугольное число является простым. В самом деле, запишем общую формулу в следующем виде:
- Pn(k)=2+(n−1)(k−2)2n{\displaystyle P_{n}^{(k)}={\frac {2+(n-1)(k-2)}{2}}n}
Пусть n>2.{\displaystyle n>2.} Если n{\displaystyle n} чётно, то фигурное число делится на n/2,{\displaystyle n/2,} а если нечётно, то делится на (2+(n−1)(k−2))/2.{\displaystyle (2+(n-1)(k-2))/2.} В обоих случаях фигурное число оказывается составным[7].
Исторический очерк[править | править код]
Фигурные числа, по мнению пифагорейцев, играют важную роль в структуре мироздания. Поэтому их изучением занимались многие математики античности: Эратосфен, Гипсикл, Диофант Александрийский и другие. Гипсикл (II век до н. э.) дал общее определение k-угольного числа Pn(k){\displaystyle P_{n}^{(k)}} как суммы n{\displaystyle n} членов арифметической прогрессии, у которой первый член есть 1, а разность равна k−2;{\displaystyle k-2;} определение Гипсикла приводится в книге Диофанта в следующем виде[8][9]:
Если взять сколько-нибудь чисел, начиная с единицы, имеющих одинаковые разности, то сумма их, если разность единица, будет треугольником, если же двойка, то четырёхугольником, а если тройка — пятиугольником. Количество углов определяется разностью, увеличенной на двойку, а сторона — количеством взятых чисел, считая и единицу.
Диофант написал большое исследование о свойствах многоугольных чисел, фрагменты которого дошли до наших дней. О фигурных числах много говорится в пифагорейских учебниках арифметики, созданных Никомахом Геразским и Теоном Смирнским (II век), которые установили ряд зависимостей между фигурными числами разных размерностей. Большой интерес к фигурным числам проявили индийские математики и первые математики средневековой Европы (Фибоначчи, Пачоли, Кардано и др.)[10][1].
В Новое время многоугольными числами занимались Ферма, Валлис, Эйлер, Лагранж, Гаусс и другие. В сентябре 1636 года[11] Ферма сформулировал в письме Мерсенну замечательную теорему, которая сегодня называется теоремой Ферма о многоугольных числах[10]:
Я первым открыл очень красивую и совершенно общую теорему о том, что каждое число является либо треугольным, либо суммой двух или трёх треугольных чисел; каждое число или квадратное, или является суммой двух, трёх или четырёх квадратов; или пятиугольное, или является суммой двух, трёх, четырёх или пяти пятиугольных чисел, и т. д. до бесконечности, будь то для шестиугольных, семиугольных или любых многоугольных чисел. Я не могу дать здесь доказательство, которое зависит от многочисленных и запутанных тайн чисел, ибо я намерен посвятить этой теме целую книгу и получить в этой части арифметики удивительные достижения по сравнению с ранее известными пределами.
Вопреки обещанию, Ферма так и не опубликовал доказательство этой теоремы, которую в письме Паскалю (1654) назвал своим главным достижением в математике[11]. Проблемой занимались многие выдающиеся математики — в 1770 году Лагранж доказал теорему для квадратных чисел (теорема Лагранжа о сумме четырёх квадратов), в 1796 году Гаусс дал доказательство для треугольных. Полное доказательство теоремы сумел дать Коши в 1813 году[12][13].
Треугольные числа[править | править код]
Последовательность треугольных чисел:
- 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, 1326, 1378, 1431 …, n(n+1)2{\displaystyle {\frac {n(n+1)}{2}}} … (последовательность A000217 в OEIS)
Свойства:
- Чётность элемента последовательности меняется с периодом 4: нечётное, нечётное, чётное, чётное.
- Обозначим для краткости n{\displaystyle n}-е треугольное число: Tn=Pn(3)=n(n+1)2.{\displaystyle T_{n}=P_{n}^{(3)}={\frac {n(n+1)}{2}}.} Тогда справедливы рекуррентные формулы[14]:
- T2n=3Tn+Tn−1{\displaystyle T_{2n}=3T_{n}+T_{n-1}}
- T2n+1=3Tn+Tn+1{\displaystyle T_{2n+1}=3T_{n}+T_{n+1}}
| Pn(k)=n+(k−2)n(n−1)2=(k−2)Tn−1+n=(k−3)Tn−1+Tn{\displaystyle P_{n}^{(k)}=n+(k-2){\frac {n(n-1)}{2}}=(k-2)T_{n-1}+n=(k-3)T_{n-1}+T_{n}} | (Баше) |
- Сумма двух последовательных треугольных чисел даёт полный квадрат (квадратное число):
- Tn+Tn+1=(n+1)2=Pn+1(4).{\displaystyle T_{n}+T_{n+1}=(n+1)^{2}=P_{n+1}^{(4)}.}.
- Сумма конечного ряда треугольных чисел вычисляется по формуле:
- Sm−1=1+3+6+⋯+(m−1)m2=m3−m6{\displaystyle S_{m-1}=1+3+6+\dots +{\frac {(m-1)m}{2}}={\frac {m^{3}-m}{6}}}.
- Ряд из чисел, обратных треугольным, сходится:
- 1+13+16+110+115+⋯=2∑n=1∞(1n−1n+1)=2{\displaystyle 1+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+\dots =2\sum _{n=1}^{\infty }\left({1 \over n}-{1 \over n+1}\right)=2}
- Удвоенные треугольные числа дают последовательность (определённых выше [⇨]) прямоугольных чисел.
- Натуральное число N{\displaystyle N} является треугольным тогда и только тогда, когда число 8N+1{\displaystyle 8N+1} является полным квадратом. Это несложно доказать непосредственно, но проще вывести из общей методики (задача 2)..
- Существует бесконечно много треугольных чисел, которые одновременно являются квадратными («квадратные треугольные числа»)[16]: 1,36,1225,41616,1413721…{\displaystyle 1,36,1225,41616,1413721\dots } (последовательность A001110 в OEIS).
- Известное в мистике «число зверя» (666) является 36-м треугольным. Оно является наименьшим треугольным числом, которое представимо в виде суммы квадратов треугольных чисел[17]: 666=152+212.{\displaystyle 666=15^{2}+21^{2}.}
- Треугольные числа образуют третью диагональную линию треугольника Паскаля; см. подробнее ниже.
Квадратные числа[править | править код]
Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами:
- 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500 …, n2{\displaystyle n^{2}} … (последовательность A000290 в OEIS)
Каждое квадратное число, кроме единицы, есть сумма двух последовательных треугольных чисел:
- n2=Tn−1+Tn{\displaystyle n^{2}=T_{n-1}+T_{n}}. Примеры: 4=1+3;9=3+6;16=6+10{\displaystyle 4=1+3;\quad 9=3+6;\quad 16=6+10} и т. д.
Сумма квадратов первых n{\displaystyle n} натуральных чисел вычисляется по формуле[18]:
- 12+22+32+...+n2=n(n+1)(2n+1)6{\displaystyle 1^{2}+2^{2}+3^{2}+...+n^{2}={\frac {n(n+1)(2n+1)}{6}}}
Ряд обратных квадратов сходится[19]:
- ∑n=1∞1n2=112+122+⋯+1n2+⋯=π26{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\dots +{\frac {1}{n^{2}}}+\dots ={\frac {\pi ^{2}}{6}}}
Каждое натуральное число может быть представлено как сумма не более четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов).
Пятиугольные числа[править | править код]
- 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162, 1247, 1335, 1426, 1520, 1617, 1717, 1820, 1926, 2035, 2147, 2262, 2380, 2501, 2625, 2752, 2882, 3015, 3151 …, n(3n−1)2{\displaystyle {\frac {n(3n-1)}{2}}} … (последовательность A000326 в OEIS)
Если в формуле n(3n−1)2{\displaystyle {\frac {n(3n-1)}{2}}} указать для n{\displaystyle n} более общую последовательность:
- n=0,1,−1,2,−2,3,−3…{\displaystyle n=0,1,-1,2,-2,3,-3\dots }
то получатся так называемые обобщённые пятиугольные числа:
- 0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155, 176, 187, 210, 222, 247, 260, 287, 301, 330, 345, 376, 392, 425, 442, 477, 495, 532, 551, 590, 610, 651, 672, 715, 737, 782, 805, 852, 876, 925, 950, 1001, 1027, 1080, 1107, 1162, 1190, 1247, 1276, 1335... (последовательность A001318 в OEIS)
Леонард Эйлер обнаружил обобщённые пятиугольные числа в следующем тождестве:
- (1−x)(1−x2)(1−x3)…=1−x−x2+x5+x7−x12−x15+x22+x26−x35−x40+…{\displaystyle (1-x)(1-x^{2})(1-x^{3})\ldots =1-x-x^{2}+x^{5}+x^{7}-x^{12}-x^{15}+x^{22}+x^{26}-x^{35}-x^{40}+\ldots }
Степени x{\displaystyle x} в правой части тождества образуют последовательность обобщённых пятиугольных чисел[20], См. подробнее: Пентагональная теорема Эйлера.
Шестиугольные числа[править | править код]
- 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780, 861, 946, 1035, 1128, 1225, 1326, 1431, 1540, 1653, 1770, 1891, 2016, 2145, 2278, 2415, 2556, 2701, 2850, 3003, 3160, 3321, 3486, 3655, 3828, 4005, 4186, 4371, 4560 …, 2n2−n{\displaystyle 2n^{2}-n} … (последовательность A000384 в OEIS)
Очевидно, последовательность шестиугольных чисел получается из последовательности треугольных чисел вычёркиванием элементов с чётными номерами: Pn(6)=P2n−1(3).{\displaystyle P_{n}^{(6)}=P_{2n-1}^{(3)}.}
Натуральное число N{\displaystyle N} является шестиугольным тогда и только тогда, когда число 8N+1+14{\displaystyle {\frac {{\sqrt {8N+1}}+1}{4}}} является натуральным. Это несложно доказать непосредственно, но проще вывести из общей методики (задача 2)..
Двенадцатиугольные числа[править | править код]
Двенадцатиугольные числа вычисляются по формуле 5n2−4n{\displaystyle 5n^{2}-4n}:
- 1, 12, 33, 64, 105, 156, 217, 288, 369, 460, 561, 672, 793, 924, 1065, 1216, 1377, 1548, 1729, 1920, 2121, 2332, 2553, 2784, 3025, 3276, 3537, 3808, 4089, 4380, 4681, 4992, 5313, 5644, 5985, 6336, 6697, 7068, 7449, 7840, 8241, 8652, 9073, 9504, 9945 … (последовательность A051624 в OEIS)
В десятичной системе n{\displaystyle n}-ое двенадцатиугольное число заканчивается на ту же цифру, что и само число n{\displaystyle n}.
Определение, является ли заданное число многоугольным[править | править код]
Задача 1 (часто называемая задачей Диофанта): дано натуральное число N>2,{\displaystyle N>2,} требуется определить, является ли оно многоугольным числом Pn(k){\displaystyle P_{n}^{(k)}} и если да, то для каких значений