Базис что это такое
базис — Викисловарь
Морфологические и синтаксические свойства[править]
ба́-зис
Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a по классификации А. А. Зализняка).
Корень: -баз-; суффикс: -ис [Тихонов, 1996].
Произношение[править]
- МФА: ед. ч. [ˈbazʲɪs], мн. ч. [ˈbazʲɪsɨ]
Семантические свойства[править]
Значение[править]
- филос. совокупность исторически определённых производственных отношений, образующих экономическую структуру общества и определяющих характер надстройки ◆ Отсутствует пример употребления (см. рекомендации).
- книжн. исходные данные, основные положения чего-либо; то, на чём базируется что-либо ◆ Отсутствует пример употребления (см. рекомендации).
- экон. совокупность материальных или технических средств, ресурсов; база ◆ Отсутствует пример употребления (см. рекомендации).
- матем. множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
- частичн.: экономика
- основа, основание, фундамент
- база
Антонимы[править]
- —
- —
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
Этимология[править]
Происходит от лат. basis «основание, подножие», далее из др.-греч. βάσις «ход, шаг; основание», от гл. βαίνω «ходить», из праиндоевр. *gwem-. Русск. база встречается со времени Петра I, заимств. через нем. Base или франц. base из лат. Использованы данные словаря М. Фасмера. См. Список литературы.
Фразеологизмы и устойчивые сочетания[править]
Перевод[править]
| Список переводов | |
| |
Библиография[править]
- Ахманова О. С. Словарь омонимов русского языка. — М. : Русский язык, 1986. — 448 с.
Морфологические и синтаксические свойства[править]
| Ед. | базис |
| Ед. об. | базиса |
| Ед. суб. | базисът |
| Мн. | базиси |
| Мн. сов. | базисите |
| Числ. | базиса |
| Зв. | — |
ба-зис
Существительное, мужской род, склонение 7.
Корень: -базис-.
Произношение[править]
Семантические свойства[править]
Значение[править]
- базис (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
- база
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
Этимология[править]
Происходит от лат. basis «основание, подножие», далее из др.-греч. βάσις «ход, шаг; основание», от гл. βαίνω «ходить», из праиндоевр. *gwem-.
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
базис
Существительное.
Корень: -базис-.
Произношение[править]
Семантические свойства[править]
Значение[править]
- базис (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
Происходит от лат. basis «основание, подножие», далее из др.-греч. βάσις «ход, шаг; основание», от гл. βαίνω «ходить», из праиндоевр. *gwem-.
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
базис
Существительное.
Корень: -базис-.
Произношение[править]
Семантические свойства[править]
Значение[править]
- базис (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
Происходит от лат. basis «основание, подножие», далее из др.-греч. βάσις «ход, шаг; основание», от гл. βαίνω «ходить», из праиндоевр. *gwem-.
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
базис
Существительное.
Корень: -базис-.
Произношение[править]
Семантические свойства[править]
Значение[править]
- базис (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
Происходит от лат. basis «основание, подножие», далее из др.-греч. βάσις «ход, шаг; основание», от гл. βαίνω «ходить», из праиндоевр. *gwem-.
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | ба́зис | ба́зиси |
| Р. | ба́зису | ба́зисів |
| Д. | ба́зисові, ба́зису | ба́зисам |
| В. | ба́зис | ба́зиси |
| Тв. | ба́зисом | ба́зисами |
| М. | ба́зисі | ба́зисах |
| Зв. | ба́зисе* | ба́зиси* |
ба́-зис
Существительное, неодушевлённое, мужской род, тип склонения 1a.
Корень: -базис-.
Произношение[править]
Пример произношения
Семантические свойства[править]
Значение[править]
- базис (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
Происходит от лат. basis «основание, подножие», далее из др.-греч. βάσις «ход, шаг; основание», от гл. βαίνω «ходить», из праиндоевр. *gwem-.
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
базис
Существительное.
Корень: -базис-.
Произношение[править]
Семантические свойства[править]
Значение[править]
- базис (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
Происходит от лат. basis «основание, подножие», далее из др.-греч. βάσις «ход, шаг; основание», от гл. βαίνω «ходить», из праиндоевр. *gwem-.
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
БАЗИС - это... Что такое БАЗИС?
множества X - минимальное порождающее его подмножество В. Порождение означает, что применением операций нек-рого класса к элементам получается любой элемент Это понятие связано с понятием зависимости: элементы Xпосредством операций из ставятся в зависимость от элементов В. Минимальность означает, что никакое собственное подмножество не порождает X. Это свойство обусловливает в нек-ром смысле независимость его элементов: никакой элемент не порождается остальными его элементами. Напр., множество всех натуральных чисел имеет Б. единствевг-ный элемент 0 и порождается из него операцией непосредственного следования и ее итерациями; множество всех натуральных чисел порождается операцией умножения из Б., состоящего из всех простых чисел. Базис алгебры кватернионов состоит из четырех элементов если порождающими операциями являются сложение и умножение на действительные числа; если же кроме этих операций используется еще и умножение кватернионов, то Б.
будет состоять лишь из трех элементов (ибо ).
Базис натурального ряда порядка - подпоследовательность множества натуральных чисел с включением 0, к-рая в результате Декретного сложения с собой (операция порождения) дает все Это означает, что каждое натуральное число ппредставимо в виде
где Напр., всякое натуральное число есть сумма четырех квадратов натуральных чисел (теорема Лагранжа), т. е. последовательность квадратов есть Б. порядка 4. Вообще, последовательность степеней натуральных чисел является Б. (теорема Гильберта), порядок к-рого оценивается Виноградова методом. Понятие Б. обобщается на случай произвольных числовых последовательностей, т. е. функций на .
Порождающие множества существуют всегда (тривиально: порождает ), однако минимальность может оказаться принципиально невозможной (подобная ситуация типична для классов , содержащих бес-конечноместные операции, в частности в топологич. структурах, решетках и т. п.). Поэтому условие минимальности заменяется более слабым требованием: Б. есть порождающее множество минимальной мощности. В связи с этим обычно . Вопределяется как параметризованное множество (или семейство), т. е. как функция на множестве индексов со значениями в , причем ; мощность Тиногда наз. базисной размерностью (или рангом) Напр., счетное всюду плотное множество сепарабель-ного топологич. пространства можно считать его .; порождается из операцией замыкания (к-рая, кстати, и в более общих случаях родственна порождению, см. ниже).
Базис топологии топологич. пространства
(база) - Б. совокупности всех открытых подмножеств X;порождение осуществляется объединением элементов
Базис булевой алгебры (двойственный базе в смысле Тарского) - плотное множество (минимальной мощности) в ; порождение из (а тем самым и само ) определяется условием (что равносильно ), где , , - единица , - операция импликации. Аналогично вводится ибазис фильтра , как множество такое, что для любого существует , и .
Большинство частных случаев Б. множества вводится по следующей схеме. Пусть - булеан , т. е. совокупность всех его подмножеств. Порождающим оператором (или оператором замыкания) называется отображение в себя такое, что: если
Элемент порождается множеством , если в частности, порождает , если . Минимальное множество , обладающее этим свойством, и наз. базисом .определенным оператором . Порождающий оператор J имеет конечный тип, если для любых из следует для нек-рого конечного подмножества порождающий оператор обладает свойством замещения, если для любых следует Порождающий оператор конечного типа со свойством замещения определяет на X отношение зависимости, т. е. разбиение на два класса - зависимых и независимых множеств; множество Аназ. зависимым, если для нек-рого , и независимым, если для любого . При этом зависимо (независимо) тогда и только тогда, когда некоторое (любое) непустое конечное подмножество зависимо (независимо).
Для того чтобы множество было Б. множества , необходимо н достаточно, чтобы было независимым порождающим множеством или, иначе, максимальным независимым в множеством.
Если - произвольное независимое множество, а С - порождающее множество, содержащее А, то существует Б. Вв X такой, что В частности, Xвсегда обладает Б., и любые два его Б. равно-мощны.
В алгебраич. системах X важную роль играет понятие так наз. свободного базиса В, характеризующегося следующим свойством: произвольное отображение в любую алгебраич. систему (той же сигнатуры) может быть продолжено до (гомо) морфизма в , пли, что то же самое, для любого (гомо)морфизма и любого множества порождающие операторы удовлетворяют условию:
Алгебрапч. система, имеющая свободный В., наз. свободной.
Типичным примером является базис (унитарного) модуля Mнад кольцом К - свободное семейство элементов из М, порождающее М(см. [3]). Здесь семейство элементов K-модуля Мназ. свободным, если из (где для всех, кроме конечного числа индексов следует для всех , а порождение осуществляется представлением элементов хв виде линейных комбинаций элементов : существует (зависящее от х).множество элементов такое, что для всех, кроме конечного числа индексов t, и имеет место разложение
(т. е. X- линейная оболочка A). Б. Мв этом смысле является его свободным Б. в вышеуказанном смысле; обратное также верно. Так, множество периодов двоякопериодич. функции одного комплексного переменного, являющееся дискретной абелевой группой (и потому модулем над кольцом ). имеет свободный Б., наз. базисом периодов функции ; он состоит из двух так наз. примитивных периодов. Аналогично определяется Б. периодов абелевой функции нескольких комплексных переменных.
В случае, когда К - тело, всякий Б. (в прежнемсмысле) является свободным. Напротив, существуют модули, не имеющие свободного Б.; таковы, напр., неглавные идеалы в области целостности К, рассматриваемой как K-модуль.
Базис векторного пространства X над полем К- (свободный) В. подлежащего Xунитарного модуля. Аналогично, базис алгебры Анад полем К - Б. подлежащего A векторного пространства. Все Б. данного векторного пространства Xимеют одинаковую мощность, равную мощности Т, к-рая наз. его алгебраической размерностью. Каждый элемент представим линейной комбинацией элементов Б. единственным образом. Элементы , являющиеся линейными функционалами на X, наз. компонентами (координатами) в данном Б..
Множество Аявляется Б. в Xтогда и только тогда, когда А - максимальное (относительно включения) свободное множество в X.
Отображение
где , если - значение t-й компоненты хв Б. A и 0 в противном случае, наз. базисным отображением; оно является линейным инъективным отображением Xв пространство функций на Тсо значениями в K. В данном случае образ состоит из функций с конечным числом значений, отличных от нуля (конечнозначных функций). Эта интерпретация позволяет определить обобщенный базис векторного пространства над полем как биективное линейное отображение его на нек-рое подпространство пространства функций на со значениями в , где - нек-рое надлежащим образом подобранное множество. Однако без введения дополнительных ограничений на (напр., порядка) и структур на (напр., топологии) и согласованных с этим условий на понятие обобщенного Б. практически мало полезно.
Иногда Б. векторного пространства наз. алгебраическим базисом (чем подчеркивается отсутствие связи с дополнительными структурами на , даже если они и согласованы с его векторной структурой).
Базис Гамеля (Хамеля) - Б. поля действительных чисел R, рассматриваемого как векторное пространство над полем рациональных чисел. Введен Г. Гамелем [4] для получения разрывного решения функционального уравнения ; график решения его всюду плотен на плоскости . Каждой почти периодич. функции соответствует нек-рый счетный базис Гамеля такой, что каждый показатель Фурье этой функции принадлежит линейной оболочке . При этом элементы можно выбрать принадлежащими последовательности ; множество наз. базисом почтп периодической функции. Аналогичный Б. строится в кольце, содержащем тело Ри имеющем единицу тела Рсвоей единицей. Алгебраич. Б. произвольного векторного пространства также наз. иногда базисом Гамеля.
Базис топологический (Б. топологического векторного пространства Xнад полем К) - семейство , свойства и функции к-рого аналогичны свойствам н функциям алгебраич. Б. векторного пространства. Понятие топологич. В.- одно из важнейших в функциональном анализе - расширяет и углубляет понятие алгебраич. Б. с учетом топологич. структуры X и позволяет получать для каждого элемента его разложение по Б. и притом единственное, т. е. представление хв виде предела (в том или ином смысле) линейных комбинаций элементов : где - линейные функционалы на Xсо значениями в К, наз. компонентами х в Б . А, или коэффициентами разложениям по Б. А. Очевидно, для существования разложения любого хнеобходимо, чтобы Абыло полным множеством в X, а для единственности такого разложения (т. е. для того, чтобы нулевой элемент Xимел все компоненты равными нулю) необходимо, чтобы Абыло топологическим свободным множеством в X.
Смысл и практич. значение топологич. Б. (наз. далее просто Б.) заключается в установлении биективного линейного отображения X, наз. базисным отображением , на нек-рое, зависящее от X, пространство функций со значениями в К, определенных на (топологическом) пространстве Т, а именно:
где , так что символически и ; при этом строение вследствие конкретности, эффективности своего определения проще и обозримее, чем строение абстрактно заданного . Так, напр., алгебраич. Б. бесконечномерного банахова пространства несчетен, в то время как в ряде случаев при надлежащем обобщении понятия Б. мощность существенно уменьшается, одновременно упрощается и .
Пространство содержит все конечнозначные функции, и множество элементов Б. является биективным прообразом множества функций , имеющих лишь одно ненулевое значение, равное 1 ("однозначных" функций): где при . Другими словами, - образующая одномерного подпространства , дополнительного в Xк гиперплоскости, определяемой уравнением
Таким образом, роль Б. сводится к организации из множества компонент , составляющих образ хпри базисном отображении, суммируемого (в том или ином смысле) семейства , т. е. Б. "разлагает" пространство Xв (обобщенную) прямую сумму одномерных подпространств:
Аналогичным образом определяется Б. в векторных пространствах, наделенных равномерной, предельной (псевдотопологической), линейной , близостной и другими дополнительными структурами.
Мыслимы (и существуют) обобщения понятия Б., идущие в различных направлениях. Так, введение топологии и меры на Тприводит к понятию так наз. непрерывной суммы элементов из Xи соответствующим интегральным представлениям; разложение пространства Xна необязательно одномерные компоненты находит применение в спектральной теории линейных операторов; рассмотрение вместо К(Т).произвольных топологич. алгебр над полем К(напр., алгебры мер на Тсо значениями в Кили даже в X, алгебры проекторов и т. д.) позволяет конкретизировать многие понятия абстрактной двойственности для топологич. векторных пространств и, в частности, использовать развитый аппарат теории характеров.
Базис счетный- наиболее исследованный (и в то же время практически наиболее важный) пример Б.- последовательность элементов пространства Xтакая, что каждому элементу ходнозначно соответствует разложение его в ряд по Б.
сходящийся (в топологии X).к х. Здесь причем существен естественный порядок в нем. Часто счетный Б. наз. просто Б. [Аналогично, если подразумевается слабая сходимость разложения х, определяется слабый счетный базис.] Так, напр., функции , образуют Б. в пространствах (абсолютно суммируемых в степени рпериодич. функций), напротив, в пространствах (измеримых функций, совпадающих почти всюду с ограниченными функциями) и (непрерывных периодич. функций) эти функции Б. не образуют. Необходимым (но далеко не достаточным) условием существования счетного Б. является сепарабельность (напр., в пространстве измеримых на отрезке функций со значениями в счетного Б. быть не может). Впрочем, пространство ограниченных последовательностей, не будучи сепарабельным в топологии , не обладает счетным Б., однако элементы , где при и при , образуют Б. в слабой топологии . Вопрос о существовании счетного Б. в сепарабельных банаховых пространствах (проблема базиса) решен отрицательно [6]. Аналогичный вопрос для ядерных пространств также решен отрицательно [7].
Счетный Б., однако, не всегда оказывается "достаточно хорошим" для применений (напр., компоненты не являются непрерывными, разложение не сходится безусловно и т. п.), в связи с чем на Б. накладываются некоторые условия или вводится надлежащее его обобщение.
Базис счетного типа - одно из обобщений понятия счетного В., для к-рого хотя и несчетно, но разложение элемента по нему естественно определяется: соответствующее пространство состоит из счетнозначных функций. Напр., полное орто-нормированное множество в гильбертовом пространстве Нявляется Б.; если , то (где - скалярное произведение в Н).для всех, за исключением быть может счетного множества, индексов , и ряд сходится к х. Базисное отображение определяется ортогональным проектированием на замкнутые подпространства, порожденные элементами Б. пространства всех комплекснозначных почти периодич. функций на состоит из функций ; здесь - совокупность счетнозначных функций, а базисное отображение определяется формулой
Базис безусловный- счетный Б. в пространстве Xтакой, что разложение любого элемента хсходится безусловно (т. (последовательностей, сходящихся к нулю) и (последовательностей, суммирую мых в степени ) элементы образуют безусловный Б.; в пространстве непрерывных на отрезке функций (любой) Б. не может быть безусловным. Ортонормированный счетный Б. гильбертова пространства - безусловный Б. Банахово пространство с безусловным Б. слабо полно (соответственно обладает сепарабельным сопряженным пространством) в том и только в том случае, когда оно не содержит подпространства, изоморфного с 0 (соответственно ).
Б. и соответствующих банаховых пространств Xи Yназ. эквивалентными, если существует биективное линейное отображение Т:, распространяемое до изоморфизма Xв Y;эти Б. наз. квазиэквивалентными, если они становятся эквивалентными после нек-рой перестановки и нормировки элементов одного из них. Пространства обладают тем свойством, что в каждом из них все нормированные безусловные Б. эквивалентны. В декартовом произведении квазиэквивалентны все безусловные Б. Существуют, однако, нормированные Б., не эквивалентные ортонормированному.
Базис суммирующий - обобщение понятия безусловного Б., соответствующее множеству Тпроизвольной мощности и совпадающее с ним при , - семейство такое, что для любого элемента существует семейство линейных комбинаций (частичных сумм) элементов из А, называемое обобщенным разложением х, суммируемое к х:для любой окрестности нуля найдется конечное подмножество такое, что для каждого конечного множества имеет место
т. е. когда частичные суммы образуют систему (фильтр) Коши. Так, напр., любой ортонормированный Б. гильбертова пространства является суммирующим Б. Аналогично определяется слабый суммирующий базис. Вполне суммирующий базис- такой суммирующий Б., что существует ограниченное множестве Втакое, что множество полунорм суммируемо. Вполне суммирующий Б. не более чем сче-тен. В дуально ядерном пространстве каждый слабо суммирующий Б. вполне суммирующий.
Базис абсолютный (абсолютно суммирующий базис) - суммирующий Б. локально выпуклого пространства над нормированным полем такой, что для каждой окрестности нуля и для каждого суммируемо семейство полунорм Всякий безусловный счетный Б. абсолютен, т. е. ряд сходится для всех и всех непрерывных полунорм . Среди банаховых пространств абсолютным счетным Б. обладают только пространства l1. Если пространство Фреше имеет абсолютный Б., то все его безусловные Б. абсолютны. В ядерных пространствах Фреше каждый счетный Б. (если он существует) абсолютный [13].
Базис Шаудера - Б. пространства Xтакой, что определенное им Оазисное отображение непрерывно [и, следовательно, является изоморфизмом на нек-рое пространство К(Т)], т. е. Б., в к-ром компоненты для любого и, в частности, коэффициенты разложения по этому Б., являются непрерывными функционалами на . Определен впервые Ю. Шаудером [5] для случая . Понятие базиса Шаудера является важнейшим среди всех модификаций понятия Б.
Базис Шаудера Характеризуется тем, что и образуют биортогональную систему. Напр., в пространствах последовательности образуют счетный базис Шаудера. В пространстве счетный базис Шаудера образует Хаара система. В полных метрич. векторных (в частности, банаховых) пространствах всякий счетный Б. является базисом Шаудера [10]. В пространствах Фреше понятия слабого Б. и базиса Шаудера совпадают [11]. В бочечных пространствах, в к-рых нет вообще линейных непрерывных функционалов [8], не существует и базиса Шаудера. Однако, если в них существует слабый базис Шаудера, то он является (обычным) базисом Шаудера [9]. Рефлексивность бочечного локально выпуклого пространства со счетным базисом Шаудера имеет место тогда и только тогда, когда этот Б. является одновременно натягивающим, т. е. если для него будет Б. в сопряженном пространстве , и ограниченно полным, т. е. если ограниченность множества частных сумм ряда влечет сходимость этого ряда [12]. Если базис Шаудера является безусловным Б. в банаховом пространстве, то он тогда и только тогда является натягивающим (соответственно ограниченно полным), когда в Xнет подпространств, изоморфных (соответственно с 0).
Базис Шаудера в локально выпуклом пространстве равностепенно непрерывен, если для каждой окрестности нуля Uнайдется окрестность нуля Vтакая, что для всех . Каждый базис Шаудера бочечного пространства равностепенно непрерывен, и каждое полное локально выпуклое пространство со счетным равностепенно непрерывным Б. отождествимо с некоторым пространством последовательностей [15]. Равностепенно непрерывный Б. ядерного пространства абсолютен.
Лит.: [1] Кон П., Универсальная алгебра, пер. с англ., М., 1968; [2] Мальцев А. И., Алгебраические системы, М., 1970; [3] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [4] Ham el G., "Math. Ann.", 1905, Bd 60, S. 459-62; [5] Sсhaudеr J., "Math. Z.", 1927, Bd 26, S. 47-65, 417-31; [6] Энфло П., "Математика", 1974, т. 18, № 1, с. 146- 155; [7] Зобин Н. М., Митягин Б. С., "Функциональный анализ и его приложения", 1974, т. 8, № 4, с. 35 - 47; [8] Эдвардс Р. .81 - 115; [10] Arsov M. G., "Pacific J. Math.", I960, t. 10, p. 365-79; [11] Bessaga C., Pelezynski A., "Studia Math.", 1960, v. 19, p. 53-62; [12] James R. C., "Ann. Math.", 1950, V. 52, № 2, p. 518-27; [13] Дынин А. С., Митягин Б. С., "Bull. Acad. Polon. Sci.", (Ser. Sci math.), 1960, t. 8, p. 535-40; [14] Дэй М. М., Нормированные линейные пространства, пер. с англ., М., 1961;[15] Пич А., Ядерные локально выпуклые пространства, пер. с нем., М., 1967.
М. И. Войцеховский, М. И. Кадец.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
Понятие базиса.
11
Определение. Три линейно независимых вектора  ,
, 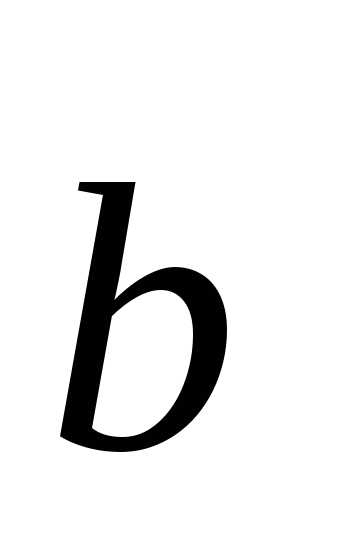 и
и  образуют в пространстве базис, если любой вектор
образуют в пространстве базис, если любой вектор  может быть представлен в виде некоторой линейной комбинации векторов
может быть представлен в виде некоторой линейной комбинации векторов  ,
, 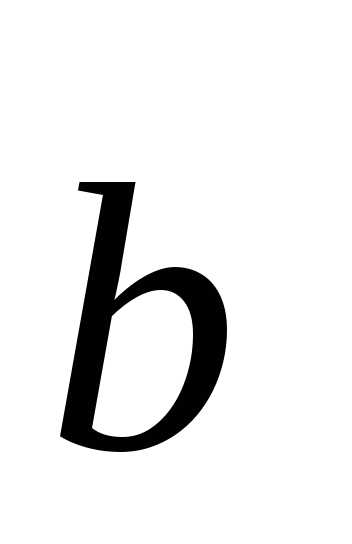 и
и  , т.е. если для вектора
, т.е. если для вектора  найдутся такие вещественные числа , , , что справедливо равенство:
найдутся такие вещественные числа , , , что справедливо равенство:  =
= +
+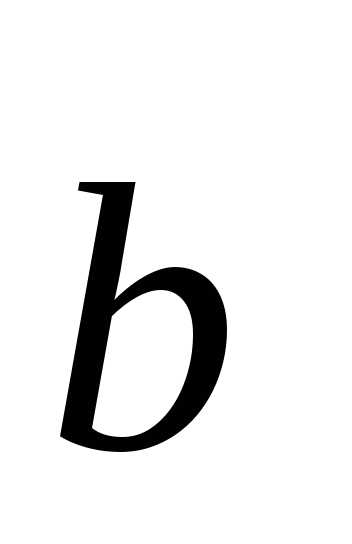 +
+ (1)
(1)
Определение. Два лежащих в плоскости линейно независимых вектора  и
и 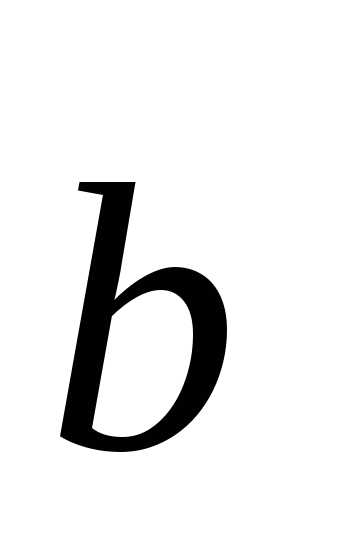 образуют на этой плоскости базис, если любой лежащий в плоскости вектор
образуют на этой плоскости базис, если любой лежащий в плоскости вектор  может быть представлен в виде некоторой линейной комбинации векторов
может быть представлен в виде некоторой линейной комбинации векторов  и
и 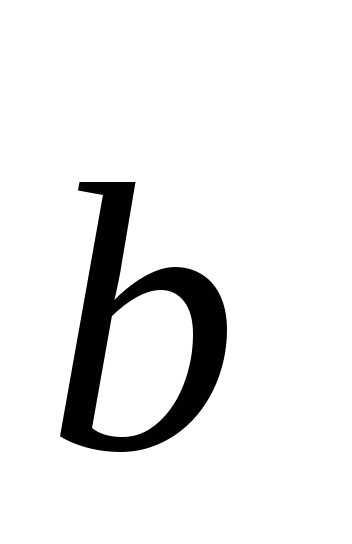 , т.е. если для любого лежащего в плоскости вектора
, т.е. если для любого лежащего в плоскости вектора  найдутся такие вещественные числа и , что справедливо равенство :
найдутся такие вещественные числа и , что справедливо равенство :  =
= +
+ (2)
(2)
Утверждения.
1) любая тройка некомпланарных векторов  ,
,  и
и  образует базис в пространстве;
образует базис в пространстве;
2) любая пара лежащих в данной плоскости неколлинеарных векторов  и
и  образует базис на этой плоскости.
образует базис на этой плоскости.
В дальнейшем для определенности будем рассматривать базис в пространстве.
Пусть  ,
,  и
и  - произвольный базис в пространстве (т.е. произвольная тройка некомпланарных векторов). Тогда равенство
- произвольный базис в пространстве (т.е. произвольная тройка некомпланарных векторов). Тогда равенство  =
= +
+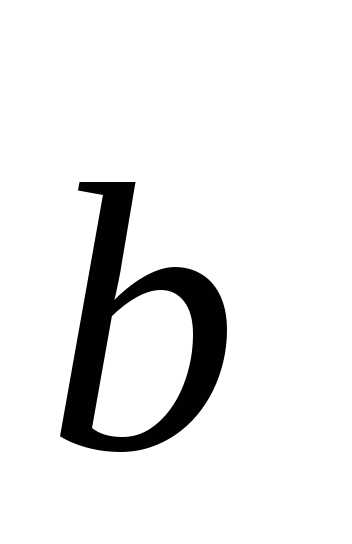 +
+ называется разложением вектора
называется разложением вектора  по базису
по базису  ,
, 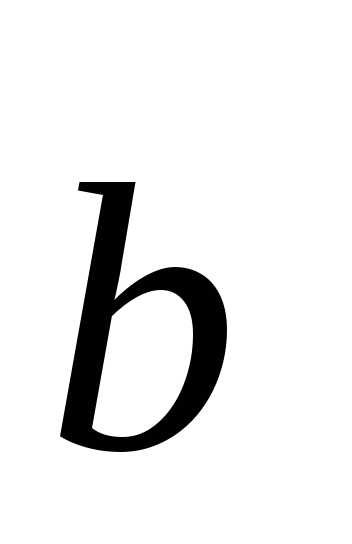 ,
,  , а числа , , - координаты вектора
, а числа , , - координаты вектора  относительно базиса
относительно базиса  ,
, 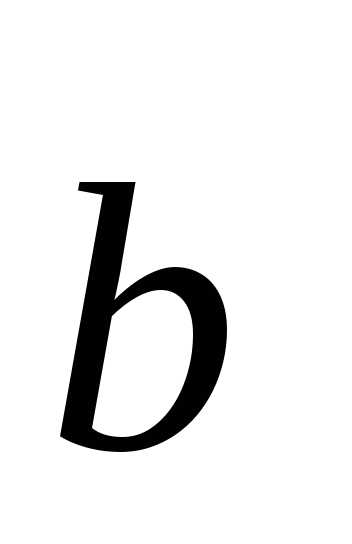 ,
,  .
.
Покажем единственность разложения вектора  по базису
по базису  ,
, 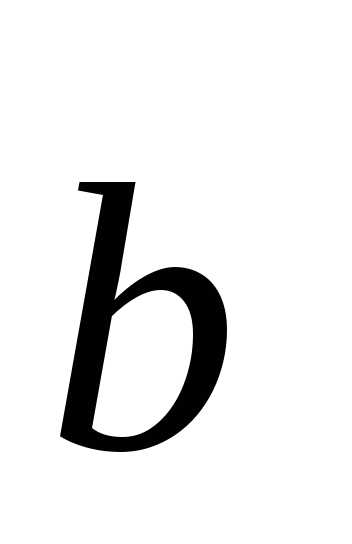 ,
,  . Допустим противное, что наряду с разложением (1), справедливо еще и другое разложение по этому же базису:
. Допустим противное, что наряду с разложением (1), справедливо еще и другое разложение по этому же базису:  =
= +
+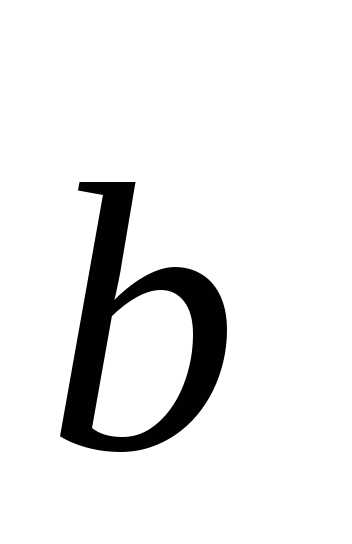 +
+ (3)
(3)
Вычитая из (1) из (3) получаем:
(-) +(-)
+(-)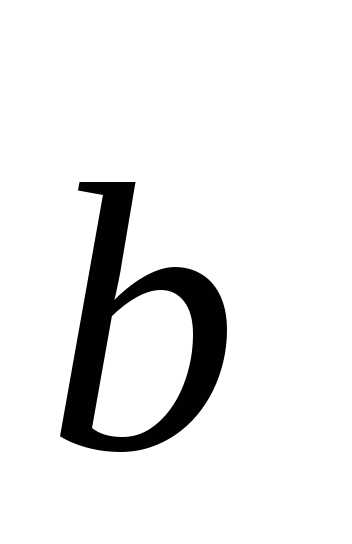 +(-)
+(-) =0
=0
В силу линейной независимости базисных векторов  ,
, 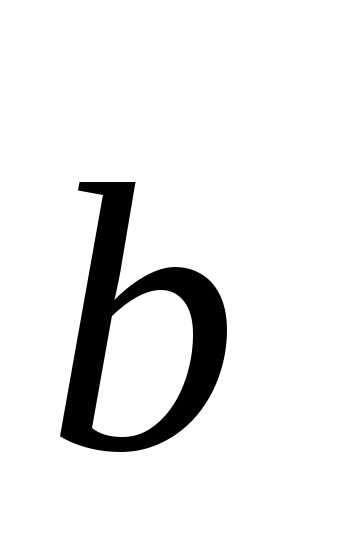 ,
,  последнее соотношение приводит к равенству: -=0, -=0, -=0 или =, =, =.
последнее соотношение приводит к равенству: -=0, -=0, -=0 или =, =, =.
Теорема. При сложении двух векторов 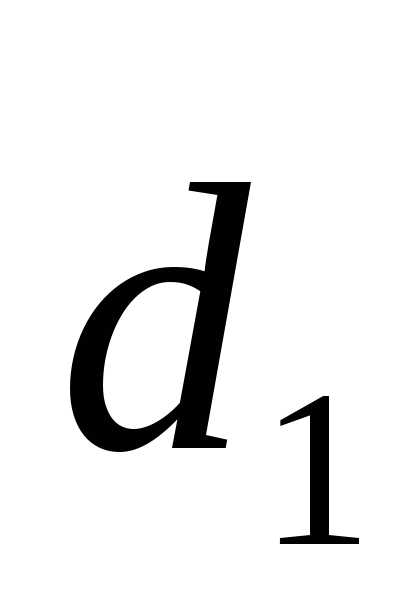 и
и 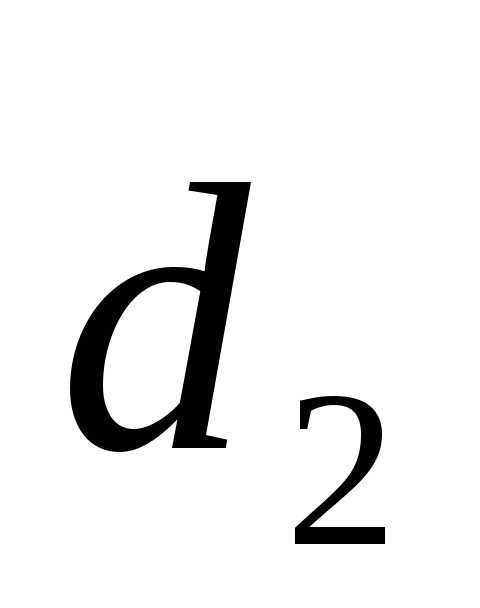 их координаты (относительно любого базиса
их координаты (относительно любого базиса  ,
, 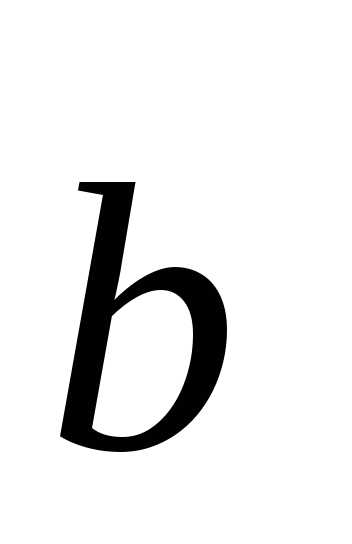 ,
,  ) складываются. При умножении вектора
) складываются. При умножении вектора 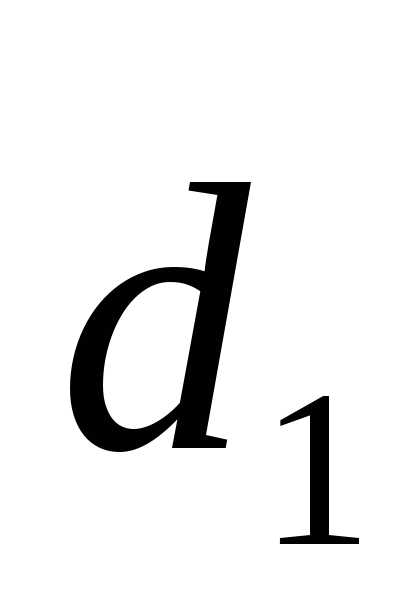 на любое число все его координаты умножаются на это число.
на любое число все его координаты умножаются на это число.
Доказательство. Пусть 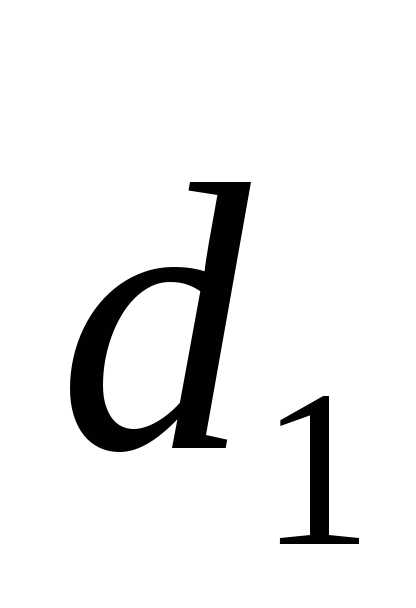 =1
=1 +1
+1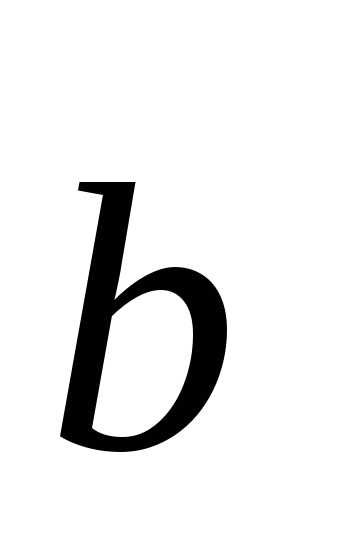 +1
+1 ,
, 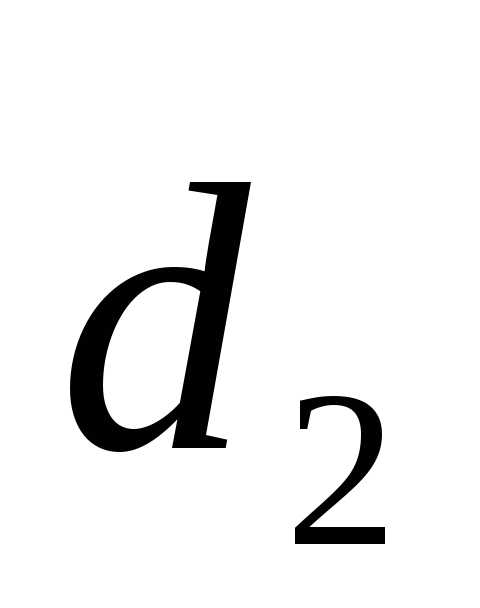 =2
=2 +2
+2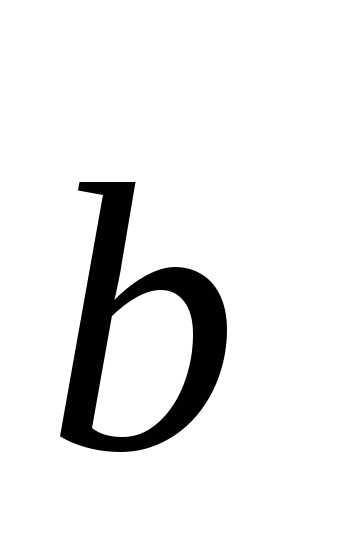 +2
+2 . Тогда в силу свойств линейных операций:
. Тогда в силу свойств линейных операций:
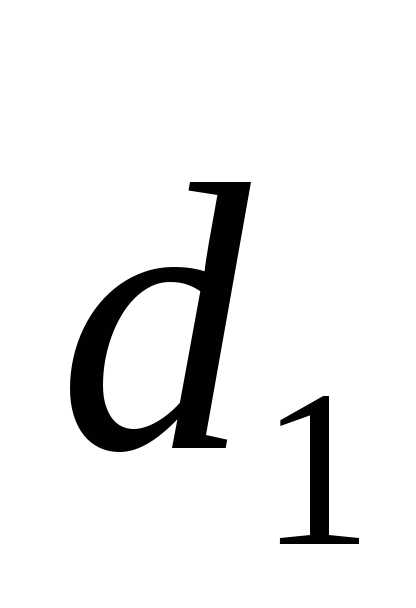 +
+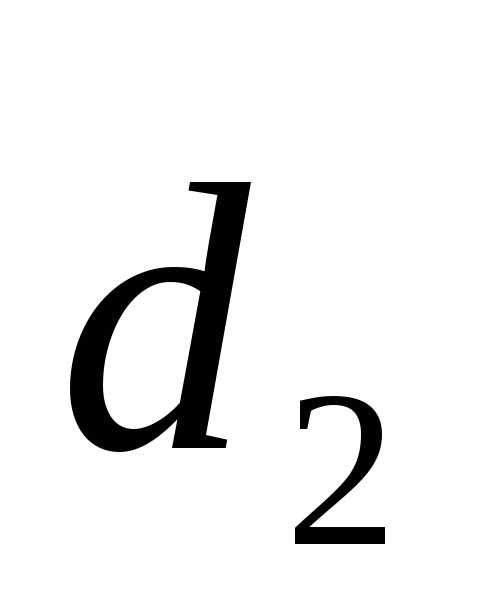 =(1+2)
=(1+2) +(1+2)
+(1+2)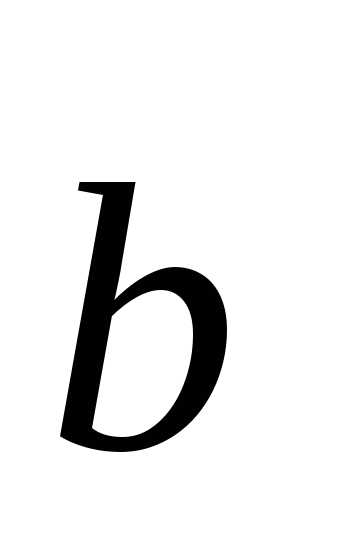 +(1+2)
+(1+2) ,
,
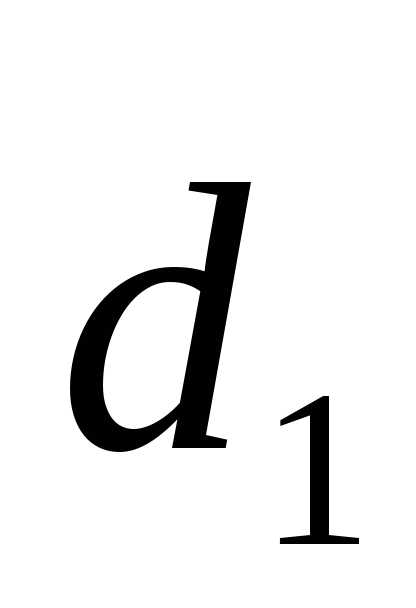 =(1)
=(1) +(1)
+(1)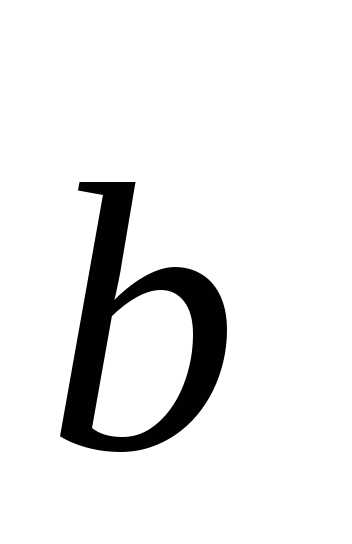 +(1)
+(1)
В силу единственности разложения по базису ч.т.д.
Проекция вектора на ось.
(Ортогональная) проекция точки на ось – основание перпендикуляра, опущенного из точки на данную ось. (рисунок)
П
l
роекцией вектора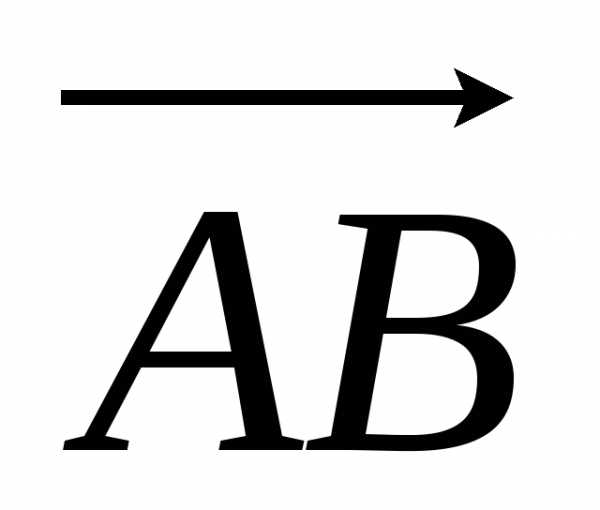 на ось u называется величина (длина) вектора
на ось u называется величина (длина) вектора 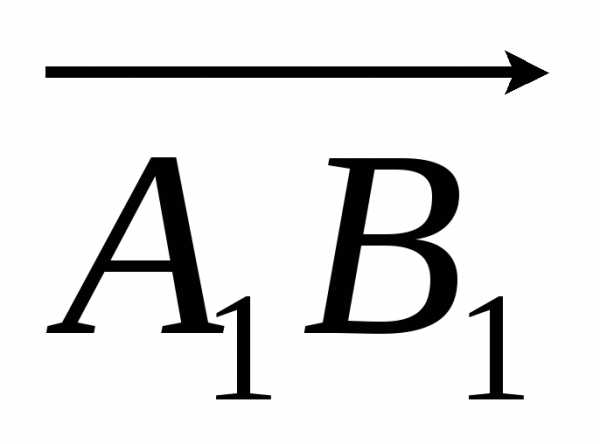 , проведенного из проекции начала в проекцию конца вектора
, проведенного из проекции начала в проекцию конца вектора 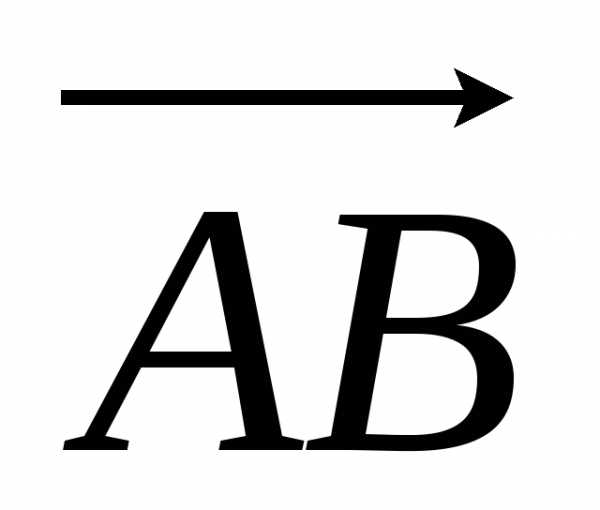 , взятая со знаком “+”, если направление вектора
, взятая со знаком “+”, если направление вектора 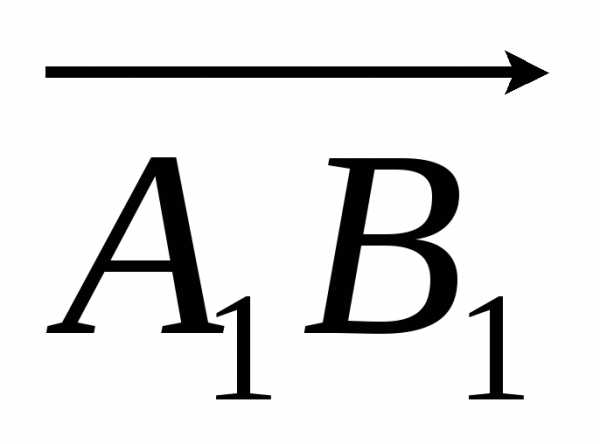 совпадает с направлением оси u и со знаком “-” в противном случае.
совпадает с направлением оси u и со знаком “-” в противном случае. Свойства проекции вектора на ось.
-
Проекция суммы (разности) двух векторов равна сумме (разности) проекций векторов на ось
прu(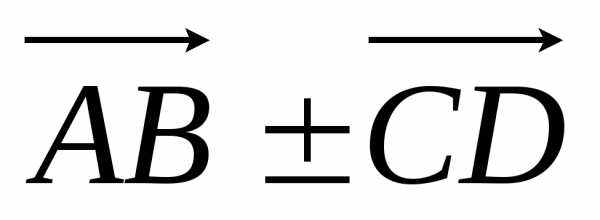 )=
)=
-
Постоянный множитель можно выносить за знак проекции:
Угол наклона вектора  =
=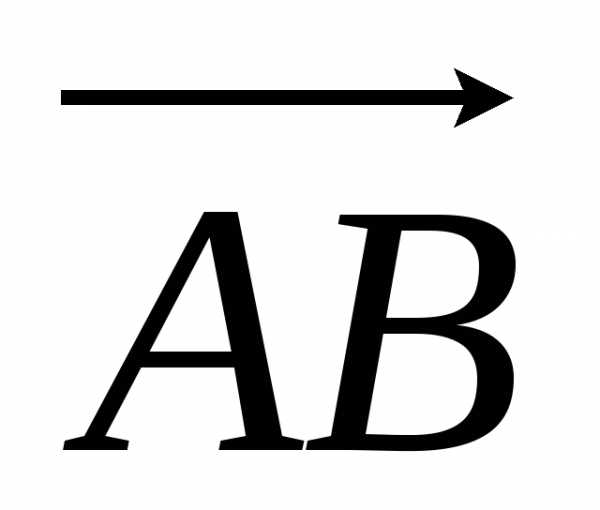 к оси u определяется как угол между двумя выходящими из произвольной точки М лучами, один из которых имеет направление, совпадающее с направлением вектора
к оси u определяется как угол между двумя выходящими из произвольной точки М лучами, один из которых имеет направление, совпадающее с направлением вектора  =
= , а другой – направление, совпадающее с направлением оси u. (Рисунок)
, а другой – направление, совпадающее с направлением оси u. (Рисунок)
На величину угла наклона вектора  к оси u не влияют выбор точки М выхода указанных лучей и замена оси u любой другой осью v, имеющей то же направление, что и ось u.
к оси u не влияют выбор точки М выхода указанных лучей и замена оси u любой другой осью v, имеющей то же направление, что и ось u.
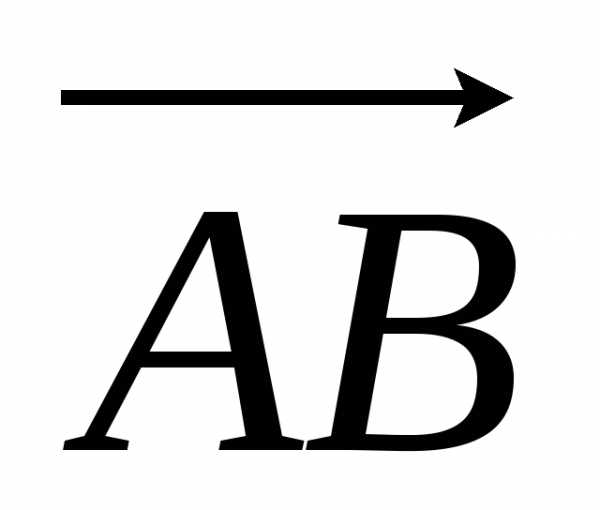
Теорема. Проекция вектора  на ось u равна произведению длины
на ось u равна произведению длины  на косинус угла φ наклона вектора
на косинус угла φ наклона вектора  к оси u: .
к оси u: .
Доказательство. Обозначим через v ось, проходящую через начало А вектора  и имеющую то же направлении, что ось u, и пусть С – проекция В на ось v. Тогда ВАС=, где - угол наклона вектора
и имеющую то же направлении, что ось u, и пусть С – проекция В на ось v. Тогда ВАС=, где - угол наклона вектора  =
=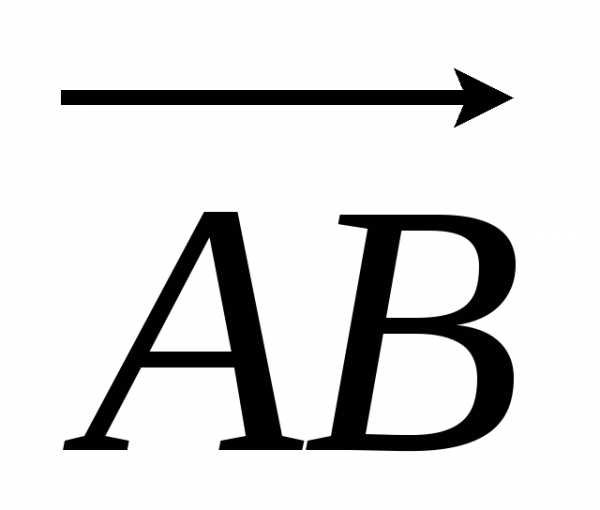 к любой из осей u или v, причем точка С лежит в указанной проецирующей плоскости (т.е. в плоскости, перпендикулярной оси u и проходящей через точку В). (Рисунок)
к любой из осей u или v, причем точка С лежит в указанной проецирующей плоскости (т.е. в плоскости, перпендикулярной оси u и проходящей через точку В). (Рисунок)
А1В1=АС (А1В1–величина вектора 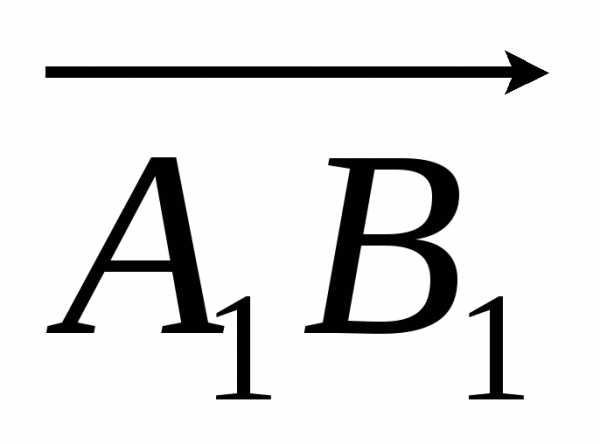 оси u, а АС–величина вектора
оси u, а АС–величина вектора 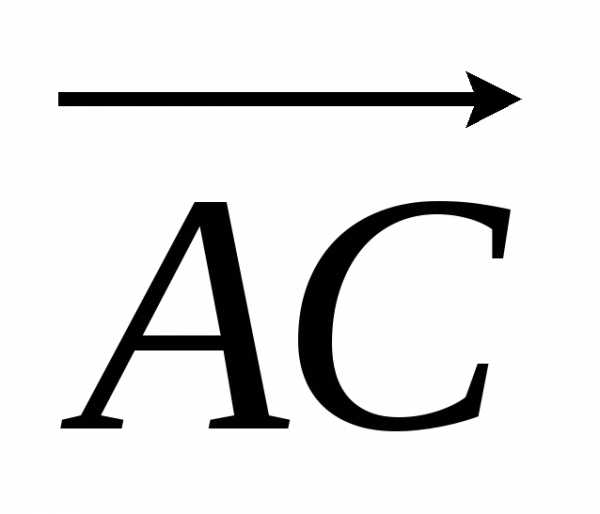 оси v), т.к. оси u и v параллельны и одинаково направлены и отрезки этих осей заключенные между параллельными плоскостями и , равны. Т.к. по определению , то получаем равенство:
оси v), т.к. оси u и v параллельны и одинаково направлены и отрезки этих осей заключенные между параллельными плоскостями и , равны. Т.к. по определению , то получаем равенство: 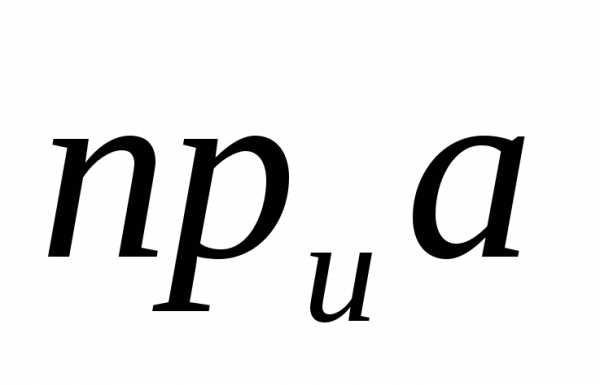 =АС (1)
=АС (1)
Но величина АС представляет собой проекцию вектора 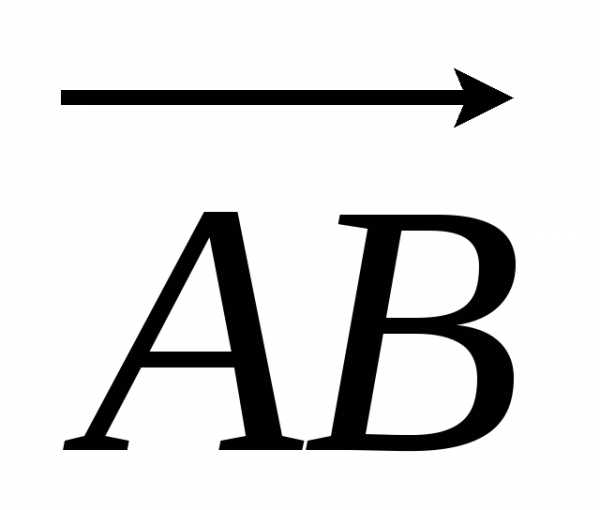 на ось v и
на ось v и
АС=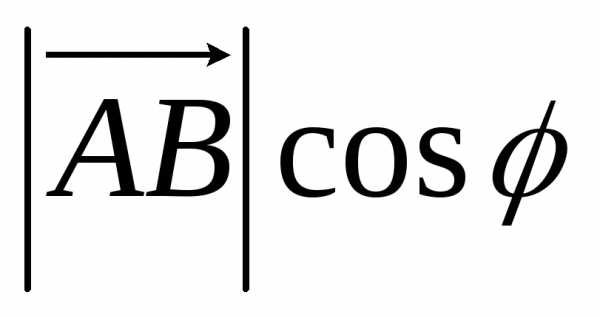 =
= (2)
(2)
Сопоставляя 91) и (20, получим ч.т.д.
Аффинные координаты (от лат. affinis – соседний, смежный).
Аффинные координаты в пространстве определяются заданием базиса  ,
,  ,
,  и некоторой точкой О, называемой началом координат.
и некоторой точкой О, называемой началом координат.
Аффинными координатами любой точки М называются координаты вектора 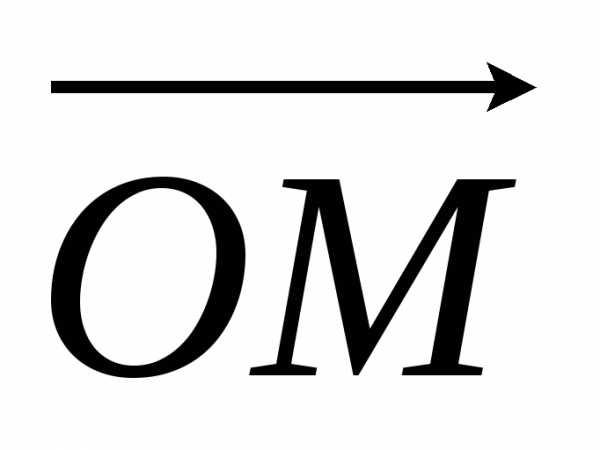 (относительно базиса
(относительно базиса  ,
, 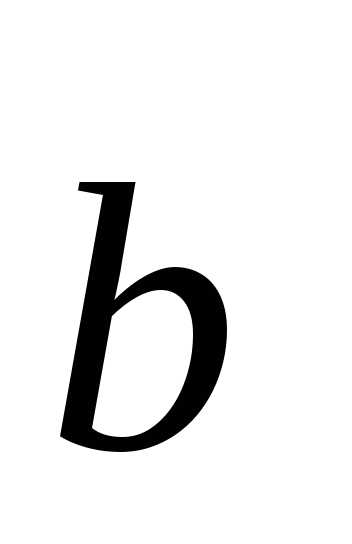 ,
,  ). Т.к. каждый вектор
). Т.к. каждый вектор  может быть единственным образом разложен по базису ,
может быть единственным образом разложен по базису , 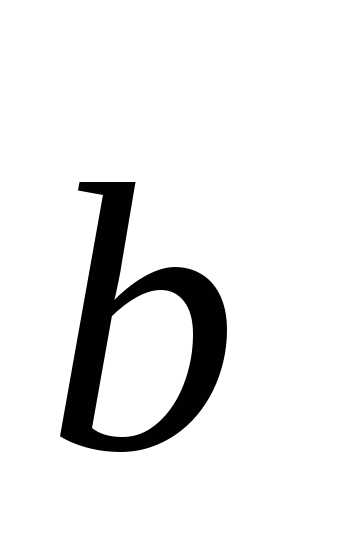 ,
,  , то каждой точке пространства М однозначно соответствует тройка аффинных координат , , .
, то каждой точке пространства М однозначно соответствует тройка аффинных координат , , .
Декартова прямоугольная система координат является частным случаем аффинной системы координат, отвечающей тройке взаимно ортогональных единичных базисных векторов.
Ох – ось абсцисс, Оу – ось ординат, Оz – ось аппликат.
Базисные векторы принято обозначать 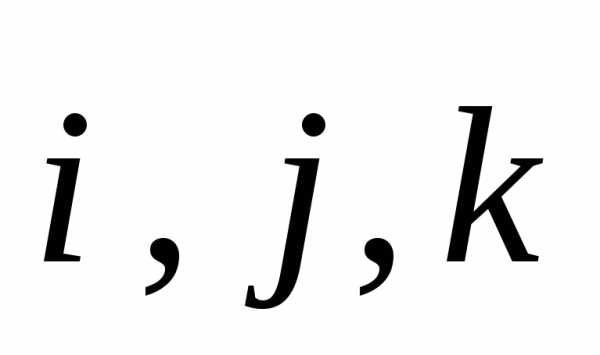 - три взаимно ортогональных единичных вектора.
- три взаимно ортогональных единичных вектора.
Любой вектор  (
( ) можно единственным образом разложить по декартовому базису с коэффициентами ах, ay, az (X,Y,Z):
) можно единственным образом разложить по декартовому базису с коэффициентами ах, ay, az (X,Y,Z):
.
Коэффициенты ах, ay, az называются декартовыми прямоугольными координатами вектора  в базисе
в базисе 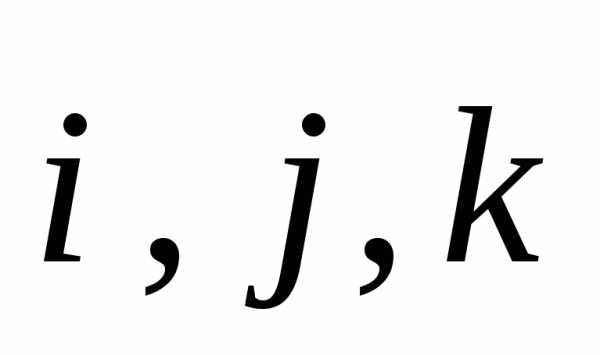 .
.
Если М – любая точка пространства, то декартовы координаты этой точки совпадают с декартовыми координатами вектора 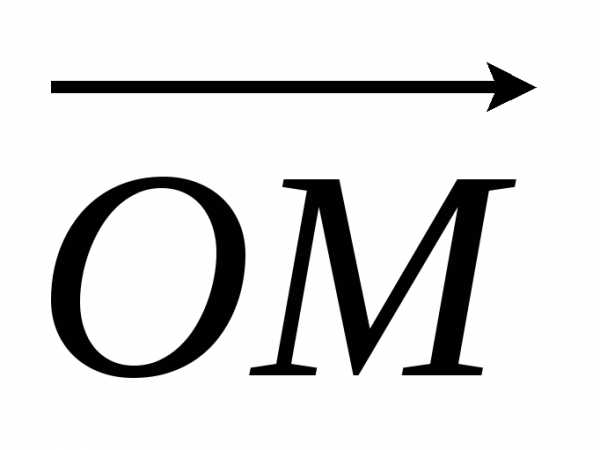 .
.
Координатами вектора  называют координаты его конечной точки. (на рис. коорд. вектора
называют координаты его конечной точки. (на рис. коорд. вектора  =
=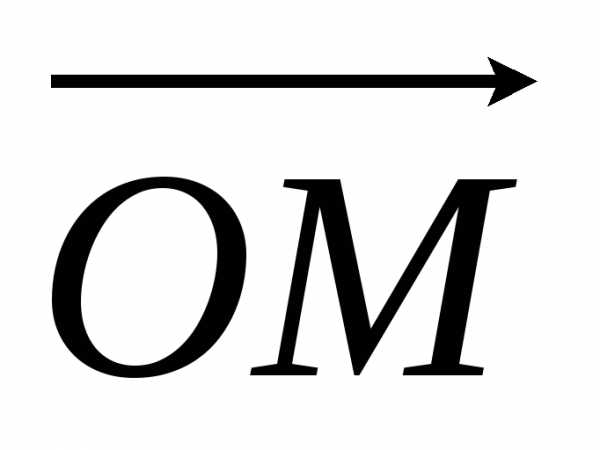 на плоскости
на плоскости  ={х,у}, в пространстве -
={х,у}, в пространстве -  ={x,y,z}).
={x,y,z}).
Теорема. Декартовы прямоугольные координаты X,Y,Z вектора  равны проекциям этого вектора на оси Ox, Oy, Oz.
равны проекциям этого вектора на оси Ox, Oy, Oz.
(Доказательство на стр. 61)
БАЗИС - это... Что такое БАЗИС?
БАЗИС — разница (премия или скидка) между ценой наличного товара и то вара с поставкой на срок, между ценой по сделкам с реальным товаром и биржевыми котировками. Обычно указывается в пунктах вверх или вниз отбиржевой котировки. Используется при… … Финансовый словарь
базис — См … Словарь синонимов
БАЗИС — (греч. basis основание) основа, основание; опора, фундамент, база. Напр., базис колонны, базис программы … Большой Энциклопедический словарь
БАЗИС — БАЗИС, базиса, муж. (греч. basis основание, пьедестал). 1. То же, что база в 1 знач. (архит.). Базис колонны. 2. только ед. То же, что база во 2 знач. (книжн.). Подвести базу подо что н: (твердо обосновать что нибудь, подтвердить что нибудь… … Толковый словарь Ушакова
БАЗИС — (греч. basis) надбавка к биржевой котировке или скидка с нее, являющаяся предметом торга. Она зависит от сорта и качества товара, условий поставки, платежей и др. факторов. Увеличивающийся базис указывается в пунктах вверх от биржевой котировки,… … Экономический словарь
базис — Базисная разность между текущей ценой инвестиционного актива и его фьючерсной ценой (ценой будущего периода). [ОАО РАО "ЕЭС России" СТО 17330282.27.010.001 2008] базис Разность между текущей (своп) ценой инвестиционного актива (как и… … Справочник технического переводчика
Базис — от греч. ba sis А. Основа, фундамент, база. Б. Надбавка или скидка к биржевой котировке. Является предметом торга, зависит от качества товара, условий поставки, сроков платежей и других факторов. Б. бывает увеличивающийся и уменьшающийся. Словарь … Словарь бизнес-терминов
БАЗИС — в геодезии линия на местности, измеряемая с высокой точностью и служащая для определения длин сторон геодезической сети в триангуляции … Большой Энциклопедический словарь
БАЗИС — БАЗИС, а, муж. 1. То же, что база (в 1 и 2 знач.). 2. В материалистическом социологическом учении: совокупность исторически сложившихся производственных отношений, лежащих в основе надстройки (в 3 знач.) данного общества. | прил. базисный, ая, ое … Толковый словарь Ожегова
БАЗИС — разбитая и тщательно промеренная на местности линия, служащая основой для дальнейших измерений. При съемках Б. прочно закрепляется столбами, рельсами или бетонными массивами с тем, чтобы при повторных измерениях (напр. при разбивке… … Технический железнодорожный словарь
Базис - это... Что такое Базис?
основная линия в сети геодезических треугольников, измеряемых для топографической съемки или для определения фигуры земли. Вся триангуляция дает только отношения длин сторон сети одной к другой или к какой-нибудь основной линии. Должно измерить со всей возможной точностью какую-нибудь определенную длину в сети, чтобы перевести все найденные величины из относительных в абсолютные. Ввиду того, что линейные измерения представляют громадные трудности в сравнении с измерениями углов, составляющими сущность триангуляции, базис в тригонометрической сети бывает всегда весьма мал в сравнении со всей длиной сети. Зато при измерении его принимаются всевозможные меры, чтобы точность измерения базиса компенсировала его небольшие размеры. Базисы в различных случаях бывают чрезвычайно различной длины. В топографической съемке они гораздо короче, чем в точных геодезических измерениях, где базисы обыкновенно имеют несколько верст длины. Шверд первый предложил измерять и в геодезических триангуляциях большой точности только короткие базисы и показал на примере Б. в Шпейере, что этим способом можно достигнуть столь же большой точности, как и при измерении сравнительно длинных Б. Именно, базис Шверда имел всего 441 туаза длины, но зато он измерялся несколько раз. Само измерение производится посредством т. н. базисного прибора, сущность которого составляет жезл, определенной длины, например в 2 туаза, который устанавливается на особых подставках на земле. Наблюдается температура жезла, наклон его к горизонту, определяется посредством особого постоянного сигнала положение начальной точки Б., и за одним жезлом приставляется следующий, причем точно определяется контакт обоих жезлов, и таким образом шаг за шагом подвигается измерение Б. до конечной точки, положение которой также фиксируется навсегда постоянным сигналом. Таким образом позднейшие съемки могут примыкать к предыдущим при помощи постоянных сигналов, оставленных на концах базиса или в каких-нибудь иных точках сети.
Базис (кристаллограф.), т. е. основание — сокращенное название базопинакоида, плоскости сидящей на конце главной вертикальной оси. Базопинакоид, или базис, есть открытая форма, состоящая из двух параллельных плоскостей, перпендикулярных к вертикальной оси в сист. квадратной, гексагональной и ромбической наклонных к ней в сист. манометрической и асимметрической. При рассматривании кристаллов их ставят так, что плоскости базопинакоида имеют горизонтальное положение. Б. существует во всех кристаллографических системах, кроме правильной. Сидящие кристаллы, особенно призматические, столбчатые, часто прикреплены плоскостью Б. к стенкам жилы или гнезд, в которых сидят, или к соседним кристаллам и т. д. (См. Кристаллографические сист.).
Базис (петрографич.). Многие изверженные горные породы, каковы порфиры, базальты, андезиты и т. д., особенно же различные лавы, кроме кристаллических составных частей содержат еще более или менее значительное количество неиндивидуализированного кристаллизационного остатка в виде совершенно бесструктурного стекловидного вещества, носящего название вулканического стекла, или в виде чешуйчатого, волокнистого "микрофельзита". Эта аморфная составная часть основной массы порфировидных горных пород и носит в петрографии название Б.
Базис (значения) - это... Что такое Базис (значения)?
- Базис (значения)
-
Ба́зис:
- В математике:
- Базис и надстройка — элементы политэкономической системы.
- Базис ячейки — совокупность координат узлов, которые задают элементарную кристаллическую ячейку.
- БАЗИС — серия компактных многоканальных промышленных контроллеров.
- Многозначные термины
Wikimedia Foundation. 2010.
- Уаймен, Билл
- Солонин, Марк Семёнович
Смотреть что такое "Базис (значения)" в других словарях:
Базис — У этого термина существуют и другие значения, см. Базис (значения). Базис (др. греч. βασις, основа) множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде… … Википедия
БАЗИС (серия контроллеров) — У этого термина существуют и другие значения, см. Базис (значения) … Википедия
Контроллеры БАЗИС — БАЗИС серия компактных многоканальных промышленных контроллеров, предназначенных для построения систем противоаварийной защиты и сигнализации, дискретного управления технологическими процессами, автоматического регулирования в различных областях… … Википедия
Дуальный базис — Тензор объект линейной алгебры. Частными случаями тензоров являются скаляры, векторы и билинейные формы. Часто тензор представляют как многомерную таблицу (где d размерность векторного пространства, над которым задан тензор, а число… … Википедия
Собственные векторы, значения и пространства — Синим цветом обозначен собственный вектор. Он, в отличие от красного, при деформации(преобразовании) не изменил направление и длину, поэтому является собственным вектором, соответствующим … Википедия
Определение (объяснение значения) — Определение, дефиниция (от лат. definitio), указание или объяснение значения (смысла) термина и (или) объёма (содержания) выражаемого данным термином понятия; этот термин (понятие) называется определяемым (лат. definiendum, сокращенно Dfd), а… … Большая советская энциклопедия
Собственные значения — линейного преобразования или оператора А, числа λ, для которых существует ненулевой вектор х такой, что Ах = λх; вектор х называется собственным вектором (См. Собственные векторы). Так, С. з. дифференциального оператора L (y) с заданными… … Большая советская энциклопедия
База — База: В Викисловаре есть статья «база» База (хранилище) место для хранения товаров, например: «овощная база». Военная база … Википедия
Симплекс-метод — Не путать с «симплекс методом» методом оптимизации произвольной функции. См. Метод Нелдера Мида Симплекс метод алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в… … Википедия
Метод главных компонент — (англ. Principal component analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях,… … Википедия
это что такое? Базис в математике, философии, экономике, астрономии
Базис - это основа. Об этом знают все. Однако далеко не каждый человек догадывается, что понятие базиса применимо в самых разных сферах. Философия, экономика, математика и даже астрономия - это лишь малая часть тех дисциплин, в которых используется понятие базиса. О соотношении системы и основной категории будет рассказано в нашей статье.
Базис и надстройка
В философии базис - это совокупность отношений производственного характера, которые могут существовать в общественной сфере. Такие отношения представляют собой объективное содержание всего социума. Это первичная, материальная часть, на основе которой формируются все прочие связи и элементы.
С понятием базиса тесно связана надстройка. Это совокупность социальных взглядов, идей, воззрений и теорий. Надстройка представляет собой систему идеологических отношений.
Базис - это первичное, надстройка - вторичное. На базе объективной и материальной системы возрастают духовные, идеологические отношения. Есть также ненадстроечные элементы, представляющие собой группы классов или семей.
Соотношение базиса и надстройки
Базис - это элемент, определяющий надстройку. Это главное правило исторического процесса по Марксу. В зависимости от материальной основы государства формируются типы социальной надстройки: философские, нравственные, правовые, идеологические и прочие связи. Природа государства тесно связана с базисом.

Переворот базиса всегда ведет к перекраиванию надстройки. При этом важно понимать, что каждой объективной основе соответствует своя надстроечная система: капиталистическому обществу - одна, феодальному - другая, социалистическому - третья и т.д. Иногда надстройка может опережать базис. Это может выражаться в принятии новаторских законов, издании прогрессивных актов и т.д. Такая тенденция свидетельствует о прогрессе в государстве. Это не прощание с действительностью, а напротив, приближение к ней. Марксисты объясняют такое явление не предвидением сознания, а реальным отражением будущей материальной основы.
Процесс создания материальных благ
Надстройка и базис - это основные категории в теории исторического материализма. Возникают они в строго установленном порядке. Для примера можно взять знаменитую пирамиду потребностей Абрхама Маслоу, где важнейшими нуждами были пища, отдых и безопасность, а лишь потом любовь, альтруизм и благородство. У неудовлетворенного человека процесс удовлетворения других людей далеко не в приоритете. Такого же мнения придерживались и марксисты.

Общество, равно как и человек, обладает приоритетными и второстепенными потребностями. Вначале формируется базис - материальная основа человечества. Это безопасность, наличие жилья и пищи - все то, что составляет объективный минимум. Лишь после появляется религия, творчество, политика, искусство - так называемые нематериальные блага.
Немарксистские концепции базиса
В философии базис - это понятие, толкование которому дают самые разные школы. Однако отцом-основателем знаменитой категории стал Карл Маркс. Его видение базиса и надстройки мы уже разобрали выше. Теперь же стоит обратить внимание на другие варианты толкования.
Даниел Белл делил общество на три типа, для каждого из которых характерны свои базисы и надстройки. Первый тип социума, доиндустриальный, базируется на добывающих формах хозяйства. Индустриальное общество определяется фабричным производством и массовыми технологиями. Постиндустриальное общество развивается в сфере услуг. Основной его целью является извлечение прибыли. Надстройка у каждого общества разная.

По Иноземцеву общество делится на доэкономическое, экономическое и постэкономическое. Надстройка у первой формы социума слишком проста: это приоритет коллективных отношений и борьба за выживание. Свое развитие вторичная сфера получает с появление частной собственности и, как следствие, эксплуатации. Вершиной надстройки является творчество, характерное для постиндустриального общества.
Экономическая концепция
Базис в экономике - это понятие, ничем не отличимое от философского. Правда, смотреть на него нужно чуть под другим углом. Важную роль здесь играет понятие производственных сил. Так называют людей - элементов общества, обладающих орудиями производства и способных использовать их по назначению. Производственные силы вступают в производственные отношения. Люди создают блага, устанавливают друг с другом контакты и модернизируют свою деятельность.

Связи и отношения как раз являются базисом. От способа производства зависит идеология, взгляды и политические институты - элементы, которые будут влиять на развитие базиса.
Таким образом, экономический базис - это совокупность производственных отношений между людьми. Он детерминирует все стороны жизни социума, определяет его структуру. Важное дополнение: базис формируется не по произволу, а согласно общественным и экономическим законам. Люди подчиняются требованиям, которые сами себе создают, и условия для которых готовит внешняя среда.
Базис в математике
В математике базис - это строго упорядоченный набор векторов в пространстве. Набор может быть конечным или бесконечным. Существуют разные комбинации базиса. Зависят они от порядка построения имеющихся векторов.
"Базис" - это древнегреческий термин, введенный античным математиком Евклидом. Мыслитель понимал базис как горизонтальное основание пространственной или плоской фигуры. Современный смысл понятию придал немецкий математик Юлиус Дедекинд. В статье 1885 года появились первые заметки о системе координат на плоскости или в трехмерном пространстве.
Базис состоит из векторов, каждый из которых направлен вдоль своей координатной оси. Если углы между векторами равны 90 градусов, то такой базис именуется ортогональным. Если все векторы конечны и имеют одинаковую длину, то речь пойдет о нормированном базисе. Бывают также зеркально отраженные совокупности векторов, которые невозможно соединить. Помимо трехмерных, бывают четырехмерные, пятимерные и прочие виды математических базисов.
Базис в астрономии
Базис - это расстояние до тела. Так трактуют знаменитое понятие астрономы. Для определения базиса используется метод параллакса: измеряется расстояние до доступной точки. Также берется угол, под которым на горизонте необходимого тела был бы виден базис. Такой угол называется экваториальным параллаксом. Используя угломерный геометрический способ, можно с точностью определить расстояние (базис) до необходимых объектов.
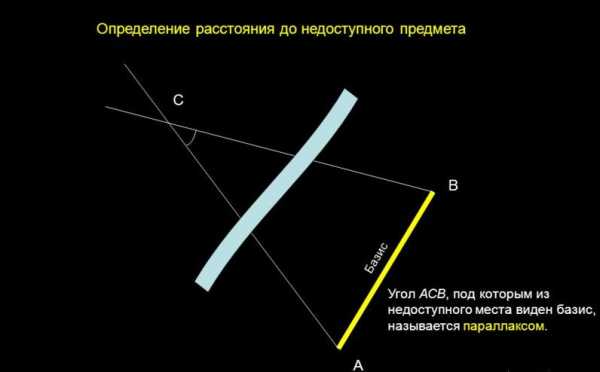
Можно привести пример. Зная расстояние от Земли до Солнца, мы можем вычесть среднее расстояние всех планет от главного светила. За базис берется радиус Земли. Из разных точек, в которых расположены обсерватории, определяется наблюдаемый объект. Два вектора наблюдения из разных точек пересекаются, находится угол пересечения. Вычислив угол, можно определить параллакс, а в дальнейшем и расстояние до нужного объекта.
БАЗИС - это... Что такое БАЗИС?
БАЗИС — разница (премия или скидка) между ценой наличного товара и то вара с поставкой на срок, между ценой по сделкам с реальным товаром и биржевыми котировками. Обычно указывается в пунктах вверх или вниз отбиржевой котировки. Используется при… … Финансовый словарь
БАЗИС — 1) основание колонны; 2) вообще основание, подножие, постамент; 3) операционный базис часть местности в тылу действующей армии, служащая для неё опорой; в ней бывают собраны резервы, провиант, припасы и т. д.; 4) точно измеряемая прямая линия для … Словарь иностранных слов русского языка
базис — См … Словарь синонимов
БАЗИС — (греч. basis основание) основа, основание; опора, фундамент, база. Напр., базис колонны, базис программы … Большой Энциклопедический словарь
БАЗИС — БАЗИС, базиса, муж. (греч. basis основание, пьедестал). 1. То же, что база в 1 знач. (архит.). Базис колонны. 2. только ед. То же, что база во 2 знач. (книжн.). Подвести базу подо что н: (твердо обосновать что нибудь, подтвердить что нибудь… … Толковый словарь Ушакова
БАЗИС — (греч. basis) надбавка к биржевой котировке или скидка с нее, являющаяся предметом торга. Она зависит от сорта и качества товара, условий поставки, платежей и др. факторов. Увеличивающийся базис указывается в пунктах вверх от биржевой котировки,… … Экономический словарь
базис — Базисная разность между текущей ценой инвестиционного актива и его фьючерсной ценой (ценой будущего периода). [ОАО РАО "ЕЭС России" СТО 17330282.27.010.001 2008] базис Разность между текущей (своп) ценой инвестиционного актива (как и… … Справочник технического переводчика
Базис — от греч. ba sis А. Основа, фундамент, база. Б. Надбавка или скидка к биржевой котировке. Является предметом торга, зависит от качества товара, условий поставки, сроков платежей и других факторов. Б. бывает увеличивающийся и уменьшающийся. Словарь … Словарь бизнес-терминов
БАЗИС — в геодезии линия на местности, измеряемая с высокой точностью и служащая для определения длин сторон геодезической сети в триангуляции … Большой Энциклопедический словарь
БАЗИС — разбитая и тщательно промеренная на местности линия, служащая основой для дальнейших измерений. При съемках Б. прочно закрепляется столбами, рельсами или бетонными массивами с тем, чтобы при повторных измерениях (напр. при разбивке… … Технический железнодорожный словарь
БАЗИС - это... Что такое БАЗИС?
БАЗИС — 1) основание колонны; 2) вообще основание, подножие, постамент; 3) операционный базис часть местности в тылу действующей армии, служащая для неё опорой; в ней бывают собраны резервы, провиант, припасы и т. д.; 4) точно измеряемая прямая линия для … Словарь иностранных слов русского языка
базис — См … Словарь синонимов
БАЗИС — (греч. basis основание) основа, основание; опора, фундамент, база. Напр., базис колонны, базис программы … Большой Энциклопедический словарь
БАЗИС — БАЗИС, базиса, муж. (греч. basis основание, пьедестал). 1. То же, что база в 1 знач. (архит.). Базис колонны. 2. только ед. То же, что база во 2 знач. (книжн.). Подвести базу подо что н: (твердо обосновать что нибудь, подтвердить что нибудь… … Толковый словарь Ушакова
БАЗИС — (греч. basis) надбавка к биржевой котировке или скидка с нее, являющаяся предметом торга. Она зависит от сорта и качества товара, условий поставки, платежей и др. факторов. Увеличивающийся базис указывается в пунктах вверх от биржевой котировки,… … Экономический словарь
базис — Базисная разность между текущей ценой инвестиционного актива и его фьючерсной ценой (ценой будущего периода). [ОАО РАО "ЕЭС России" СТО 17330282.27.010.001 2008] базис Разность между текущей (своп) ценой инвестиционного актива (как и… … Справочник технического переводчика
Базис — от греч. ba sis А. Основа, фундамент, база. Б. Надбавка или скидка к биржевой котировке. Является предметом торга, зависит от качества товара, условий поставки, сроков платежей и других факторов. Б. бывает увеличивающийся и уменьшающийся. Словарь … Словарь бизнес-терминов
БАЗИС — в геодезии линия на местности, измеряемая с высокой точностью и служащая для определения длин сторон геодезической сети в триангуляции … Большой Энциклопедический словарь
БАЗИС — БАЗИС, а, муж. 1. То же, что база (в 1 и 2 знач.). 2. В материалистическом социологическом учении: совокупность исторически сложившихся производственных отношений, лежащих в основе надстройки (в 3 знач.) данного общества. | прил. базисный, ая, ое … Толковый словарь Ожегова
БАЗИС — разбитая и тщательно промеренная на местности линия, служащая основой для дальнейших измерений. При съемках Б. прочно закрепляется столбами, рельсами или бетонными массивами с тем, чтобы при повторных измерениях (напр. при разбивке… … Технический железнодорожный словарь
БАЗИС - это... Что такое БАЗИС?
БАЗИС — разница (премия или скидка) между ценой наличного товара и то вара с поставкой на срок, между ценой по сделкам с реальным товаром и биржевыми котировками. Обычно указывается в пунктах вверх или вниз отбиржевой котировки. Используется при… … Финансовый словарь
БАЗИС — 1) основание колонны; 2) вообще основание, подножие, постамент; 3) операционный базис часть местности в тылу действующей армии, служащая для неё опорой; в ней бывают собраны резервы, провиант, припасы и т. д.; 4) точно измеряемая прямая линия для … Словарь иностранных слов русского языка
базис — См … Словарь синонимов
БАЗИС — (греч. basis основание) основа, основание; опора, фундамент, база. Напр., базис колонны, базис программы … Большой Энциклопедический словарь
БАЗИС — (греч. basis) надбавка к биржевой котировке или скидка с нее, являющаяся предметом торга. Она зависит от сорта и качества товара, условий поставки, платежей и др. факторов. Увеличивающийся базис указывается в пунктах вверх от биржевой котировки,… … Экономический словарь
базис — Базисная разность между текущей ценой инвестиционного актива и его фьючерсной ценой (ценой будущего периода). [ОАО РАО "ЕЭС России" СТО 17330282.27.010.001 2008] базис Разность между текущей (своп) ценой инвестиционного актива (как и… … Справочник технического переводчика
Базис — от греч. ba sis А. Основа, фундамент, база. Б. Надбавка или скидка к биржевой котировке. Является предметом торга, зависит от качества товара, условий поставки, сроков платежей и других факторов. Б. бывает увеличивающийся и уменьшающийся. Словарь … Словарь бизнес-терминов
БАЗИС — в геодезии линия на местности, измеряемая с высокой точностью и служащая для определения длин сторон геодезической сети в триангуляции … Большой Энциклопедический словарь
БАЗИС — БАЗИС, а, муж. 1. То же, что база (в 1 и 2 знач.). 2. В материалистическом социологическом учении: совокупность исторически сложившихся производственных отношений, лежащих в основе надстройки (в 3 знач.) данного общества. | прил. базисный, ая, ое … Толковый словарь Ожегова
БАЗИС — разбитая и тщательно промеренная на местности линия, служащая основой для дальнейших измерений. При съемках Б. прочно закрепляется столбами, рельсами или бетонными массивами с тем, чтобы при повторных измерениях (напр. при разбивке… … Технический железнодорожный словарь
Лекция 9. Базис векторного пространства
Лекции по алгебре и геометрии. Семестр 1.
Лекция 9. Базис векторного пространства.
Краткое содержание: система векторов, линейная комбинация системы векторов, коэффициенты линейной комбинации системы векторов, базис на прямой, плоскости и в пространстве, размерности векторных пространств на прямой, плоскости и в пространстве, разложение вектора по базису, координаты вектора относительно базиса, теорема о равенстве двух векторов, линейные операции с векторами в координатной форме записи, ортонормированная тройка векторов, правая и левая тройки векторов, ортонормированный базис, основная теорема векторной алгебры.
Глава 9. Базис векторного пространства и разложение вектора по базису.
п.1. Базис на прямой, на плоскости и в пространстве.
Определение. Любое конечное множество векторов называется системой векторов.
Определение. Выражение , где называется линейной комбинацией системы векторов , а числа называются коэффициентами этой линейной комбинации.
Пусть L, Р и S – прямая, плоскость и пространство точек соответственно и . Тогда – векторные пространства векторов как направленных отрезков на прямой L, на плоскости Р и в пространстве S соответственно.
Определение. Базисом векторного пространства 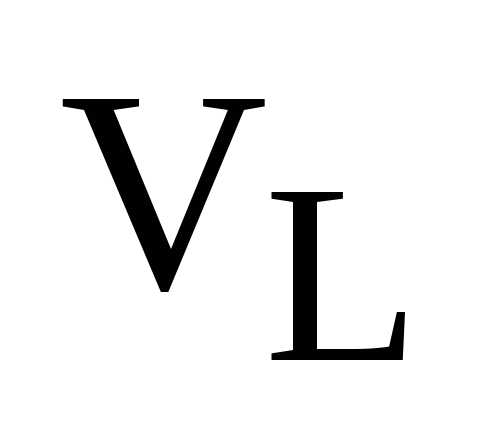 называется любой ненулевой вектор
называется любой ненулевой вектор 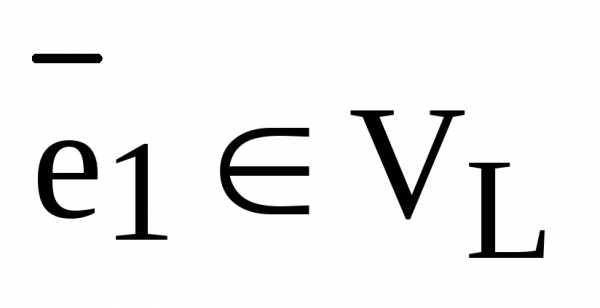 , т.е. любой ненулевой вектор коллинеарный прямой L:
, т.е. любой ненулевой вектор коллинеарный прямой L: 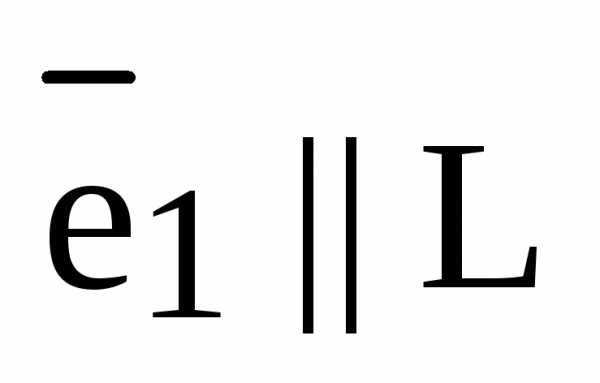 и
и 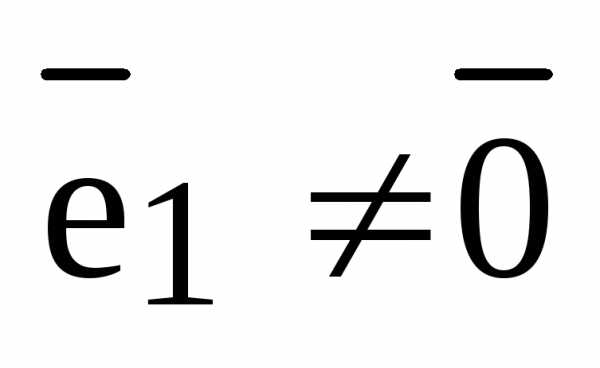 .
.
Обозначение базиса  :
: 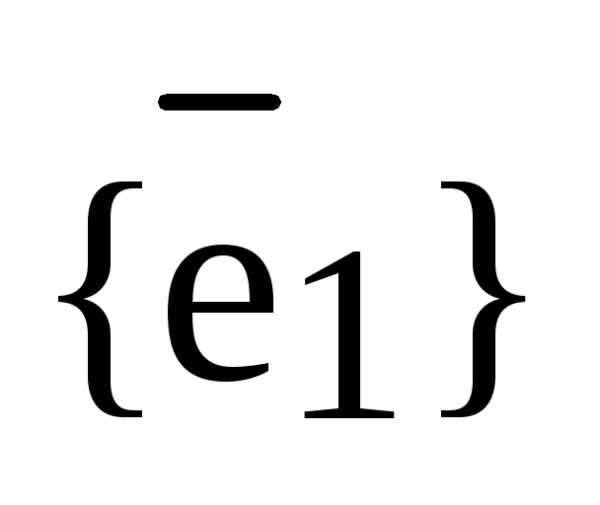 – базис
– базис  .
.
Определение. Базисом векторного пространства  называется любая упорядоченная пара неколлинеарных векторов пространства
называется любая упорядоченная пара неколлинеарных векторов пространства  .
.
рис.1.
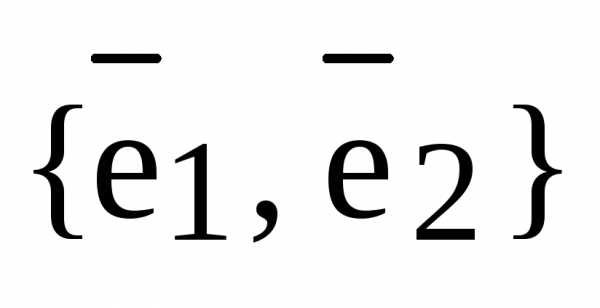 , где
, где  ,
,  – базис
– базис  .
.
Определение. Базисом векторного пространства  называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства
называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства  .
.
рис.2.
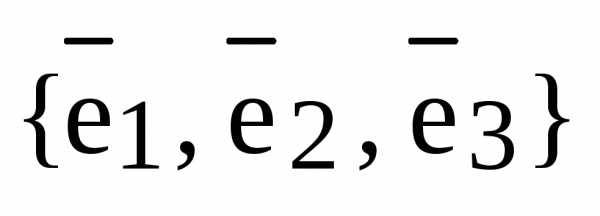 – базис
– базис  .
.
Замечание. Базис векторного пространства не может содержать нулевого вектора: в пространстве 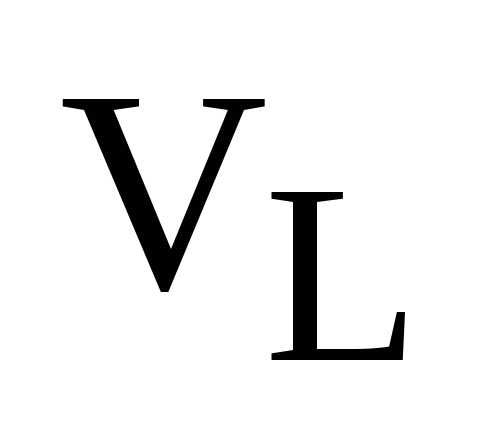 по определению, в пространстве
по определению, в пространстве  два вектора будут коллинеарные, если хотя бы один из них нулевой, в пространстве
два вектора будут коллинеарные, если хотя бы один из них нулевой, в пространстве  три вектора будут компланарные, т.е будут лежать в одной плоскости, если хотя бы один из трех векторов будет нулевой.
три вектора будут компланарные, т.е будут лежать в одной плоскости, если хотя бы один из трех векторов будет нулевой.
п.2. Разложение вектора по базису.
Определение. Пусть  – произвольный вектор, – произвольная система векторов. Если выполняется равенство
– произвольный вектор, – произвольная система векторов. Если выполняется равенство
, (1)
то говорят, что вектор  представлен в виде линейной комбинации данной системы векторов. Если данная система векторов является базисом векторного пространства, то равенство (1) называется разложением вектора
представлен в виде линейной комбинации данной системы векторов. Если данная система векторов является базисом векторного пространства, то равенство (1) называется разложением вектора  по базису . Коэффициенты линейной комбинации называются в этом случае координатами вектора
по базису . Коэффициенты линейной комбинации называются в этом случае координатами вектора  относительно базиса .
относительно базиса .
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Доказательство. 1) Пусть L произвольная прямая (или ось) и 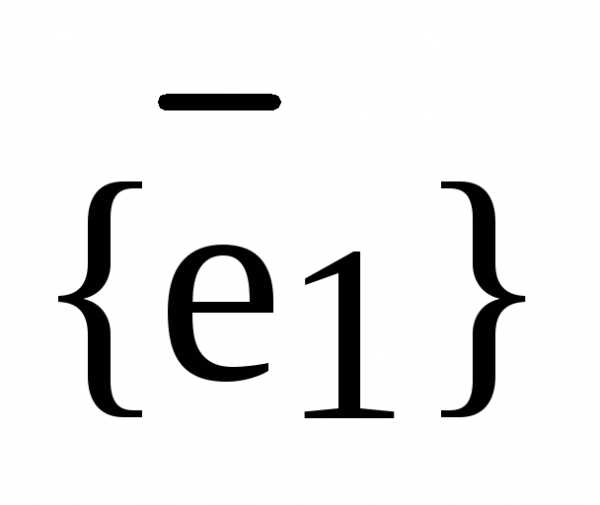 – базис
– базис 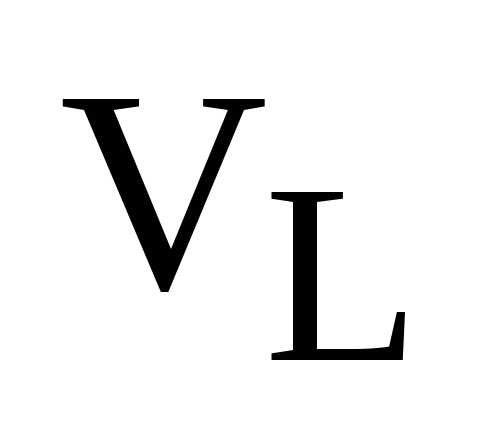 . Возьмем произвольный вектор
. Возьмем произвольный вектор 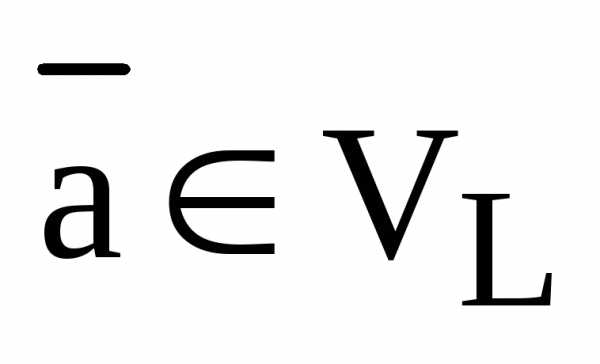 . Так как оба вектора
. Так как оба вектора 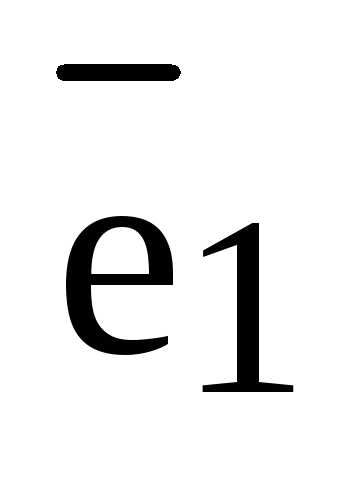 и
и  коллинеарные одной и той же прямой L, то
коллинеарные одной и той же прямой L, то 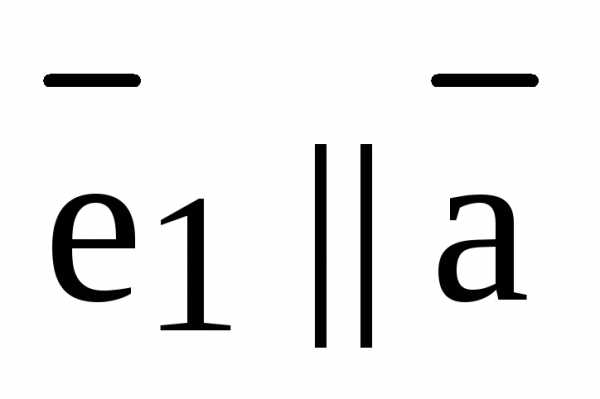 . Воспользуемся теоремой о коллинеарности двух векторов. Так как
. Воспользуемся теоремой о коллинеарности двух векторов. Так как 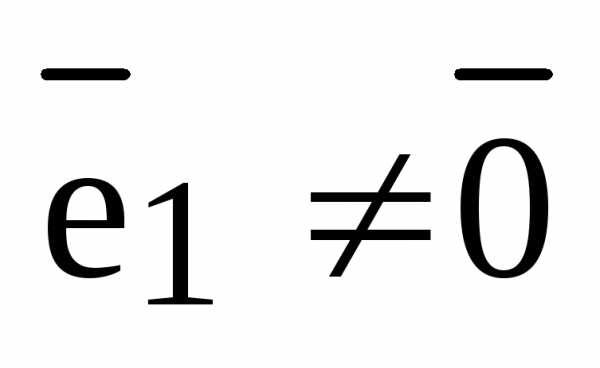 , то найдется (существует) такое число
, то найдется (существует) такое число  , что
, что 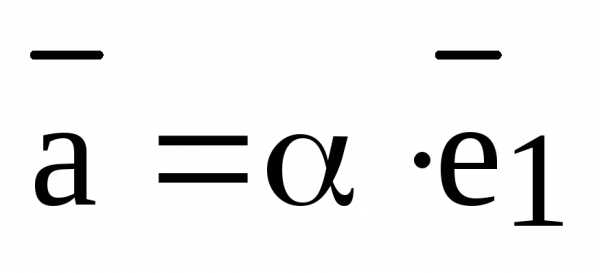 и тем самым мы получили разложение вектора
и тем самым мы получили разложение вектора  по базису
по базису 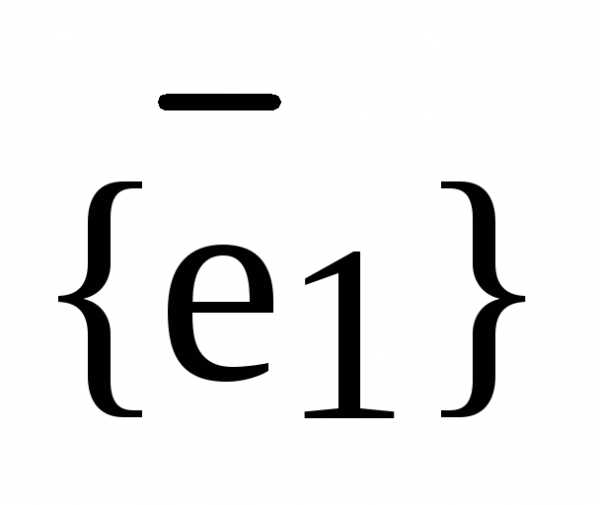 векторного пространства
векторного пространства 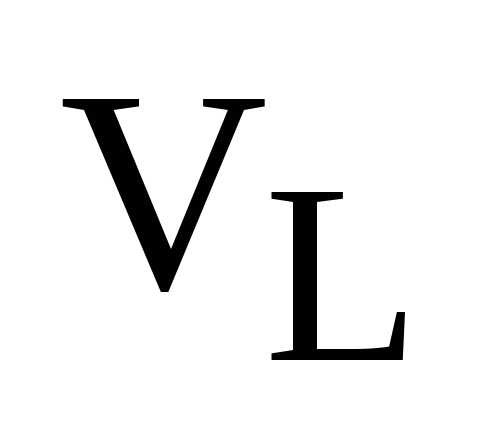 .
.
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису
по базису 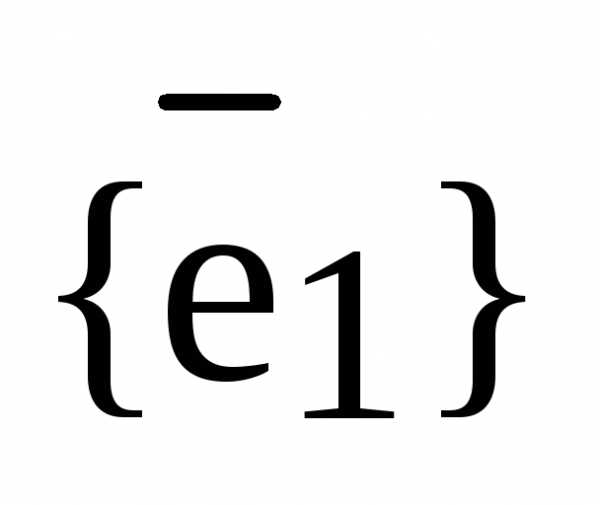 векторного пространства
векторного пространства  :
:
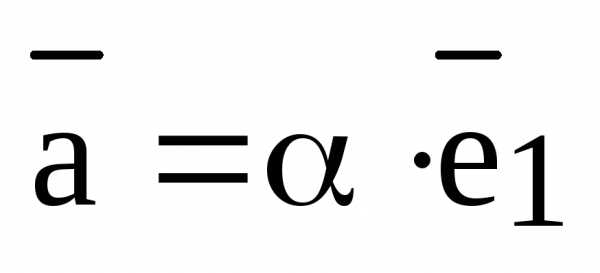 и
и 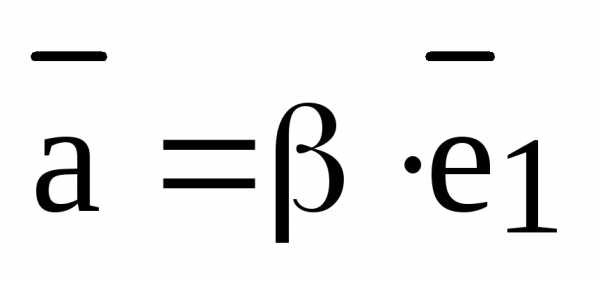 , где
, где  . Тогда и используя закон дистрибутивности, получаем:
. Тогда и используя закон дистрибутивности, получаем:
.
Так как 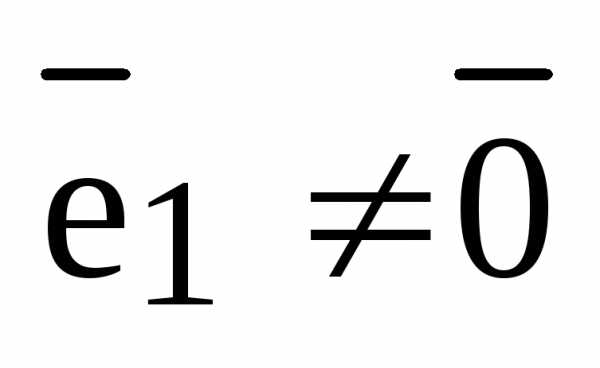 , то из последнего равенства следует, что
, то из последнего равенства следует, что 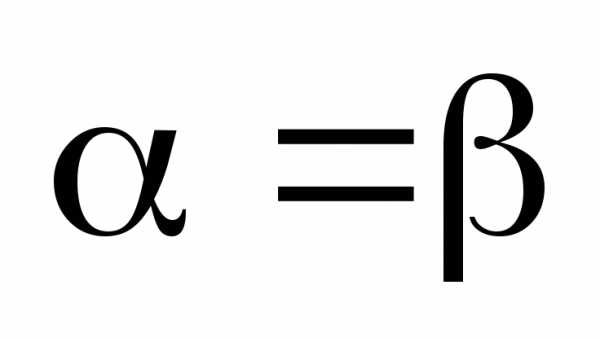 , ч.т.д.
, ч.т.д.
2) Пусть теперь Р произвольная плоскость и 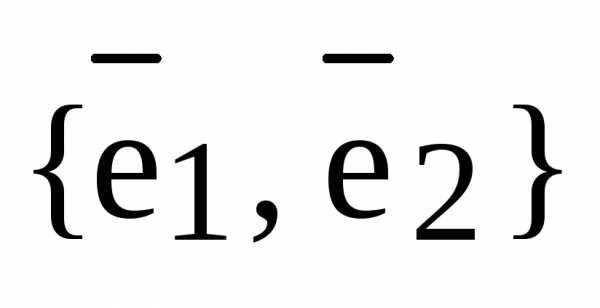 – базис
– базис  . Пусть
. Пусть  произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую
произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую  , на которой лежит вектор
, на которой лежит вектор 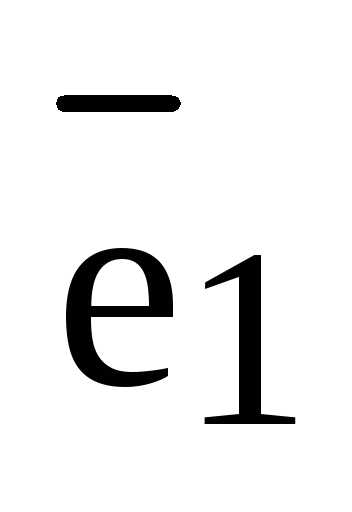 , прямую
, прямую 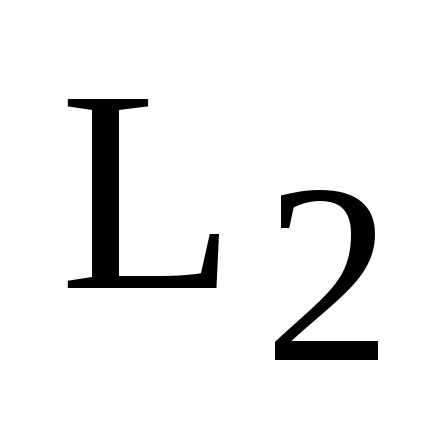 , на которой лежит вектор
, на которой лежит вектор 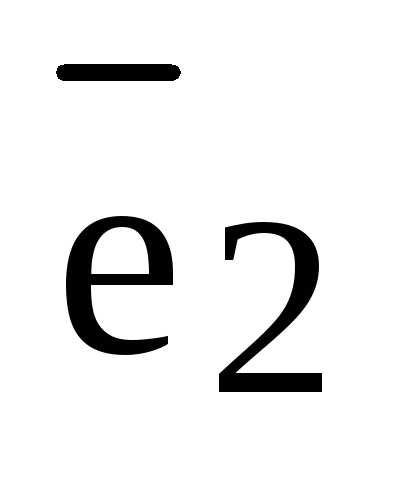 . Через конец вектора
. Через конец вектора  проведем прямую параллельную вектору
проведем прямую параллельную вектору 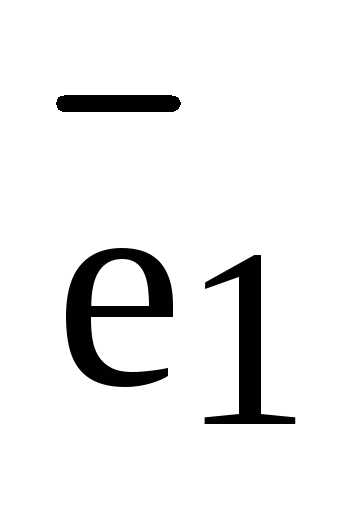 и прямую параллельную вектору
и прямую параллельную вектору 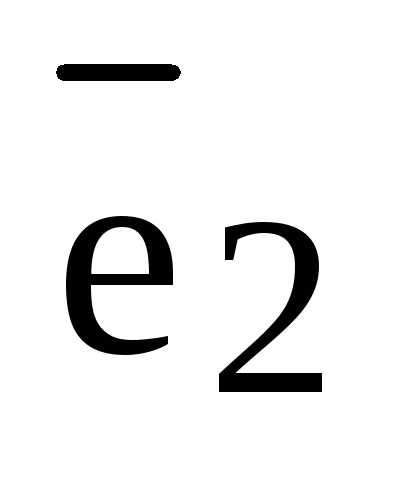 . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма
. Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма 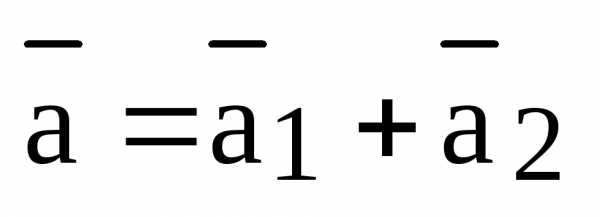 , и
, и  ,
,  ,
, 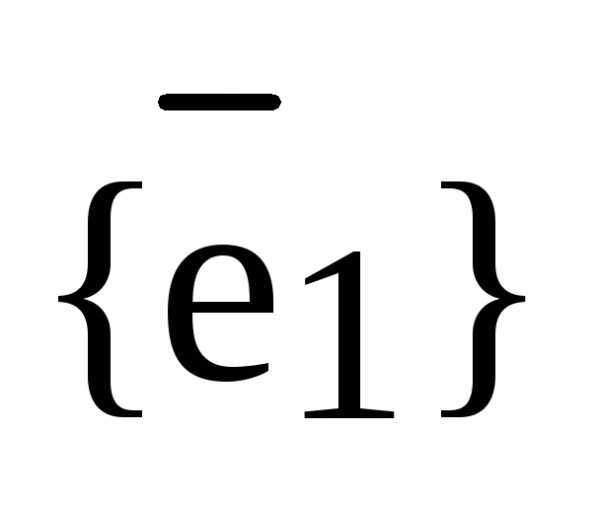 – базис
– базис 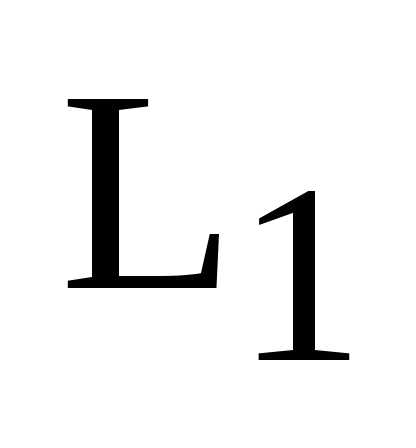 ,
, 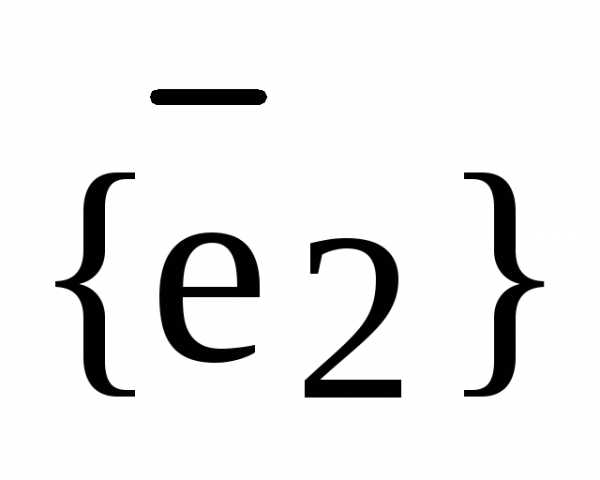 – базис
– базис 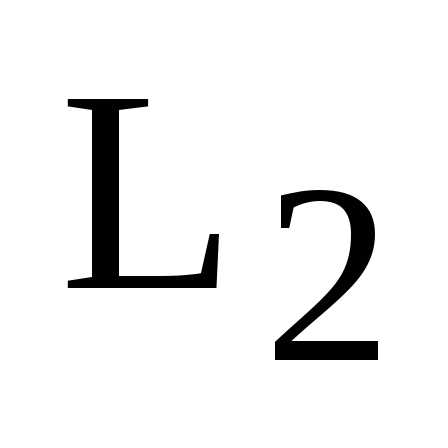 .
.
Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа , что
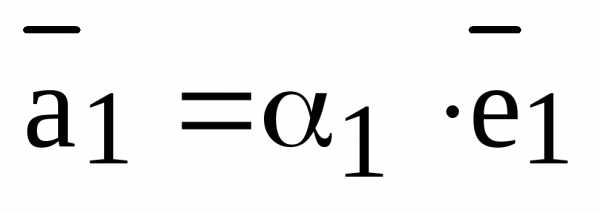 и
и 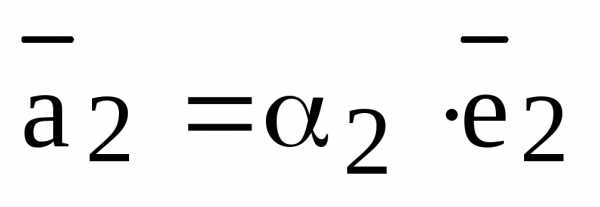 . Отсюда получаем:
. Отсюда получаем:
и возможность разложения по базису доказана.
рис.3.
Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора  по базису
по базису 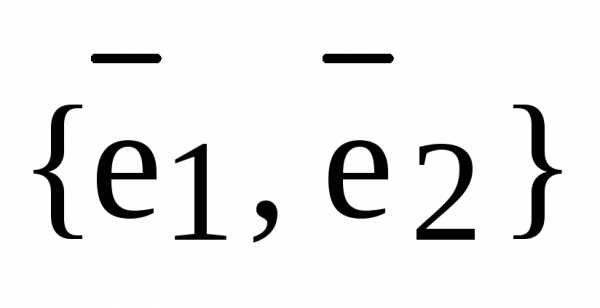 векторного пространства
векторного пространства  : и . Получаем равенство
: и . Получаем равенство
, откуда следует . Если , то , а т.к. 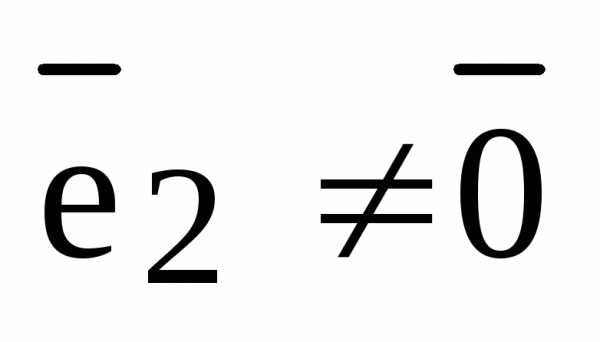 , то и коэффициенты разложения равны:
, то и коэффициенты разложения равны: 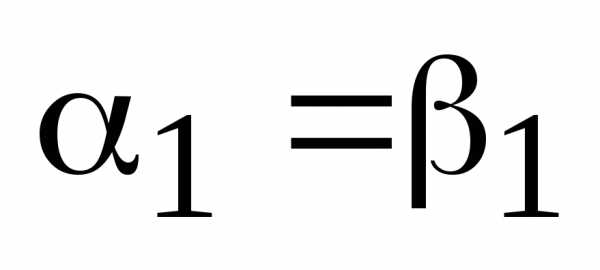 ,
, 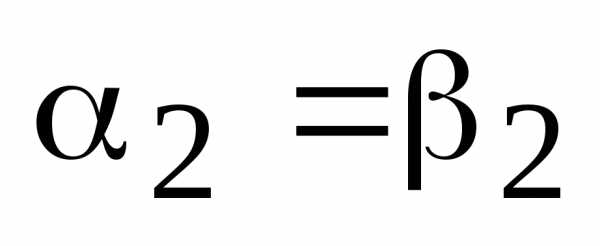 . Пусть теперь . Тогда , где
. Пусть теперь . Тогда , где 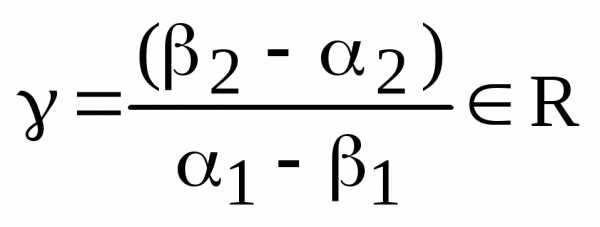 . По теореме о коллинеарности двух векторов отсюда следует, что
. По теореме о коллинеарности двух векторов отсюда следует, что  . Получили противоречие условию теоремы. Следовательно,
. Получили противоречие условию теоремы. Следовательно, 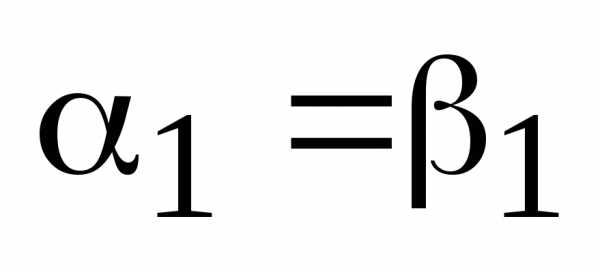 и
и 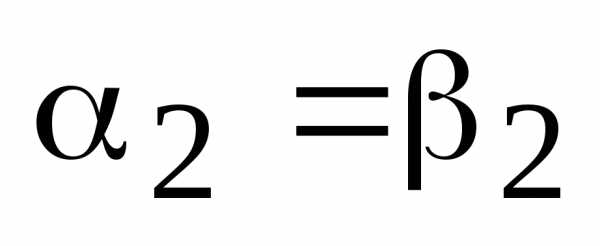 , ч.т.д.
, ч.т.д.
3) Пусть 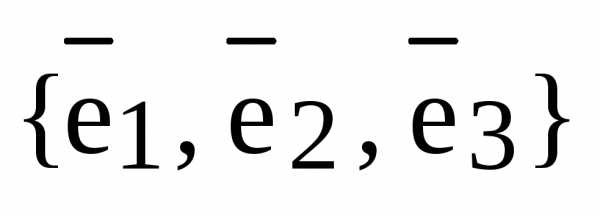 – базис
– базис  и пусть
и пусть 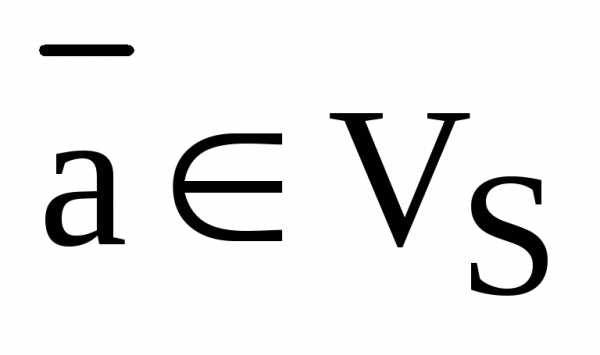 произвольный вектор. Проведем следующие построения.
произвольный вектор. Проведем следующие построения.
Отложим все три базисных вектора 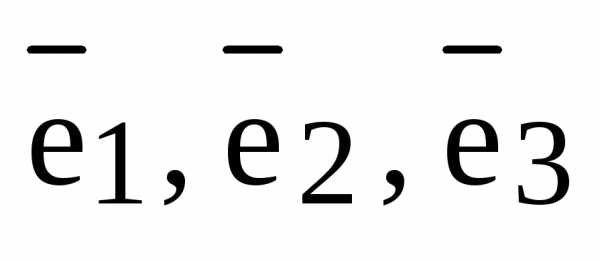 и вектор
и вектор  от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы
от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы 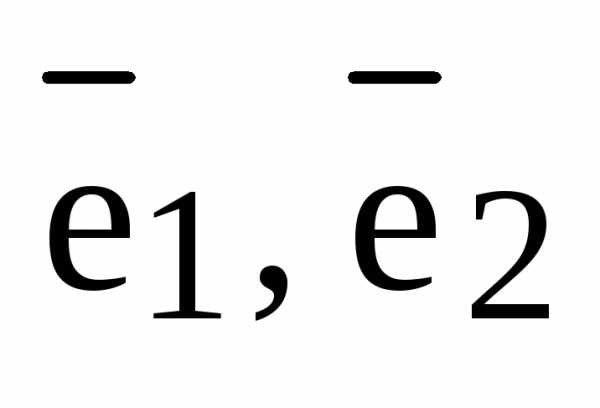 , плоскость
, плоскость 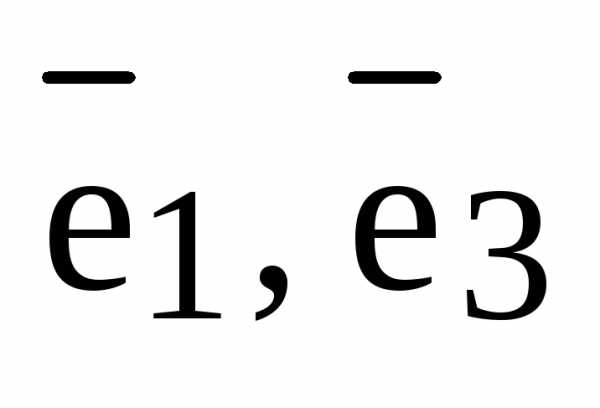 и плоскость
и плоскость 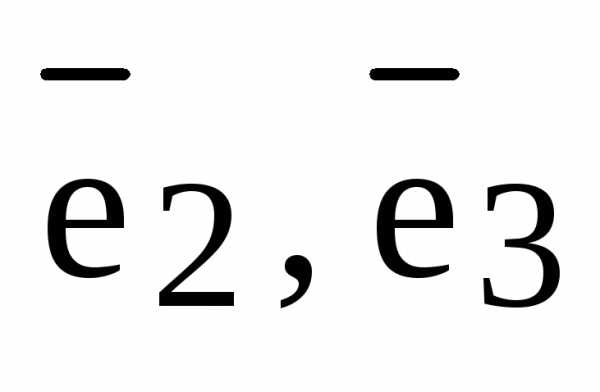 ; далее через конец вектора
; далее через конец вектора  проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:
проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:
рис.4.
По правилу сложения векторов получаем равенство:
. (1)
По построению . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число 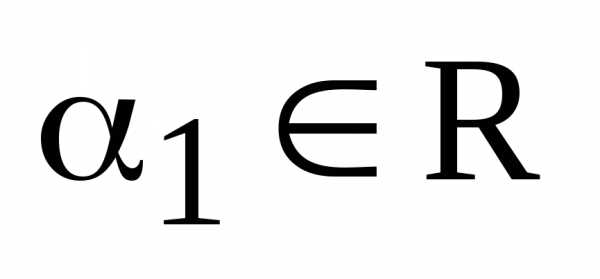 , такое что
, такое что 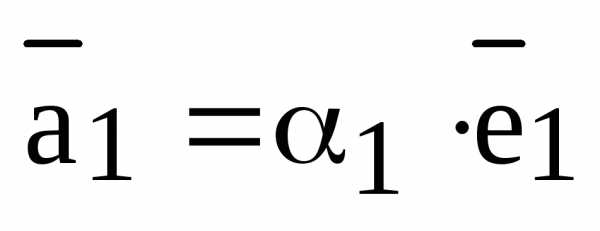 . Аналогично, и
. Аналогично, и 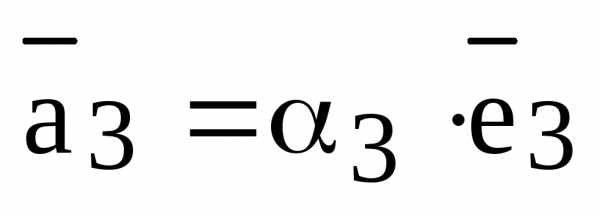 , где . Теперь, подставляя эти равенства в (1), получаем:
, где . Теперь, подставляя эти равенства в (1), получаем:
(2)
и возможность разложения по базису доказана.
Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису
по базису 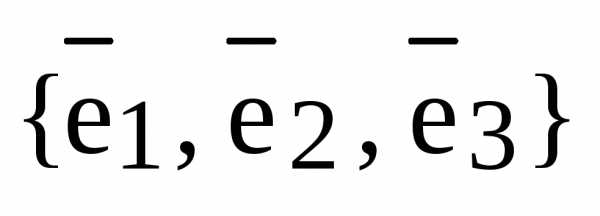 :
:
и . Тогда
. (3)
Заметим, что по условию векторы 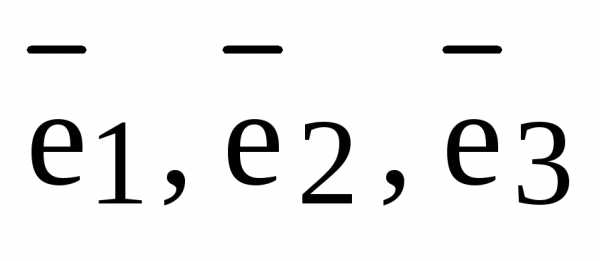 некомпланарные, следовательно, они попарно неколлинеарные.
некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая: или .
а) Пусть , тогда из равенства (3) следует:
. (4)
Из равенства (4) следует, что вектор  раскладывается по базису
раскладывается по базису  , т.е. вектор
, т.е. вектор  лежит в плоскости векторов
лежит в плоскости векторов 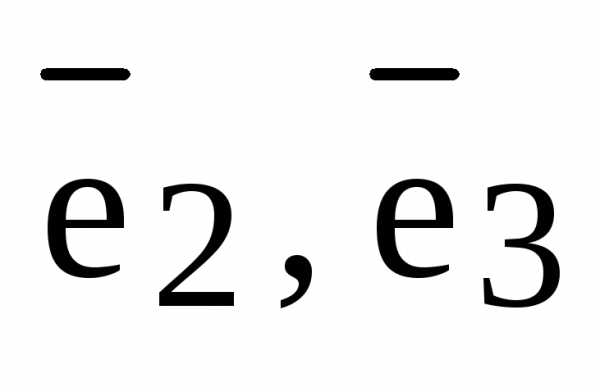 и, следовательно, векторы
и, следовательно, векторы  компланарные, что противоречит условию.
компланарные, что противоречит условию.
б) Остается случай , т.е.  . Тогда из равенства (3) получаем или
. Тогда из равенства (3) получаем или
. (5)
Так как  – базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что
– базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что 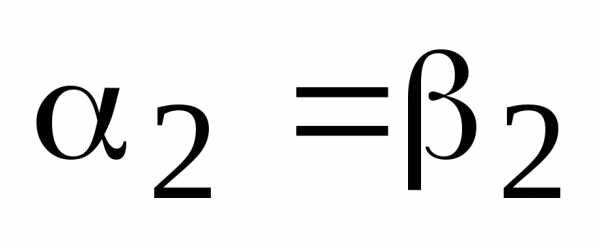 и
и 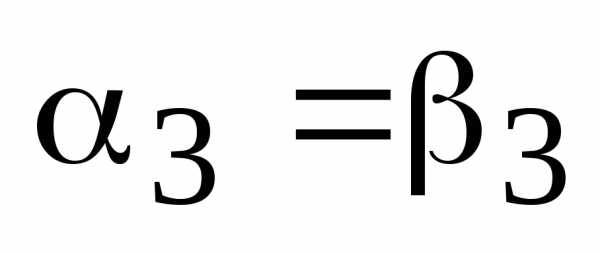 , ч.т.д.
, ч.т.д.
Теорема доказана.
Следствие.
1) Существует взаимно однозначное соответствие между множеством векторов векторного пространства  и множеством действительных чисел R.
и множеством действительных чисел R.
2) Существует взаимно однозначное соответствие между множеством векторов векторного пространства  и декартовым квадратом
и декартовым квадратом  множества действительных чисел R.
множества действительных чисел R.
3) Существует взаимно однозначное соответствие между множеством векторов векторного пространства  и декартовым кубом
и декартовым кубом  множества действительных чисел R.
множества действительных чисел R.
Доказательство. Докажем третье утверждение. Первые два доказываются аналогично.
Выберем и зафиксируем в пространстве  какой-нибудь базис
какой-нибудь базис 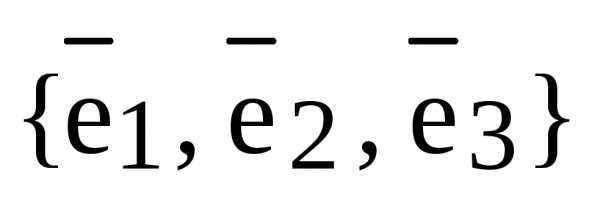 и устроим отображение
и устроим отображение 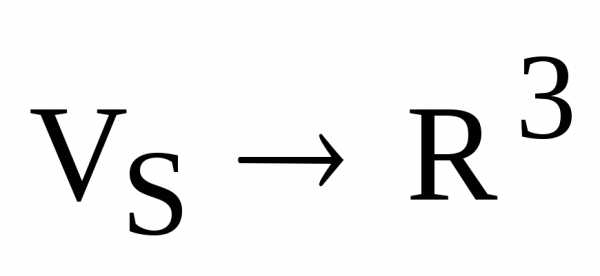 по следующему правилу:
по следующему правилу:
, (6)
т.е. каждому вектору поставим в соответствие упорядоченный набор его координат.
Так как при фиксированном базисе каждый вектор имеет единственный набор координат, то соответствие, задаваемое правилом (6) действительно является отображением.
Из доказательства теоремы следует, что различные векторы имеют различные координаты относительно одного и того же базиса, т.е. отображение (6) является инъекцией.
Пусть 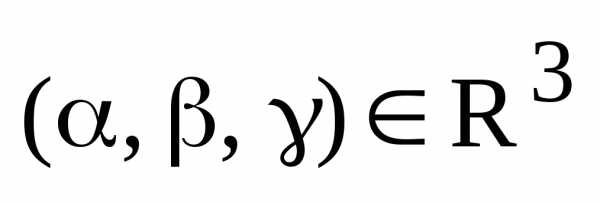 произвольный упорядоченный набор действительных чисел.
произвольный упорядоченный набор действительных чисел.
Рассмотрим вектор . Этот вектор по построению имеет координаты 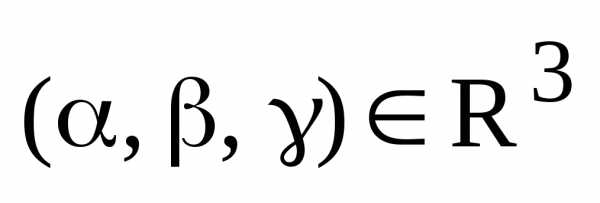 . Следовательно, отображение (6) является сюръекцией.
. Следовательно, отображение (6) является сюръекцией.
Отображение, которое одновременно инъективное и сюръективное является биективным, т.е. взаимно однозначным, ч.т.д.
Следствие доказано.
Теорема. (О равенстве двух векторов.)
Два вектора равны тогда и только тогда, когда равны их координаты относительно одного и того же базиса.
Доказательство сразу же вытекает из предыдущего следствия.
п.3. Размерность векторного пространства.
Определение. Число векторов в базисе векторного пространства называется его размерностью.
Обозначение: 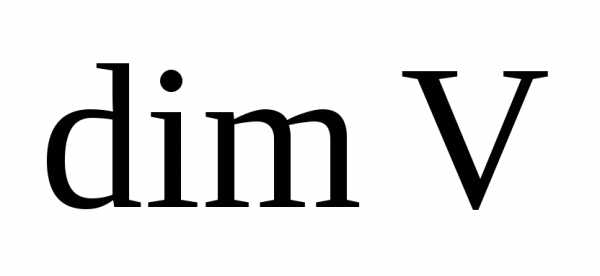 – размерность векторного пространства V.
– размерность векторного пространства V.
Таким образом, в соответствие с этим и предыдущими определениями, имеем:
1) 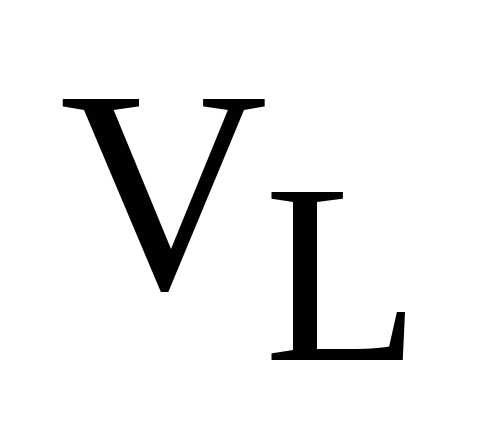 – векторное пространство векторов прямой L.
– векторное пространство векторов прямой L.
 – базис
– базис 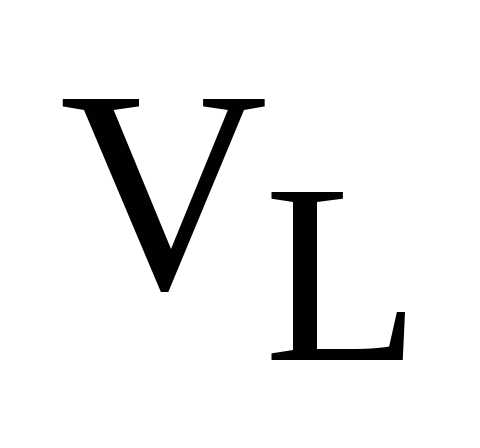 , ,
, , 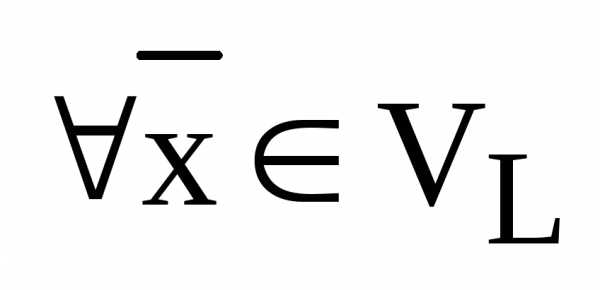 ,
, 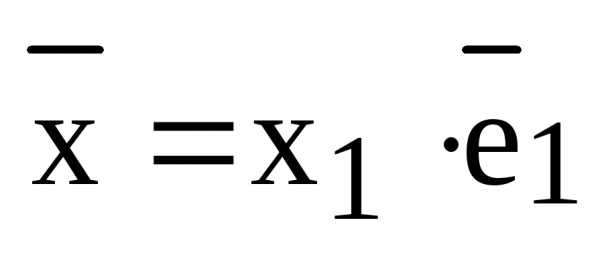 – разложение вектора
– разложение вектора 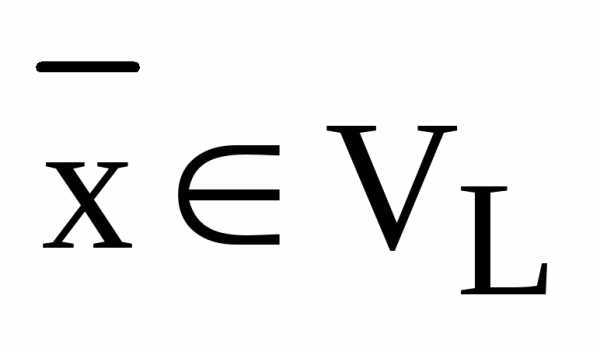 по базису
по базису 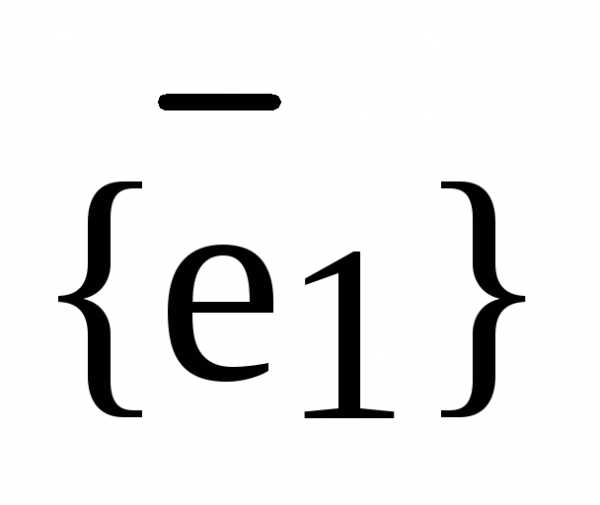 ,
, 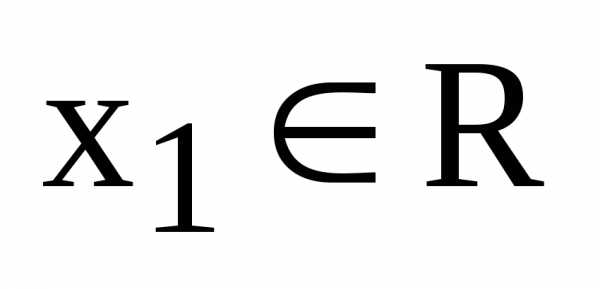 – координата вектора
– координата вектора 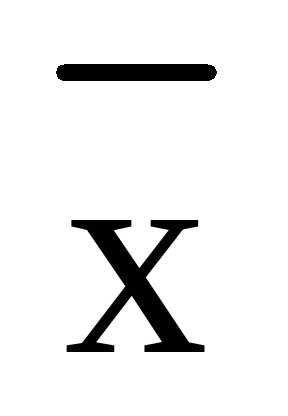 относительно базиса
относительно базиса 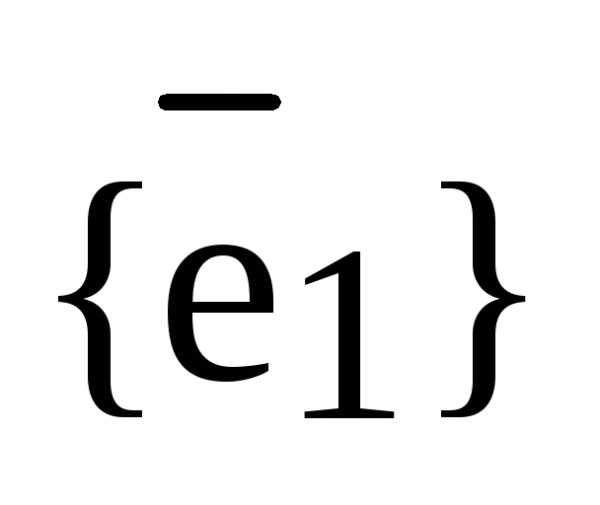 .
.
2)  – векторное пространство векторов плоскости Р.
– векторное пространство векторов плоскости Р.
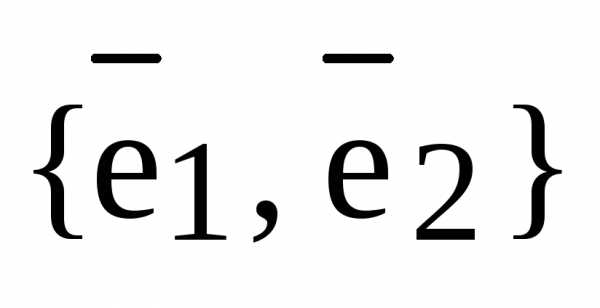 – базис
– базис  , ,
, ,  , – разложение вектора
, – разложение вектора  по базису , – координаты вектора
по базису , – координаты вектора 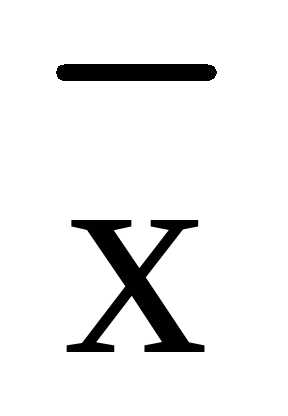 относительно базиса
относительно базиса  .
.
3)  – векторное пространство векторов в пространстве точек S.
– векторное пространство векторов в пространстве точек S.
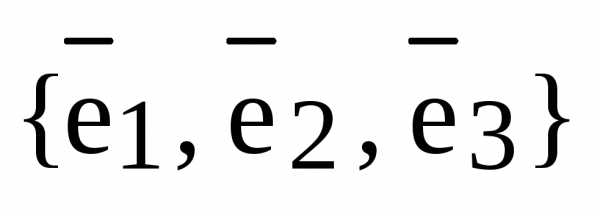 – базис
– базис  , ,
, , 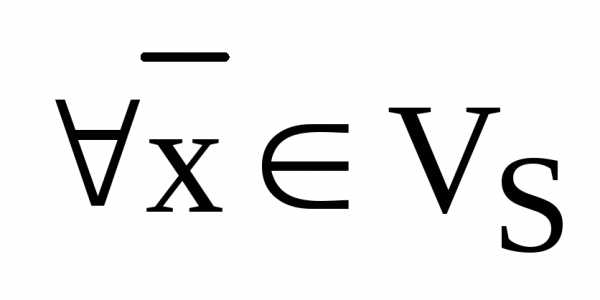 – разложение вектора
– разложение вектора 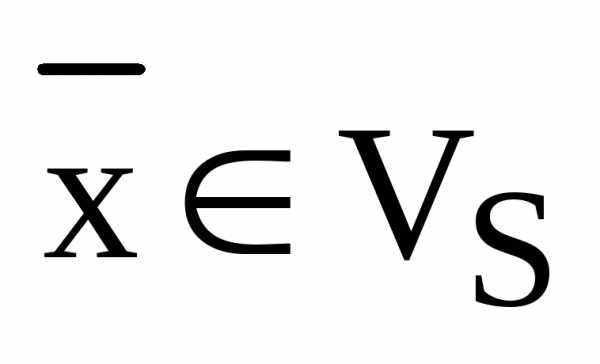 по базису
по базису  , – координаты вектора
, – координаты вектора 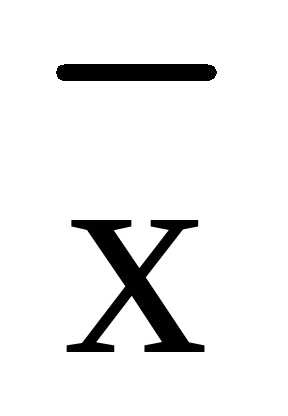 относительно базиса
относительно базиса 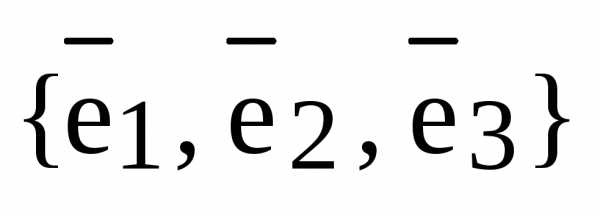 .
.
Замечание. Если , то и можно выбрать базис 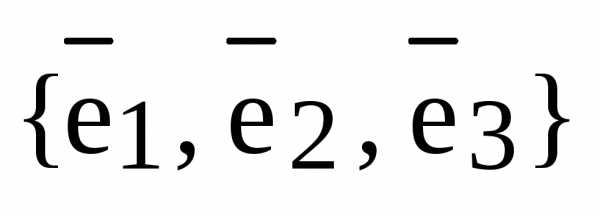 пространства
пространства  так, что
так, что 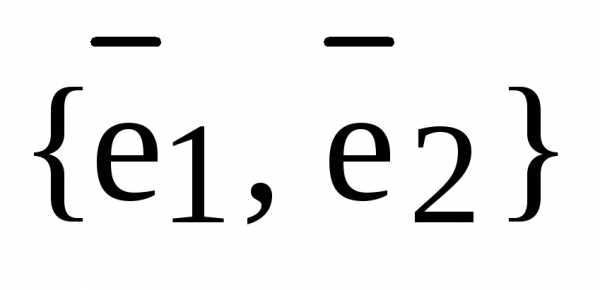 – базис
– базис  и
и 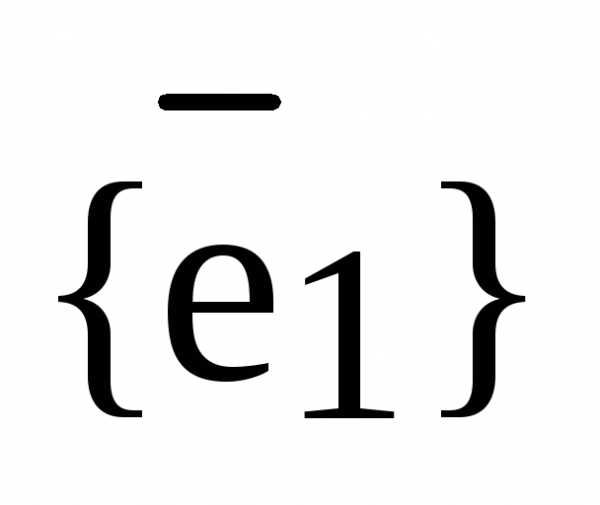 – базис
– базис  . Тогда , и
. Тогда , и  , .
, .
Таким образом, любой вектор прямой L, плоскости Р и пространства S можно разложить по базису  :
:
.
Обозначение. В силу теоремы о равенстве векторов, мы можем отождествить любой вектор с упорядоченной тройкой действительных чисел и писать:
.
Это возможно лишь том случае, когда базис  фиксирован и нет опасности спутаться.
фиксирован и нет опасности спутаться.
Определение. Запись вектора в виде упорядоченной тройки действительных чисел называют координатной формой записи вектора: .
п.4. Линейные операции с векторами в координатной форме записи.
Пусть 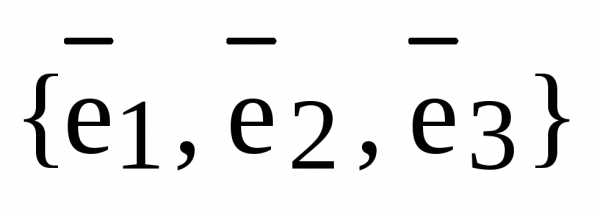 – базис пространства
– базис пространства  и
и 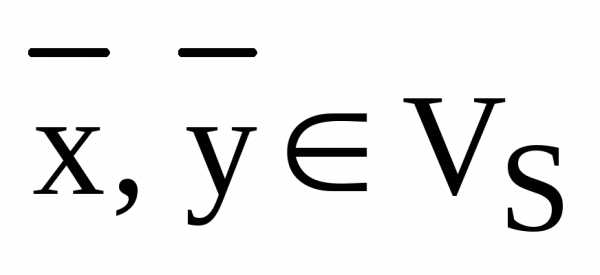 – два его произвольных вектора. Пусть и – запись этих векторов в координатной форме. Пусть, далее,
– два его произвольных вектора. Пусть и – запись этих векторов в координатной форме. Пусть, далее, 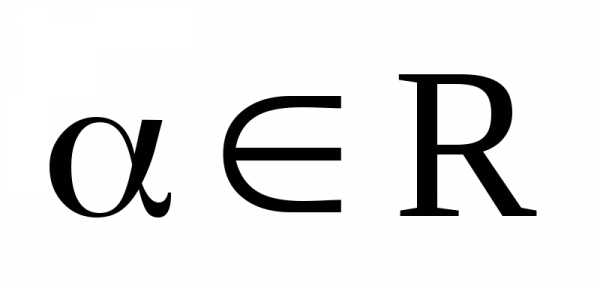 – произвольное действительное число. В этих обозначениях имеет место следующая теорема.
– произвольное действительное число. В этих обозначениях имеет место следующая теорема.
Теорема. (О линейных операциях с векторами в координатной форме.)
1) ;
2) .
Другими словами, для того, чтобы сложить два вектора нужно сложить их соответствующие координаты, а чтобы умножить вектор на число, нужно каждую координату данного вектора умножить на данное число.
Доказательство. Так как по условию теоремы , , то используя аксиомы векторного пространства, которым подчиняются операции сложения векторов и умножения вектора на число, получаем:
.
Отсюда следует .
Аналогично доказывается второе равенство.
Теорема доказана.
п.5. Ортогональные векторы. Ортонормированный базис.
Определение. Два вектора называются ортогональными, если угол между ними равен прямому углу, т.е.  .
.
Обозначение: 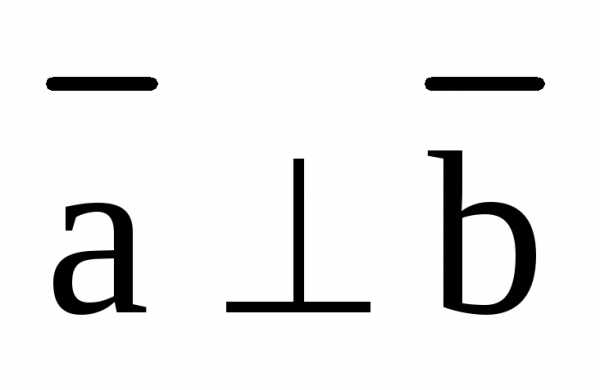 – векторы
– векторы  и
и 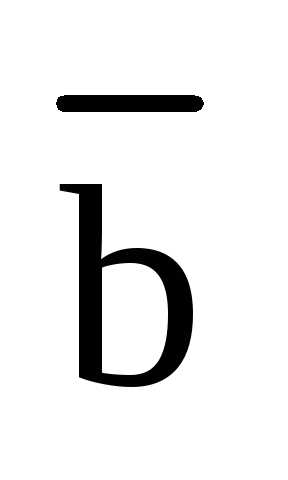 ортогональны.
ортогональны.
Определение. Тройка векторов 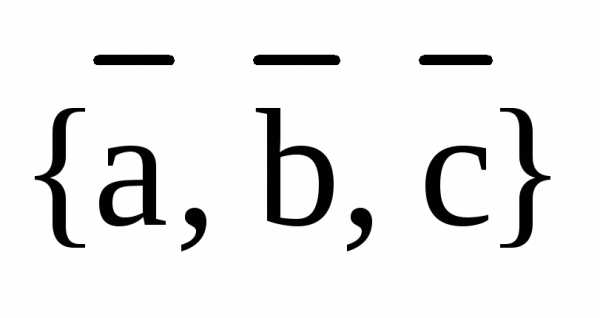 называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е.
называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е. 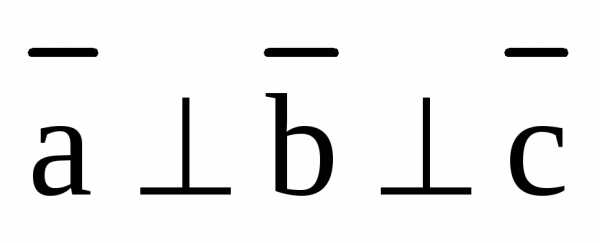 ,
, 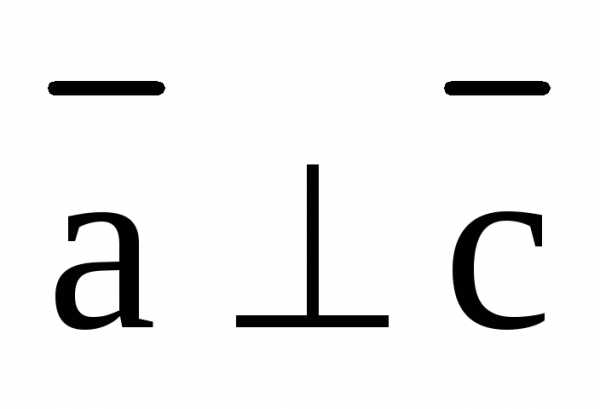 .
.
Определение. Тройка векторов 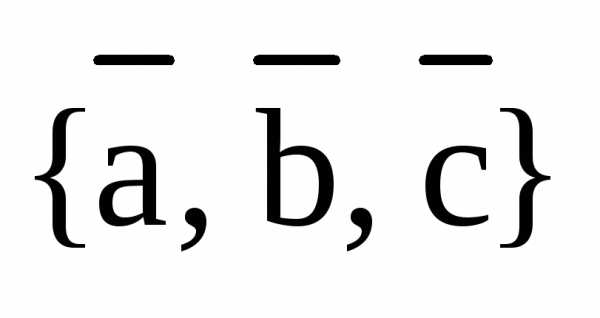 называется ортонормированной, если она ортогональная и длины всех векторов равны единице: .
называется ортонормированной, если она ортогональная и длины всех векторов равны единице: .
Замечание. Из определения следует, что ортогональная и, следовательно, ортонормированная тройка векторов является некомпланарной.
Определение. Упорядоченная некомпланарная тройка векторов 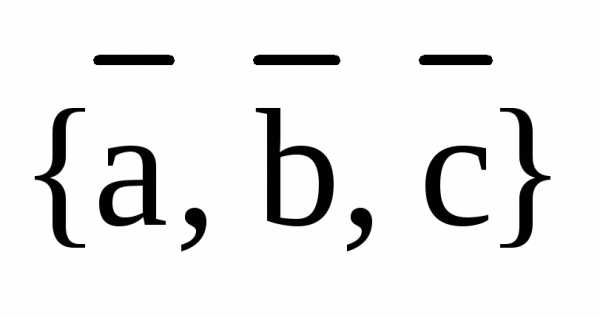 , отложенных от одной точки, называется правой (правоориентированной), если при наблюдении с конца третьего вектора
, отложенных от одной точки, называется правой (правоориентированной), если при наблюдении с конца третьего вектора  на плоскость, в которой лежат первые два вектора
на плоскость, в которой лежат первые два вектора  и
и  , кратчайший поворот первого вектора
, кратчайший поворот первого вектора  ко второму
ко второму  происходит против часовой стрелки. В противном случае тройка векторов называется левой (левоориентированной).
происходит против часовой стрелки. В противном случае тройка векторов называется левой (левоориентированной).
рис.6.
Здесь, на рис.6 изображена правая тройка векторов 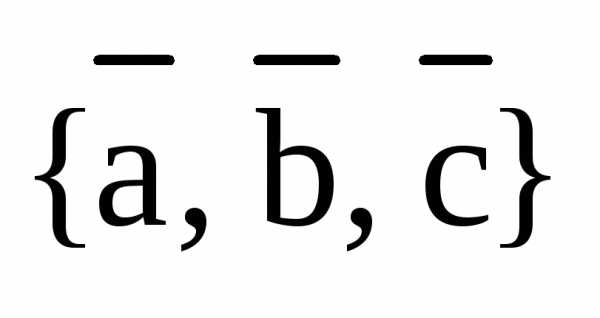 . На следующем рис.7 изображена левая тройка векторов
. На следующем рис.7 изображена левая тройка векторов 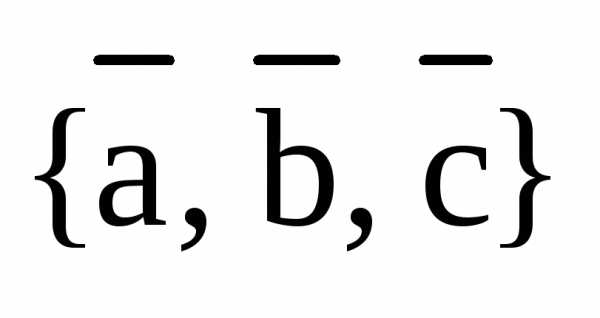 :
:
рис.7.
Определение. Базис 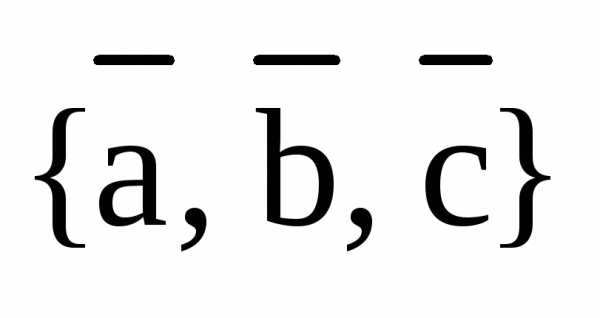 векторного пространства
векторного пространства  называется ортонормированным, если
называется ортонормированным, если 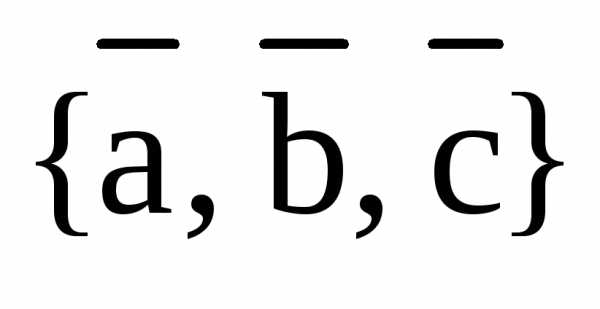 ортонормированная тройка векторов.
ортонормированная тройка векторов.
Обозначение. В дальнейшем мы будем пользоваться правым ортонормированным базисом 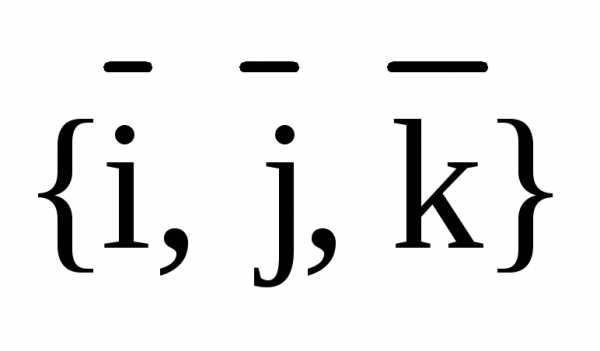 , см. следующий рисунок:
, см. следующий рисунок:
рис.9.
Любой вектор можно разложить по этому базису: