Замкнутая линия что это такое

Замкнутые и незамкнутые линии. Видеоурок. Математика 1 Класс

На этом уроке мы познакомимся с понятиями «замкнутая линия» и «незамкнутая линия», научимся их различать и строить. Также рассмотрим такие понятия, как «звенья» и «вершины» кривой линии. В дальнейшем эти знания будем использовать для решения более сложных задач.

Тема: Знакомство с основными понятиями

Урок: Замкнутые и незамкнутые линии

Задание 1

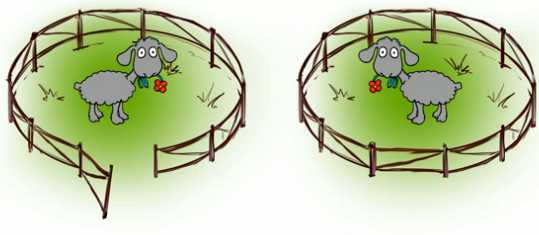
На данном рисунке видим, что овечке легче будет выбраться из первой ограды, потому что она открыта – незамкнутая. Из-за второй ограды будет выйти сложнее, так как она закрыта. Начертим линии, которые будут соответствовать первой и второй ограде.

Итак, мы получили две линии, из которых первая замкнутая, а вторая незамкнутая.

Задание 2: Определить, какие линии на рис. 3 замкнутые, а какие незамкнутые.

На рисунке видим, что линии № 1, 3, 6 – это незамкнутые линии. Для того чтобы сомкнуть эти линии, достаточно соединить концы линий вместе. Получим:

Итак, линия, концы которой не соединены вместе, называется незамкнутой линией. Линия, концы которой соединены вместе, называется замкнутой линией.

Каждая ломаная линия состоит из нескольких отрезков – звеньев. Звенья ломаной не лежат на одной прямой. Конец одного звена является началом другого. Место, где соединяются два звена, а также концы разомкнутой ломаной, называется вершиной.

Итак, на данном уроке мы познакомились с понятиями «замкнутая линия» и «незамкнутая линия». Мы научились их строить, а также применять знания на практике для построения таких линий.

Список литературы

Александрова Л.А., Мордкович А.Г. Математика 1 класс. – М: Мнемозина, 2012.
Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.

Беденко М.В. Математика. 1 класс. – М7: Русское слово, 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Фестиваль педагогических идей (Источник).

2. Социальная сеть работников образования (Источник).

3. Фестиваль педагогических идей (Источник).

Домашнее задание

1. Определить, какие линии изображены на рисунке.

2. Определить количество звеньев каждой линии.

3. Определить количество вершин каждой линии.

4. Построить незамкнутую линию, у которой 4 вершины.

5. Построить замкнутую линию, у которой 6 звеньев.

Линии: прямая, кривая, ломаная. Замкнутые и незамкнутые линии

Линия – это геометрическая фигура, образованная множеством точек, последовательно расположенных друг за другом.

Любую линию можно представить как след от точки, перемещающейся по данному пути. Например, грифель карандаша при прикосновении к бумаге оставляет на ней точку (1), но если грифелем провести по бумаге, то получится линия – последовательность точек, расположенных друг за другом (2):

Геометрические линии не имеют толщины.

Виды линий

Геометрические линии делятся на три вида:

Линия	Пример
Прямая
Ломаная
Кривая

Замкнутые и незамкнутые линии

Ломаные линии и кривые линии могут быть как замкнутыми, так и незамкнутыми. Замкнутая линия – это линия, у которой начало совпадает с концом (концы соединены друг с другом).

Самой простой геометрической фигурой, образованной замкнутой ломаной линией, является треугольник:

Все остальные многоугольники (четырёхугольник, пятиугольник, шестиугольник и т. д.) тоже являются замкнутыми ломаными линиями.

Самым распространённым примером замкнутой кривой линии является окружность:

Незамкнутая линия – это линия, у которой конец не совпадает с началом (концы линии не соединены друг с другом):

звенья, вершины, длина. Замкнутая ломаная

Ломаная линия – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков – вершинами ломаной.

Построим ломаную из четырёх отрезков:

Отрезки AB, BC, CD и DE – это звенья ломаной. Точки A, B, C, D и E – вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA.

Замкнутая ломаная

Если концы ломаной совпадают, то такая ломаная называется замкнутой:

ломаная ABCDE.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник ABCED.

Длина ломаной

Длина ломаной – это сумма длин всех её звеньев.

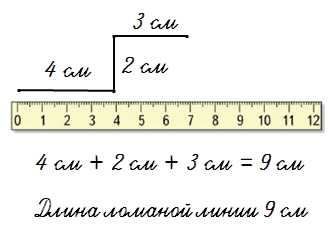
Найдём длину ломаной, сложив длины всех её звеньев:

ABCD = AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

Ломаная линия / Виды линий / Справочник по математике для начальной школы

Главная
Справочники
Справочник по математике для начальной школы
Виды линий
Ломаная линия

Ломаная линия состоит из отрезков - звеньев.

Конец одного отрезка - начало другого. Никакие два соседние звена не лежат на одной прямой.

Концы каждого звена - это вершины. Их можно обозначать буквами.

Ломаная линия бывает незамкнутая.

Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.

Такая замкнутая ломаная линия называется треугольником.

У нее три вершины.

У треугольника три звена.

Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.

Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.

Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.

Например,

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точка. Кривая. Прямая линия

Отрезок. Луч

Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине

Виды линий

Правило встречается в следующих упражнениях:

1 класс

Страница 43, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 71, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 78, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 124, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 17, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 34, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 13. Вариант 2. № 3, Волкова, Проверочные работы

Страница 41, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 84, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 36, Моро, Волкова, Рабочая тетрадь, 2 часть

2 класс

Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Задание 31, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 24. Тест 1. Вариант 1, Моро, Волкова, Проверочные работы

Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 16, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 27, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 59, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 37, Моро, Волкова, Рабочая тетрадь, 2 часть

3 класс

Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 41, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 108, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 5, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 61, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 6. Вариант 1. № 2, Моро, Волкова, Проверочные работы

Страница 7. Вариант 2. № 2, Моро, Волкова, Проверочные работы

Страница 35, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 75, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

4 класс

Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Пользовательское соглашение

Замкнутая ломаная линия — как она выглядит, и что такое вершины ломаной

Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.

Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:

Картография — для построения изображений улиц и схем маршрутов.
Архитектура — очертания зданий и строений.
Ландшафтный дизайн — декоративное оформление и расположение тропинок.
Химия — молекулярная структура сложных полимерных соединений.
Медицина — мониторы для контроля функционального состояния органов и систем.

Типы ломаных линий

Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.

Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.

Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.

Всего существует 4 типа подобных линий по своей структуре:

Замкнутые, которые не имеют пересечений.
Незамкнутые, которые не имеют пересечений.
Незамкнутые самопересекающиеся.
Замкнутые, имеющие самопересечения.

Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.

Особенности замкнутых линий

Рассмотрим подробнее составляющие части этой геометрической фигуры.

Один отрезок из тех, что составляют описываемую фигуру, называется ее звеном. Ломаной может считаться такая линия, которую составляют как минимум два отрезка — звена. Если звено одно — это просто единичный отрезок.
Существует также понятие вершины ломаной. Этим термином принято называть точку, в которой соединяются концы двух звеньев. Такие точки в геометрии принято обозначать с помощью заглавных латинских букв. Сама ломаная называется сочетанием обозначений этих вершин. Например, названием такой линии может послужить сочетание ABCDEF.
Если концы крайних звеньев этого геометрического объекта соединяются в одной точке, такая линия называется замкнутой.
Ломаная линия может пересекать саму себя.
Конечные вершины такой фигуры в геометрии принято называть черными точками.

Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.

Многоугольник как разновидность замкнутой ломаной

Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.

Если вершины принадлежат одной и той же стороне многоугольника — они носят название смежных.
Если отрезок соединяет две любых вершины, не являющиеся смежными, он называется диагональю.
Если у многоугольника имеется n вершин — он называется n-угольником. У такой фигуры имеется количество сторон, равное n.
Такая ломаная делит плоскость на 2 части — внешнюю и внутреннюю.
Если точки многоугольника лежат по одну сторону от прямой и проходят через 2 соседние вершины — его принято называть выпуклым.
Угол выпуклого многоугольника при данной вершине — это угол, который образован двумя его сторонами, для которых эта вершина является общей.
Внешний угол выпуклого многоугольника при определенной вершине — это угол, смежный с внутренним углом многоугольника при этой же самой вершине.

Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.

Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.

Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.

У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.

Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.

Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.

Ломаная — Википедия

Материал из Википедии — свободной энциклопедии

Ломаная A₁A₂A₃A₄A₅A₆

Ло́маная, ломаная линия — геометрическая фигура, состоящая из отрезков, последовательно соединённых своими концами.

Ломаной (ломаной линией) A1A2…An{\displaystyle A_{1}A_{2}\dots A_{n}} называется фигура, которая состоит из отрезков [A1A2]{\displaystyle [A_{1}A_{2}]}, [A2A3]{\displaystyle [A_{2}A_{3}]}, …, [An−1An]{\displaystyle [A_{n-1}A_{n}]}.

Точки A1{\displaystyle A_{1}}, …An{\displaystyle A_{n}}, называются вершинами ломаной, а отрезки [A1A2]{\displaystyle [A_{1}A_{2}]}, [A2A3]{\displaystyle [A_{2}A_{3}]}, …, [An−1An]{\displaystyle [A_{n-1}A_{n}]} — звеньями ломаной.

Ломаная называется невырожденной, если для любого k∈{1,2,…,n−2}{\displaystyle k\in \{1,2,\dots ,n-2\}} отрезки [AkAk+1]{\displaystyle [A_{k}A_{k+1}]} и [Ak+1Ak+2]{\displaystyle [A_{k+1}A_{k+2}]} не лежат на одной прямой; в противном случае — вырожденной.

Ломаная имеет самопересечение, если хотя бы два её звена имеют общую точку помимо общей вершины:

Изображённую здесь ломаную следует называть «ломаная A₁A₂A₃A₄A₅A₆».

Ломаная называется замкнутой, если первая и последняя точки ломаной совпадают; в этом случае дополнительно требуют, чтобы отрезки A1A2{\displaystyle A_{1}A_{2}} и An−1An{\displaystyle A_{n-1}A_{n}} также не лежали на одной прямой:

Замкнутую плоскую ломаную часто называют многоугольником: в этом случае изображённая ломаная A₁A₂A₃A₄A₅A₁ будет называться «многоугольник» A₁A₂A₃A₄A₅», а звенья будут называться сторонами многоугольника. В ряде случаев, например, при рассмотрении многогранников, стороны многоугольника называются рёбрами.

Ломаная линия ℹ️ определение, виды, теоремы, примеры построения замкнутых и незамкнутых геометрических фигур, вершины и звенья

Краткое описание

Специалисты называют ломаной ту геометрическую фигуру, которая представляет собой непрямую линию, состоящую исключительно из многочисленных соединённых отрезков. Учащимся нужно запомнить, что все эти фрагменты могут сходиться под абсолютно разными углами. Проще говоря, если есть даже самый маленький угол между двумя соединёнными отрезками, то это линия своеобразного ломаного типа.

Прямая тоже может состоять сразу из нескольких геометрических фрагментов, но угол их соединения приравнивается к нулю. Для избежания грубых математических ошибок нужно помнить, что ломаная линия отличается от кривой, так как отдельные отрезки представляют собой прямую линию, чего нельзя сказать о кривой.

В некоторых случаях пространственная ломаная может образовывать замкнутую фигуру. Но такая ситуация возможна только тогда, когда концы крайних отрезков совпадают, а также пересекают самих себя. Рассматриваемая в математике фигура состоит из вершин и отрезков, которые и соединяют эти вершины. Но в этом случае действует правило — два последних отрезка не должны лежать на одной прямой.

Сторонами или звеньями изогнутой линии принято называть составные отрезки. Минимальное количество звеньев — два. Специалисты привыкли называть чёрными точками конечные вершины ломаной линии. Чтобы графически всё выглядело правильно, необходимо использовать обозначения в соответствии с названиями задействованных вершин.

Если конечные вершины совпадают, тогда речь касается изогнутой замкнутой линии. В качестве примера можно рассмотреть многоугольник. Эта фигура представляет собой плоскую замкнутую ломаную, которая лишена каких-либо самопересечений. Вершины ломаной линии и её звенья относятся к многоугольнику. Если речь касается фигуры с тремя сторонами и вершинами, то это треугольник.

Немного сложнее разобраться с замкнутой ломаной и её четырьмя сторонами, так как это может быть прямоугольник, квадрат, параллелограмм, ромб и даже трапеция. Если фигура имеет пять или более сторон, то она называется n-угольником. Символ n указывает на точное число вершин.

Некоторые математические примеры касаются изогнутой линии с самопересечениями (пятиконечная звезда). К этой категории также можно отнести зигзаг, в котором каждый второй отрезок параллелен другому, а последние формируют одинаковый угол.

Математическое определение

Ломанной принято называть ту геометрическую фигуру, которая состоит из обычных отрезков (R1, R2, R3 и R4, Rn-1 Rn). Вершинами изогнутой принято называть точки R1…Rn, а вот все остальные отрезки — это неотъемлемые звенья. Если для любого w действует формула {1, 2, n — 2}, а отрезки не расположены на одной прямой, то такая ломанная будет называться невырожденной. В противном случае придётся иметь дело с вырожденным примером.

Для лучшего усвоения этой темы следует рассмотреть несколько примеров. Изогнутая может иметь самопересечение, но это возможно только в том случае, если минимум два отрезка обладают общей точкой (за исключением вершины).

В математике часто можно встретить фигуру, которая является обычной ломаной линией. В этом случае практикуется применение следующей записи: R1R2R3R4R5R6. Если ученику предстоит разобраться со всеми нюансами построения замкнутой ломаной из трёх звеньев и более, тогда ему понадобятся вспомогательные отрезки (к примеру: R1, R2, а также Rn -1 Rn, которые не должны лежать на одной прямой).

Замкнутую плоскую ломаную линию принято называть многоугольником. Если рассматривать многогранники, то все стороны фигуры будут называться рёбрами. Учителя России предпочитают создавать краткосрочное планирование по этой теме, так как в этом случае можно донести больше полезной информации до учеников.

Гораздо проще разобраться с изгибами зигзага, так как они используются в швейном деле, в распространённом декоративном оформлении предметов обихода в качестве орнамента. Стоит отметить, что изогнутая линия нашла широкое применение в различных отраслях:

Архитектура. Изогнутые линии позволяют сооружать интересные номера.
Картография (тщательное проектирование маршрутов и подробное схематическое изображение всех улиц).
Химическая отрасль (различные соединения и своеобразные молекулярные структуры).
Востребованный дизайн ландшафтов (утончённое оформление, расположение дорожек).
Медицина (мониторы для наблюдения за сердечным ритмом).
Метод освоения каллиграфических навыков в китайском языке.

Изучение этой темы в математике является обязательным, так как от этого зависит качество усвоения материала учеником.

Основные разновидности ломаных

Геометрическая фигура может быть построена совершенно по любому из действующих методов. Специалисты выделяют замкнутую, а также незамкнутую ломанную. Повышенное внимание уделяют самопересекающимся, непересекающимся линиям. Классическая замкнутая ломаная является многоугольником. В математике самопересекающейся принято называть ту линию, отрезки которой имеют минимум одно пересечение. По своей структуре ломаная может быть весьма разнообразной, из-за чего нужно внимательно относиться ко всем аспектам.

В начальных классах школы принято рассматривать следующий пример: ломаная включает в себя сразу пять звеньев либо сторон: ZX, XC, CV, VB, BN. Та точка, где неизбежно соединяются два звена, называется вершиной. В этом случае имеется сразу четыре вершины: X, С, V, B.

Повышенное внимание нужно уделить изучению звена ломаной. Звеньями эксперты привыкли называть стороны либо отрезки, из которых образована линия. Всего одно такое звено может быть рассмотрено только в качестве отрезка. А вот для построения ломаной необходимо задействовать как минимум два звена. Вершины — это классические точки, которые представляют собой концы одних отрезков ломаной. Обозначить точки можно только латинскими буквами.

Пример замкнутой, а также традиционной незамкнутой ломаной линии, которую часто можно встретить в геометрии и алгебре:

Если необходимо определить точную длину ломаной, то для этого следует поочерёдно сложить все известные данные задействованных звеньев (ZX + XC + CV + VB + BN).

Базовые понятия

Чтобы гарантировано освоить все правила, которые касаются использования изогнутой линии в математике, необходимо разобраться со звеньями. Существует ряд нюансов, которые можно сопоставить с элементарной геометрической конструкцией. Линию формируют отдельные отрезки, которые в математике называются звеньями. Если все концы ломаной соединяются в одной точке, то такая фигура будет называться замкнутой.

Все задействованные звенья могут обладать взаимными пересечениями. Вершинами специалисты привыкли называть точки соединения отрезков. О многоугольнике можно говорить только в том случае, если звенья не пересекаются между собой. Звено обозначают сразу двумя латинскими буквами. Каждая вершина изогнутой линии может обозначаться только одной буквой. Только тщательное изучение всех правил и нюансов позволит правильно решать математические задачи.

Особенности построения многоугольников

В этом случае речь касается геометрической фигуры, отличающейся итоговым количеством звеньев, углов. Последние могут быть сформированы только несколькими звеньями замкнутой ломаной, которые сходятся в одной точке. Задействованные звенья также могут носить логическое название сторон многоугольника. Общие точки двух отрезков называются вершинами. Стоит учесть, что количество сторон либо звеньев в каждой такой фигуре в точности соответствует количеству углов. Если задействовать замкнутую ломаную из трёх отрезков, то в итоге получится треугольник.

Абсолютно все многоугольники обладают одинаковыми свойствами. Самая маленькая фигура включает в себя всего три стороны. Но расположенные в непосредственной близости треугольники могут формировать совершенно новые фигуры. Если имеющиеся вершины изучаемого многоугольника являются своеобразным дополнением одной стороны, то их всегда называют соседними.

Когда многоугольник был расположен относительно одной прямой в любой плоскости, то она называется выпуклой. А вот прямая может содержать в себе одну сторону фигуры и принадлежать полуплоскости. Если отрезок соединяет не соседние вершины, то он называется диагональю. Смежный внутренний угол при некоторой вершине называется внешним.

Следует отметить тот факт, что когда все имеющиеся углы и стороны многоугольника равны между собой, то речь касается правильных отрезков. Каждая геометрическая фигура обладает определёнными параметрами. Треугольниками в алгебре принято называть обычную плоскую фигуру, которая состоит из трёх точек, не расположенных на одной прямой. Для соединения используются обычные отрезки. Точки выступают в роли вершин треугольника. Такая фигура имеет всего три угла. Специалисты различают 6 разновидностей треугольников:

Элементарные разносторонние. В этом случае каждая следующая сторона отличается своей длиной.
Равносторонние. Абсолютно все стороны обладают идентичной длиной.
Специфические остроугольные. Сформированные углы имеют острую форму.
Универсальные равнобедренные. Сразу две стороны из трёх существующих обладают одинаковой длиной.
Тупоугольные. Фигура обладает одним тупым углом.
Традиционные прямоугольные. Нарисованная фигура должна иметь минимум один прямой угол.

Четырёхугольником называют ту конструкцию, которая обладает четырьмя сторонами и четырьмя сторонами. Использование таких геометрических фигур обладает определёнными нюансами.

Ключевые нюансы

Существует две линии SWT и SFT одинаковой толщины, которые соединяют свободные концы одной прямой ST. В итоге образуется ломаная. Изогнутая SFT именуется внутренней ломаной, а вот SWT внешней. В качестве примера лучше всего рассмотреть фигуру, которая соответствует математической теореме, что внешняя изогнутая превышает внутреннюю.

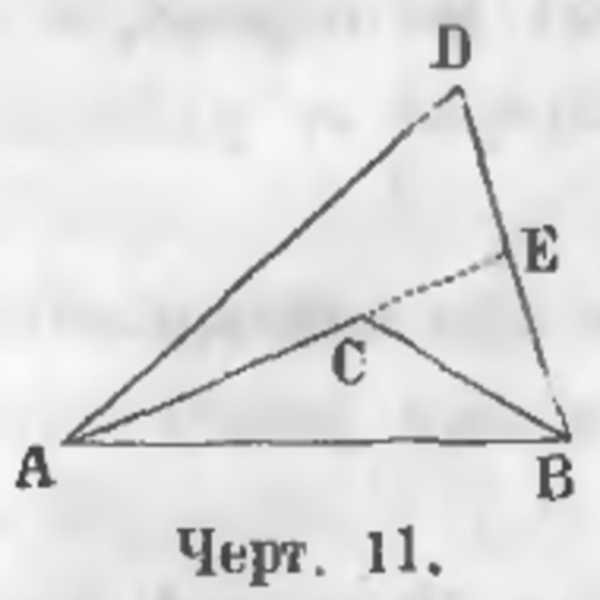
По условиям задачи были даны две ломаные: внутренняя SFT и внешняя SWT. Необходимо доказать, что SWT больше SFT. Для решения этой задачи нужно продолжить линию SF до пересечения с отрезком WT в точке Е. Линия SWE как ломаная гораздо больше прямой SE. Ломанная FET больше имеющейся прямой FT. Если сложить между собой все эти неравенства, то в итоге можно получить: SW+ WE + FE + ET > SF + FE + FT.

Для получения достоверного результата нужно вычесть из обеих частей неравенства по СЕ:

SW+ WE + ET > SF + FT.
WE + ET = WT.

Необходимо рассмотреть и вторую теорему, в соответствии с которой итоговая сумма пересекающихся изогнутых линий больше не пересекающихся. По условиям задачи были даны обычные пересекающиеся ломаные HLK и HRK, а также HR, LK и пересекающиеся части. Решение выглядит следующим образом: неравенства отрезков вытекают из того, что ломаная HEL гораздо больше прямой HL, а вот координаты KER превышают KR.

Нелишним также будет научиться находить общую меру сразу двух линий при помощи линейки. Это правило обязательно осваивают в начальных классах. Для поиска неизвестной общей меры обязательно нужно на большую линию наложить меньшую, потом первый остаток на меньший отрезок, а второй остаток на первый. Все эти манипуляции повторяют ровно до тех пор, пока самый последний остаток максимально не уложится в предпоследнем выполненном действии. Измерение линий всегда означает то, что учащемуся необходимо отыскать её отношение к другим отрезкам, принятым за единицу. Полученное значение называют длиной этой линии, которая может выражаться исключительно в каких-нибудь единицах.

Изучение ломаных линий очень важно, так как они окружают человека повсюду. Речь касается прямых линий, которые меняют своё первоначальное направление, замыкаются, а также пересекаются.

Точка, линия, прямая, луч, отрезок, ломанная

Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

точка A, точка B, точка C

ABC

точка 1, точка 2, точка 3

123

Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие? AAA

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Обозначается строчными (маленькими) латинскими буквами

линия a, линия b, линия c

abc

Линия может быть

замкнутой, если её начало и конец находятся в одной точке,
разомкнутой, если её начало и конец не соединены

замкнутые линии

разомкнутые линии

Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.

самопересекающейся
без самопересечений

самопересекающиеся линии

линии без самопересечений

прямой
ломанной
кривой

прямые линии

ломанные линии

кривые линии

Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны

Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой

прямая линия a

прямая линия AB

Прямые могут быть

пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
параллельными, если не пересекаются, не имеют общей точки.

параллельные линии

пересекающиеся линии

перпендикулярные линии

Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону

У луча света на картинке начальной точкой является солнце

солнышко

Точка разделяет прямую на две части — два луча A A

Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче

луч a

луч AB

Лучи совпадают, если

расположены на одной и той же прямой,
начинаются в одной точке,
направлены в одну сторону

лучи AB и AC совпадают

лучи CB и CA совпадают

CBA

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками

Через одну точку можно провести любое число линий, в том числе прямых

Через две точки — неограниченное количество кривых, но только одну прямую

кривые линии, проходящие через две точки

прямая линия AB

От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ BA✂

Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок

отрезок AB

Задача: где прямая, луч, отрезок, кривая?

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°

Длинный отрезок «поломали» на несколько коротких

Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.

Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.

Обозначается ломанная перечислением всех её вершин.

ломанная линия ABCDE

вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E

звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE

звено AB и звено BC являются смежными

звено BC и звено CD являются смежными

звено CD и звено DE являются смежными

ABCDE646212752

Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305

Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.

Многоугольник — это замкнутая ломанная линия

Стороны многоугольника (помогут запомнить выражения: "пойти на все четыре стороны", "бежать в сторону дома", "с какой стороны стола сядешь?") — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.

Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.

Обозначается многоугольник перечислением всех его вершин.

замкнутая ломанная линия, не имеющая самопересечения, ABCDEF

многоугольник ABCDEF

вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F

вершина A и вершина B являются соседними

вершина B и вершина C являются соседними

вершина C и вершина D являются соседними

вершина D и вершина E являются соседними

вершина E и вершина F являются соседними

вершина F и вершина A являются соседними

сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF

сторона AB и сторона BC являются смежными

сторона BC и сторона CD являются смежными

сторона CD и сторона DE являются смежными

сторона DE и сторона EF являются смежными

сторона EF и сторона FA являются смежными

ABCDEF120605812298141

Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599

Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.д.

треугольники

четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция

пятиугольники

Звенья ломаной линии что это такое

Ломаная линия

Замкнутая ломаная
Длина ломаной

Ломаная линия – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков – вершинами ломаной.

Построим ломаную из четырёх отрезков:

Отрезки AB, BC, CD и DE – это звенья ломаной. Точки A, B, C, D и E – вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA.

Если концы ломаной совпадают, то такая ломаная называется замкнутой:

ломаная ABCDE.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник ABCED.

Длина ломаной

Длина ломаной – это сумма длин всех её звеньев.

Найдём длину ломаной, сложив длины всех её звеньев:

ABCD = AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

naobumium.info

Ломаная линия

Ломаная линия состоит из отрезков - звеньев.

Конец одного отрезка - начало другого. Никакие два соседние звена не лежат на одной прямой.

Концы каждого звена - это вершины. Их можно обозначать буквами.

Ломаная линия бывает незамкнутая.

Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.

Такая замкнутая ломаная линия называется треугольником.

У нее три вершины.

У треугольника три звена.

Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.

Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.

Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.

Например,

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точка. Кривая. Прямая линия

Отрезок. Луч

Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине

Виды линий

Правило встречается в следующих упражнениях:

1 класс

Страница 93, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 101, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 16, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 34, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 13. Вариант 2. № 3, Волкова, Проверочные работы

Страница 25, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 60, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 65, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 107, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 32, Моро, Волкова, Рабочая тетрадь, 2 часть

2 класс

Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 32, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 33. Вариант 2. № 3, Моро, Волкова, Проверочные работы

Страница 50. Вариант 1. Тест, Моро, Волкова, Проверочные работы

Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 16, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 42, Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 78, Моро, Волкова, Рабочая тетрадь, 2 часть

3 класс

Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 6, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 14, Моро, Волкова, Степанова,

Линии. Прямая, кривая, замкнутая, незамкнутая

Акмолдинская область

Г.Кокшетау

КГУ Средняя школа №17

Тема: «Линии. Прямая, кривая, замкнутая, незамкнутая».

Подготовила: Айткожина Ш. Ж.

2015-2016 учебный год

Разработка урока по математике

В 1 «З» классе

Тема: «Линии. Прямая, кривая, замкнутая, незамкнутая».

Цель: познакомить с понятиями линии, прямая, кривая, замкнутая и незамкнутая;

Задачи:

обучающая: сформировать представление о понятиях «линии, прямая, кривая, замкнутая и незамкнута»;

развивающая: развитие вычислительных навыков; творческих познавательных способностей, логическое мышление, воображение, наблюдение.

Воспитывающая: воспитывать интерес к предмету, доброжелательное отношение к учебе.

Оборудование:

У учащихся: 5 одинаковых бумажных полосок; двусторонние листы бумаги с зеленой и желтой сторонами; карточки с числами от 1 до 10; рабочая тетрадь № 1; учебник «Математика 1 класс»;

У учителя: картинки с изображением Вини_Пуха, Совы, Пятачка, ослика Иа, «Дерево настроения». Диск с мелодией песни «Вини-Пух и его друзья»(сл. Б. Заходера, муз. М. Вайнберга).

Ход урока.

І. Организационный момент.

- Вспомним правила поведения на уроке.

Слушай внимательно,

Объясняй обстоятельно.

Ответить хочешь – не шуми,

А только руку подними.

- Будьте внимательными и любознательными, ведь знания сегодня вы будете добывать сами, хотя мы не сможем обойтись без повторения того, что вам знакомо.

ІІ. Актуализация знаний.

(Звучит песня «Вини-Пух и его друзья»).

- Какой сказочный герой поет эту песню? Он и его друзья помогут нам сегодня на уроке. Вместе с Вини-Пухом мы отправляемся к мудрой Сове за темой урока. По дороге вас ждут задания. Приготовьте карточки для устного счета.

1. Учитель открывает доску, на которой изображен маршрут (в виде разных линий), по которому будут двигаться ученики, выполняя задания. На доске также написано тема урока, но она закрыта от учеников.

- Сначала Винни-Пух пошел по дорожке.

(Учитель показывает на доске рисунок и прикрепляет изображение Винни-Пух).

4-2 3-1 8+1

2+3 5+1 6+1 9-1

(Учащиеся вычисляют значения выражений и показывают карточки с числами 5. 2, 6, 2, 7, 9 , 8).

2. Учитель прикрепляет изображения ослика Иа.

- Вини- Пух пришел к озеру.

-Кого он встретил тут? (Ослика Иа).

-Ослик смотрел в озеро и вспомнил состав числа 5.

(Ученики вспоминают состав числа 5.Учитель прикрепляет к середине озеро карточки с выражениями 4+1, 3+2, 1+4, 0+5).

3. Винни-Пух пошел дальше и навестил своего друга Пятачка, который придумал задачи в стихах. Решите их и покажите ответы карточками.

(Учитель прикрепляет на доске изображение Пятачка и рисунок).

1.Дружно муравьи живут 2. В хоре семь кузнечиков

И без дела не снуют: Песни распевали.

Сколько муравьев не Вскоре пять кузнечиков

Два несут былинку, Голос потеряли.

Три несут иголки. Сосчитай без лишних слов-

Сколько всех под елкой? Сколько петь осталось голосов?

3. Сколько маленьких утят

Плавать и нырять хотят?

Три утенка далеко,

Два нырнули глубоко.

Сколько их всего в пруду?

Сосчитать я не могу?

4. Винни-Пух дошел по дорожке до домика Совы. Она спит, но во сне что-то говорит. Может быть, она считает в уме?

Творческая деятельность.- Ребята, подумайте и скажите, о чем может во сне говорить Сова?

Игра «День -ночь».

- Я говорю примеры, вы их решаете и говорите окончательный ответ: 7-5+1=

4+1+2=

10-1-1-1=

9+0+1-2-1=

-Покажите правильный ответ.

-Сова проснулась и предлагает вам сделать зарядку вместе с ней.

ІІІ. Физкультминутка.

Раз, два, три, четыре, пять!

Все мы можем посчитать.

Голову поднимем выше

И легко-легко подышим,

Потянулись на носочках столько раз,

Сколько пальцев на руке у вас.

Раз, два, три, четыре, пять!

Ходим на месте.

Прибавляем, вычитаем,

Математику мы знаем.

ІV. Постановка проблемы и поиск выхода из нее.

-Сова просит вас обратить внимание на дорожки, по которым шел Винних-Пух.

- Знакомы ли они вам? (Первая дорожка похожа на не замкнутую линию, вторая – это замкнута линия, третья дорожка тоже, незамкнутая линия).

- Почему вы так решили про третью линию? На какую линию она похоже? ( На первую линию).

- Чем похожа? (Она незамкнутая).

- Чем отличается? (Имеет углы, прямые стороны).

- Как бы вы назвали эту линию?

- Такую линию принято называть ломаной замкнутой.

V. Открытие нового знания. Формулировка темы.

- У вас на столах лежат 5 полосок – моделей отрезков. Постройте из них ступеньки, по которым Винни-Пух смог бы подняться к Сове.

(Дети строят ступеньки на партах. Один ребенок вместе с учителем выполняет задание на доске .

- На какую линию похожи ступеньки? (На замкнутую ломаную).

-Из чего мы ее строили? (Из отрезков).

-Можно ли из этих отрезков построить замкнутую линию? (Да).

-Постройте.

- Какая фигура получилась? (Многоугольник).

- Сколько у него углов? (5).

-Предположите, как называется тема нашего урока.(Линии, прямая, кривая, замкнутая и незамкнутая линии).

VІ. Физкультминутка.

Поднимает руки класс- это раз.

Повернулась голова – это два.

Руки вниз, впереди смотри – это три.

Руки в стороны пошире развернули на четыре.

Самого себя обнять - это пять.

Всем ребятам дружно сесть – это шесть.

Громко крикнуть «А» надо всем – это семь.

А когда мы скажем восемь - значит, тишины попросим.

VІІ. Первичное закрепление.

Работа по учебнику.

-Откройте учебники на странице 18. № 1, №2 .

- Рассмотрите рисунок. – Какие линии вы видите?

- Чем ломанная линия отличается от прямой линии?

№ 3. – Назовите прямые, кривые линии?

Стр. 20 № 4 – Что лишнее?

Письмо в тетради.

- Страница 17, № 1 . – 1. Найдите прямые, кривые, замкнутые и незамкнутые линии. Обведи.

-№ 2. –Раскрась большие фигуры синим цветом, а маленькие – зеленым.

- стр. 18, №3 – Нарисуй пропущенную фигуру. (Треугольник).

(Ученики выполняют задание самостоятельно).

VІІІ. Итог урока.

- С какими линиями мы сегодня познакомились?

- Какими бывают линии?

- Из чего состоят ломаные линии?

-Какие фигуры получают из замкнутых линий?

Мне очень понравился урок, вы хорошо работали, хорошо отвечали, внимательно слушал и.

-Вам было интересно на уроке, вы поняли новую тему?

-На парте у вас лежат двустронние листочки.

- Если вы все поняли, чувствовали себя на уроке комфортно и спокойно, то прикрепите его к доске на наше «Дерево настроения» зеленой стороной, а если вы волновались, не поняли тему – то желтой.

Самоанализ урока математики

Данный урок проводился в 1 классе в первой четверти.

Тема: «Линии. Прямая, кривая, замкнутая, незамкнутая».

Цель: познакомить с понятиями линии, прямая, кривая, замкнутая и незамкнутая;

Задачи:

обучающая: сформировать представление о понятиях «линии, прямая, кривая, замкнутая и незамкнута»;

Воспитывающая: воспитывать интерес к предмету, доброжелательное отношение к учебе.

Оборудование:

Кривая — Википедия

Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.

В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки. Например, в «Началах» Евклида она определялась как «длина без ширины», также иногда её определяли как «границу фигуры».

По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и некоторые трансцендентные кривые), применяя в каждом случае специальные приёмы.

Отображение отрезка[править | править код]

Чаще всего кривая определяется как непрерывное отображение из отрезка в топологическое пространство:

γ:[a,b]→X{\displaystyle \gamma \colon [a,b]\to X}

При этом кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если [a,b]=[0,1]{\displaystyle [a,b]=[0,1]}, путями.

Отношение эквивалентности[править | править код]

Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые

γ1:[a1,b1]→X{\displaystyle \gamma _{1}\colon [a_{1},b_{1}]\to X} и γ2:[a2,b2]→X{\displaystyle \gamma _{2}\colon [a_{2},b_{2}]\to X}

эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) h{\displaystyle h} из отрезка [a1,b1]{\displaystyle [a_{1},b_{1}]} на отрезок [a2,b2]{\displaystyle [a_{2},b_{2}]}, такая что

γ1≡γ2∘h.{\displaystyle \gamma _{1}\equiv \gamma _{2}\circ h.}

Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.

Комментарий[править | править код]

Приведённое определение во многом позволяет передать наше интуитивное представление о кривой как о чём-то, «нарисованном без отрыва карандаша». Однако это определение является слишком слабым, поскольку ему удовлетворяют многие фигуры, которые трудно считать кривыми.

Например, возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат (см. кривая Пеано). Более того, согласно теореме Мазуркевича, любое компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.

Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.

Кривая Жордана[править | править код]

Кривая Жордана на плоскости с положительной мерой Лебега.

Кривой Жордана или простой кривой называется образ непрерывного инъективного отображения (вложения) окружности или отрезка в пространство. В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой.

Известная теорема Жордана утверждает, что любая замкнутая кривая Жордана на плоскости делит её на «внутреннюю» и «внешнюю» часть.

Кривая Жордана является довольно сложным объектом, например, возможно построить плоскую кривую Жордана с ненулевой мерой Лебега, этот пример аналогичен кривой Пеано был построен Осгудом^[1]. .

В математическом анализе часто используется определение гладкой кривой. Определим сначала плоскую кривую (то есть кривую в R2{\displaystyle \mathbb {R} ^{2}}). Пусть x(t){\displaystyle x(t)} и y(t){\displaystyle y(t)} — функции на отрезке [a,b]{\displaystyle [a,b]}, непрерывно дифференцируемые на этом отрезке, и такие, что (x′(t))2+(y′(t))2{\displaystyle (x'(t))^{2}+(y'(t))^{2}} ни для какого t не равно нулю. Тогда отображение γ:[a,b]→R2,t↦(x(t),y(t)){\displaystyle \gamma :[a,b]\to \mathbb {R} ^{2},t\mapsto (x(t),y(t))} задаёт кривую, которая является гладкой; непараметризованная кривая называется гладкой, если она допускает такую параметризацию. Длину гладкой кривой можно вычислить по формуле

L(γ)=∫ab(x′(t))2+(y′(t))2dt.{\displaystyle {\text{L}}(\gamma )=\int _{a}^{b}{\sqrt {(x'(t))^{2}+(y'(t))^{2}}}\,dt.}

Это определение можно обобщить на отображения в другие пространства, а также на отображения другого класса гладкости, см. ниже.

Определение в дифференциальной геометрии[править | править код]

Если X{\displaystyle X} — гладкое многообразие, можно определить гладкую кривую на X{\displaystyle X} как гладкое отображение γ:[a,b]→X{\displaystyle \gamma \colon [a,b]\to X}, дифференциал которого нигде не обращается в нуль. Если класс гладкости многообразия X{\displaystyle X} равен k{\displaystyle k}, то Ck{\displaystyle C_{k}}-кривая вводится как кривая, для которой γ{\displaystyle \gamma } — k{\displaystyle k} раз непрерывно дифференцируемое отображение. Если X{\displaystyle X} — аналитическое многообразие (например, евклидово пространство) и γ{\displaystyle \gamma } — аналитическое отображение, кривую называют аналитической.

Гладкие кривые γ1:I→X{\displaystyle \gamma _{1}\colon I\to X} и γ2:J→X{\displaystyle \gamma _{2}\colon J\to X} называются эквивалентными, если существует диффеоморфизм p:I→J{\displaystyle p\colon I\to J} (замена параметра), такой что γ1=γ2∘p{\displaystyle \gamma _{1}=\gamma _{2}\circ p}. Классы эквивалентности по этому отношению называют непараметризованными гладкими кривыми.

Алгебраические кривые изучаются в алгебраической геометрии. Плоская алгебраическая кривая — это множество точек с координатами x, y, задаваемое множество решений уравнения f(x, y) = 0, где f — многочлен от двух переменных с коэффициентами в поле F. В алгебраической геометрии обычно принимают во внимание не только точки, координаты которых принадлежат F, но и точки с координатами в алгебраическом замыкании F. Если C — плоская алгебраическая кривая, такая что коэффициенты определяющего её многочлена лежат в поле F, она называется кривой, определённой над F. Точки кривой, определённой над F, все координаты которых принадлежат G, называются рациональными над G (или просто G-точками). Пример: кривая x² + y² + 1 = 0, определённая над действительными числами, имеет точки, однако ни одна из них не является действительной точкой.

Алгебраические кривые можно определить и в пространствах большей размерности; они определяются как множество решений системы полиномиальных уравнений.

Любая плоская кривая может быть дополнена до кривой на проективной плоскости. Если плоская кривая определяется многочленом f(x, y) полной степени d, то многочлен

zd⋅f(x/z,y/z){\displaystyle z^{d}\cdot f(x/z,y/z)}

после раскрытия скобок упрощается до однородного многочлена f(x, y, z) степени d. Значения x, y, z, такие что f(x, y, z) = 0 — однородные координаты пополнения плоской кривой, при этом точки исходной кривой — это точки, для которых z не равно нулю. Пример: кривая Ферма xⁿ + yⁿ = zⁿ в аффинной форме принимает вид xⁿ + yⁿ = 1. Процесс перехода от аффинной кривой к проективной можно обобщить и на более высокие размерности.

Часто встречающиеся примеры плоских кривых — коники (кривые второго порядка) и эллиптические кривые, имеющие важные приложения в криптографии. В качестве примеров алгебраических кривых, задаваемых уравнениями более высоких степеней, можно указать следующие:

Трансцендентные кривые — это кривые, не являющиеся алгебраическими. Более точно, трансцендентные кривые — кривые, которые можно задать как линию уровня аналитической, но не алгебраической функции (или, в многомерном случае, системы функций). Примеры трансцендентных кривых:

Типы точек на кривой[править | править код]

Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:

Канторовой кривой называется компактное связное подмножество плоскости такое, что его дополнение всюду плотно.

Важный пример канторовой кривой доставляет ковёр Серпинского. Какова бы ни была канторова кривая L{\displaystyle L}, она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество L′{\displaystyle L'}, гомеоморфное L{\displaystyle L}. Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.

Впоследствии это определение было обобщено Урысоном:

Кривой Урысона называется связное компактное топологическое пространство C{\displaystyle C} топологической размерности 1.

Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.

↑ W. F. Osgood. A Jordan curve of positive area (англ.) // Trans. Am. Math. Soc.. — 1903. — Vol. 4. — P. 107–112.